組合せ

順列では、ものを取り出したときの順番の違いを考えに入れていたが、順番は区別せず取り出したものの区別だけを考えたいことがあり、これを組合せという。順列と同じように、組合せも数が多くなると樹形図を書くのが大変になる。ここでは、組合せの数を計算で求める方法について考えよう。

ボール・箱単射写像全て全射
あり・あり順列重複順列部屋割り
なし・あり組合せ重複組合せ資源配分
あり・なし（右枠の和）部屋割り（区別なし）
なし・なし（右枠の和）資源配分（区別なし）

組合せについて

組合せ$_{n}\text{C}_{r}$の定義

4枚のカード $\fbox{A}$ , $\fbox{B}$ , $\fbox{C}$ , $\fbox{D}$ から 2枚のカードの(順序は考えずに)組をつくる場合の数は，すべて書き出すと

\begin{align} &\left\{\fbox{A},\fbox{B}\right\},\left\{\fbox{A},\fbox{C}\right\},\left\{\fbox{A},\fbox{D}\right\}\\ &,\left\{\fbox{B},\fbox{C}\right\},\left\{\fbox{B},\fbox{D}\right\},\left\{\fbox{C},\fbox{D}\right\} \end{align}

の6通りとなる．これは，順列の考え方を利用し，次のように計算することもできる．

まず，4枚のカードから2枚引いて順列を作ると，樹形図は図のようになり，その総数は $_{4}\mathrm{P}_{2}=4\times3=12$ 通りである．

しかし，2枚のカードの組を作る場合には，図の樹形図で例えば①，②は並ぶ順が異なるだけなので，これらは2つで1通りと数えなければならない． これら以外の順列にも同様のことがいえるので， 2枚のカードの組の総数は，順列の総数 $_{4}\mathrm{P}_{2}$ を2で割ることにより

\begin{align} \dfrac{_{4}\mathrm{P}_{2}}{2}=\dfrac{12}{2}=6 \end{align}

∴6通り

として計算できる．

このようにいくつかの組をつくる場合の数を定義しておこう．

組合せ $_{n}\mathrm{C}_{r}$ の定義

「区別する $n$ 個のものから $r$ 個取り出して作った組」のことを $\boldsymbol{n-r}$ 組合せ(combination)

といい， その組の総数を $\boldsymbol{{n}\mathrm{C}{r}}$ と表す．

この例では， $_{4}\mathrm{C}_{2}=\frac{4\times3}{2}=6$ である．

組合せ$_{n}\text{C}_{r}$の計算

区別する $n$ 個のものから $r$ 個取り出して作る組の総数 $_{n}\mathrm{C}_{r}$ も，先程の例と同じように考えることができる．

まず， $n$ 枚のカードから $r$ 枚引いて順列を作ると，その総数は $_{n}\mathrm{P}_{r}$ 通りある．

順列ではなく， $r$ 枚のカードの組を作る場合には， $n-r$ 順列のうち $r!$ 通りについては同一視することになるので， 順列の総数 $_{n}\mathrm{P}_{r}$ を $r!$ で割ることにより

\begin{align} _{n}\mathrm{C}_{r}=\frac{_{n}\mathrm{P}_{r}}{r!}=&\ \frac{\overbrace{n(n-1)\cdots(n-r+1)}^{r個の積}}{r(r-1)\cdot2\cdot1}\\ =&\ \frac{n!}{(n-r)!r!} \end{align}

$\blacktriangleleft$ 順列 $_{n}\mathrm{P}_{r}$ の計算参照

以上，まとめると

組合せ $_{n}\mathrm{C}_{r}$ の計算

組合せ $_{n}\mathrm{C}_{r}$ は

\begin{align} _{n}\mathrm{C}_{r}=\frac{_{n}\mathrm{P}_{r}}{r!}=&\ \frac{n(n-1)\cdots(n-r+1)}{r(r-1)\cdot2\cdot1}\\ =&\ \frac{n!}{(n-r)!r!} \end{align}

と計算できる．

吹き出し無題

よくあるまちがいとして， $_{n}\mathrm{C}_{0}=0$ としてしまうというのがある． 上の式によれば， $_{n}\mathrm{C}_{0}=\frac{n!}{(n-0)!0!}=1$ である． このことは， $_{n}\mathrm{C}_{0}$ すなわち「区別する $n$ 個のものから0個選ぶ場合の数」は， 「1個も選ばない」という1通りである，と

こじつけ

で覚えてしまうとよい．

組合せの計算練習

次の値を求めよ．

  1. $_{5}\mathrm{C}_{2}$
  2. $_{4}\mathrm{C}_{4}$
  3. $_{10}\mathrm{C}_{3}$
  4. $_{20}\mathrm{C}_{2}$

  1. $_{5}\mathrm{C}_{2}=\dfrac{5\cdot 4}{2\cdot 1}=\boldsymbol{10}$

  2. $_{4}\mathrm{C}_{4}=\dfrac{4\cdot 3\cdot 2\cdot 1}{4\cdot 3\cdot 2\cdot 1}=\boldsymbol{1}$

  3. $_{10}\mathrm{C}_{3}=\dfrac{10\cdot 9\cdot 8}{3\cdot 2\cdot 1}=\boldsymbol{120}$

  4. $_{20}\mathrm{C}_{2}=\dfrac{20\cdot 19}{2\cdot 1}=\boldsymbol{190}$

組合せ〜その1〜

男子が5人，女子が5人いる中で，4人を選ぶ場合の数について以下の問に答えよ．

  1. 男女関係無く選ぶときの場合の数は何通りか．
  2. 男子から2人，女子から2人選ぶときの場合の数は何通りか．
  3. 男子から3人，女子から1人選ぶときの場合の数は何通りか．

  1. $_{10}\mathrm{C}_{4}=\dfrac{10\cdot 9\cdot 8\cdot 7}{4\cdot 3\cdot 2\cdot 1}=\boldsymbol{210}$ 通り
  2. 男子2人の組合せそれぞれに対して，女子2人の組合せが決められるので

    3. $_{5}\mathrm{C}_{2}\cdot\ _{5}\mathrm{C}_{2}=\dfrac{5\cdot 4}{2\cdot 1}\cdot \dfrac{5\cdot 4}{2\cdot 1}=\boldsymbol{100}$ 通り

  3. 男子3人の組合せそれぞれに対して，女子1人の組合せが決められるので

    4. $_{5}\mathrm{C}_{3}\cdot\ _{5}\mathrm{C}_{1}=\dfrac{5\cdot 4\cdot 3}{3\cdot 2\cdot 1}\cdot \dfrac{5}{1}=\boldsymbol{50}$ 通り

組合せ〜その2〜

説明文
説明文

  1. 図のように，横に4本，縦に7本の直行する平行線が引かれている． この中に長方形はいくつあるか求めよ．
  2. 正十角形の対角線の本数を求めよ．

  1. 横4本の平行線のうちから2本，縦7本の平行線のうちから2本をそれぞれ選べば，1個の長方形が定まる．

    2. よって

    $_{4}\mathrm{C}_{2}\cdot\ _{7}\mathrm{C}_{2}=\boldsymbol{126}$ 本

  2. 10個の頂点のうち2個を選べば，1本の対角線または辺が定まる．辺の数は10本であるから，これを除いて

    3. $_{10}\mathrm{C}_{2}-10=45-10=\boldsymbol{35}$ 本

組み分け

10人を次のように分ける方法は何通りあるか．

  1. 7人，3人に分ける．
  2. 5人，5人に分ける．
  3. 4人，3人，3人に分ける．
  4. 2人，2人，2人，2人，2人に分ける．

  1. 10人から3人を選びグループとし，残った7人をもうひとつのグループにすればよい．よって

    2. $_{10}\mathrm{C}_{3}\cdot\ _{7}\mathrm{C}_{7}=\dfrac{10\cdot 9\cdot 8}{3\cdot 2\cdot 1}\cdot1=\boldsymbol{120}$ 通り

  2. 10人から5人を選びグループとし，残った5人をもうひとつのグループにすればよい．

    3. しかし，10人を $a,b,c,d,e,f,g,h,i,j$ とすると，例えばはじめに $a,b,c,d,e$ の5人を 選んだ場合と，はじめに $f,g,h,i,j$ を選んだ場合では，どちらも

    \begin{align} (a,b,c,d,e)(f,g,h,i,j) \end{align}

    という2つのグループに分かれるという点では同じである．つまり，これらは2つで1通りと数えなければならない．

    他の選び方でも同様のことがいえるので，2で割ることにより重複の分を修正して

    \begin{align} \dfrac{_{10}\mathrm{C}_{5}\cdot\ _{5}\mathrm{C}_{5}}{2} &=\dfrac{10\cdot 9\cdot 8\cdot 7\cdot 6}{5\cdot 4\cdot 3\cdot 2\cdot 1}\cdot1\cdot\dfrac{1}{2}\\ &=\boldsymbol{126}通り \end{align}
  3. 最初に4人選びグループとし，残った6人から3,3人のグループをつくればよい． ただし，3人のグループが2つあるので，2. と同じように重複した分は修正する必要がある．
    4. \begin{align} &\ \frac{_{10}\mathrm{C}_{4}\cdot\ _{6}\mathrm{C}_{3}\cdot\ _{3}\mathrm{C}_{3}}{2}\\ =&\ \frac{10\cdot 9\cdot 8\cdot 7}{4\cdot 3\cdot 2\cdot 1}\cdot \frac{6\cdot 5\cdot 4}{3\cdot 2\cdot 1}\cdot \frac{1}{2}\\ =&\ \boldsymbol{2100} \end{align}

    ∴2100通り

  4. 2人ずつ選んでいって，重複を修正すると
    5. \begin{align} &\ \frac{_{10}\mathrm{C}_{2}\cdot\ _{8}\mathrm{C}_{2}\cdot\ _{6}\mathrm{C}_{2}\cdot\ _{4}\mathrm{C}_{2}\cdot\ _{2}\mathrm{C}_{2}}{5!}\\ =&\ \frac{10\cdot 9}{2\cdot 1}\cdot \frac{8\cdot 7}{2\cdot 1}\cdot \frac{6\cdot 5}{2\cdot 1}\\ &\qquad\cdot \frac{4\cdot 3}{2\cdot 1}\cdot \frac{1}{5\cdot 4\cdot 3\cdot 2\cdot 1}\\ =&\ \boldsymbol{945} \end{align}

    ∴945通り

ボールと箱のモデル4

説明文
説明文

$_{5}\mathrm{C}_{3}$ の定義は

「区別する5個のものから3個とりだして作る組の総数」

であったが，これはボールと箱のモデルを使って

「区別しない3個のボールを，区別する5個の箱に多くても1個配る場合の数」

といいかえることができる．これは，次のように説明できる．

準備として，3つのボールは区別しないでそれを $\bigcirc{}$ , $\bigcirc{}$ , $\bigcirc{}$ とし， 箱は区別するので番号をつけ，それをとしておく．

3つの区別しないボールを，5つの区別する箱に高々1個配る場合の総数は，結局5つの箱からボールを入れるための箱を3つ選ぶ 選び方と等しくなり，これは「区別する5個のものから3個とりだして作る組の総数」と考えることができるので $_{5}\mathrm{C}_{3}=\frac{5\cdot4\cdot3}{3\cdot2\cdot1}=10$ 通りとなる．

一般に，次のようにまとめることができる．

組合せ $_{n}\mathrm{C}_{r}$ のボールと箱のモデル

組合せ $_{n}\mathrm{C}_{r}$ はボールと箱のモデルを用いて

「区別しない $r$ 個のボールを，区別する $n$ 個の箱に高々1個配る場合の総数」

と考えることができる．

同じものを含む順列

同じものを含む順列$\text{C}(n_1,n_2,\cdots,n_m)$の定義

（注）
同じものを含む順列の定義
同じものを含む順列の定義

例えば，6枚のカード $\fbox{A},\fbox{A},\fbox{A},\fbox{B},\fbox{B},\fbox{C}$ を1列に 並べる順列の総数は次のように求めることができる．ただし，ここでは $\fbox{A}$ の3枚や， $\fbox{B}$ の2枚の並べ方の違いは区別しないものとする．

まず，カードを並べるための“部屋”を先に6つ用意しておく．

3枚の $\fbox{A}$ の入れる部屋の選び方は $_{6}\mathrm{C}_{3}$ 通りあり， その選んだ部屋に $\fbox{A}$ を入れる．

そのそれぞれに対し，残りの部屋は3部屋であるから，2枚の $\fbox{B}$ の入れる部屋の選び方は $_{3}\mathrm{C}_{2}$ 通りあり，その選んだ部屋に $\fbox{B}$ を入れる．

そのそれぞれに対し，残りの部屋は1つであるから，最後に $\fbox{C}$ を入れる．

以上から，6枚のカード $\fbox{A},\fbox{A},\fbox{A},\fbox{B},\fbox{B},\fbox{C}$ を1列に 並べる順列の総数は積の法則より

\begin{align} &_{6}\mathrm{C}_{3}\times\ _{3}\mathrm{C}_{2}\times\ _{1}\mathrm{C}_{1}\\ =&\frac{6\cdot5\cdot4}{3\cdot2\cdot1}\times\frac{3\cdot2}{2\cdot1}\times\frac{1}{1}=60 \end{align}

∴60通り

となる．

ここで，数個の区別しないものを含む $n$ 個の順列を定義しておこう．

同じものを含む順列 $\text{C}(n_1,n_2,\cdots,n_m)$ の定義

第 $i$ 種 $(1\leqq{i}\leqq{m})$ のものが $n_i$ 個ずつ全部で $n_1+n_2+\cdots+n_m=n$ 個あり，同種のものは区別しないものとするとき， これら $n$ 個を1列に並べた順列のことを，

同じものを含む順列

または，

一般順列(generalized permutation)

といい，その総数を $FTEXT$ では $\text{C}(n_1,~n_2,~\cdots,~n_m)$ と表す．

例えば， $a$ が3個， $b$ が2個， $c$ が1個の計6個の同じものを含む順列の総数は， $\text{C}(3,~2,~1)$ である．

この例より， $\text{C}(3,~2,~1)=60$ である．

同じものを含む順列$\text{C}(n_1,n_2,\cdots,n_m)$の計算

今みた例と同じように，一般の $\text{C}(n_1,~n_2,~\cdots,~n_m)$ も，以下のように考えることができる．

まず，カードを並べるための場所を先にn個用意しておく．

$n_1$ 個の同種のものの入れる場所の選び方は $_{n}\mathrm{C}_{n_1}$ 通りあり，またそのそれぞれに対して $n_2$ 個の同種のものの入れる場所の選び方は $_{n-n_1}\mathrm{C}_{n_2}$ 通りあり，またそのそれぞれに対して $n_3$ 個の同種のものの入れる場所の選び方は $_{n-n_1-n_2}\mathrm{C}_{n_3}$ 通りあり， $\cdots$ ，またそのそれぞれに対して $n_m$ 個の同種のものの入れる場所の選び方は $_{n-n_1-n_2-…-n_{m-1}}\mathrm{C}_{n_m}$ 通りある．

以上から，同じものを含む $n$ 個の順列は，積の法則から

\begin{align} &\ \text{C}(n_1,~n_2,~\cdots,~n_m)\\ =&\ _{n}\mathrm{C}_{n_1}\times\ _{n-n_1}\mathrm{C}_{n_2}\times\ _{n-n_1-n_2}\mathrm{C}_{n_3}\\ &\qquad\qquad\times\cdots\times\ _{n-n_1-n_2-\cdots-n_{m-1}}\mathrm{C}_{n_m} \end{align}

となる．

まとめると

同じものを含む順列 $\text{C}(n_1,n_2,…,n_m)$ の計算

第 $i$ 種 $(1\leqq{i}\leqq{m})$ のものが $n_i$ 個ずつ全部で $n_1+n_2+\cdots+n_m=n$ 個あり，同種のものは区別しないときの 同じものを含む順列の総数 $\text{C}(n_1,n_2,\cdots,n_m)$ は

\begin{align} &\ \text{C}(n_1,~n_2,~\cdots,~n_m)\\ =&\ _{n}\mathrm{C}_{n_1}\times\ _{n-n_1}\mathrm{C}_{n_2}\times\\ &\qquad\cdots\times\ _{n-n_1-\cdots{n}_{m-1}}\mathrm{C}_{n_m}\tag{1}\label{Cnokeisan1}\\ =&\ \frac{n!}{(n-n_1)!n_1!}\\ &\times\frac{(n-n_1)!}{(n-n_1-n_2)!n_2!}\times\\ &\cdots\times\frac{(n-n_1-\cdots-n_{m-1})!}{0!n_m!}\\ =&\ \frac{n!}{n_1!n_2!n_3!\cdots n_m!}\tag{2}\label{Cnokeisan2} \end{align}

と計算できる．

例えば， $a$ が3個， $b$ が2個， $c$ が1個の計6個の順列の総数は $\eqref{Cnokeisan1}$ を用いて

\begin{align} \text{C}(3,2,1)=&\ _{6}\mathrm{C}\ _{3}\times\ _{6-3}\mathrm{C}_{2}\times\ _{6-3-2}\mathrm{C}_{1}\\ =&\ _{6}\mathrm{C}_{3}\times\ _{3}\mathrm{C}_{2}\times\ _{1}\mathrm{C}_{1}=60 \end{align}

または， $\eqref{Cnokeisan2}$ を用いて

\begin{align} \text{C}(3,~2,~1) =&\frac{6!}{3!2!1!}=60 \end{align}

と計算できる．

上の $\eqref{Cnokeisan2}$ ， $\text{C}(n_1,~n_2,~\cdots,~n_m)=\dfrac{n!}{n_1!n_2!n_3!\cdots n_m!}$ は，ただ計算の上でいえるだけでなく

「 $n$ 個のものすべてを区別した $n!$ 通りの順列のうち，同種の $n_1,n_2,\cdots,n_m$ 個 の並び替えについては同一視するため， $n_1!n_2!\cdots n_m!$ 通りで一まとめにして数えたもの」

と考えることもできる．

同じものを含む順列

  1. $1,1,1,2,2,3,3$ の7つの数字を一列に並び替えるとき，何通りの並べ方があるか．
  2. SUUGAKUAを並び替えるとき，何通りの並べ方があるか．

  1. 1を3つ，2を2つ，3を2つ含むから
    2. \begin{align} \text{C}(3,~2,~2)=&\ _{7}\mathrm{C}_{3}\times\ _{7-3}\mathrm{C}_{2}\cdot\ _{7-3-2}\mathrm{C}_{2}\\ =&\ _{7}\mathrm{C}_{3}\times\ _{4}\mathrm{C}_{2}\times\ _{2}\mathrm{C}_{2}=\boldsymbol{210} \end{align}

    ∴210通り

    《別解》

    $\text{C}(3,~2,~2)=\dfrac{7!}{3! 2! 2!}=\boldsymbol{210}$ 通り

  2. Uを3つ，Aを2つ，S，G，Kをそれぞれ1つ含むから
    3. \begin{align} &\ \text{C}(3,~2,~1,~1,~1)\\ =&\ _{8}\mathrm{C}_{3}\cdot\ _{8-3}\mathrm{C}_{2}\cdot\ _{8-3-2}\mathrm{C}_{1}\\ &\qquad\cdot\ _{8-3-2-1}\mathrm{C}_{1}\cdot\ _{8-3-2-1-1}\mathrm{C}_{1}\\ =&\ _{8}\mathrm{C}_{3}\times\ _{5}\mathrm{C}_{2}\times\ _{3}\mathrm{C}_{1}\times\ _{2}\mathrm{C}_{1}\times\ _{1}\mathrm{C}_{1}\\ =&\ \boldsymbol{3360} \end{align}

    ∴3360通り

    《別解》

    \begin{align} \text{C}(3,~2,~1,~1,~1)=&\ \frac{8!}{3! 2! 1! 1! 1!}\\ =&\ \boldsymbol{3360}通り \end{align}

$_{n}\text{C}_{r}$の性質

$_{n}\text{C}_{r}$の性質

組合せ $_{n}\mathrm{C}_{r}$ について次の式が成り立つ．

$_{n}\mathrm{C}_{r}$ の性質

  1. $_{n}\mathrm{C}_{r}=\ _{n}\mathrm{C}_{n-r}$

    2. (選ばれるもの・選ばれないもの)

  2. $_{n}\mathrm{C}_{r}=\ _{n-1}\mathrm{C}_{r}+\ _{n-1}\mathrm{C}_{r-1}$

    3. (特定のものについての場合分け)

  3. $r_{n}\mathrm{C}_{r}=n\ _{n-1}\mathrm{C}_{r-1}$

    4. (リーダーの公式)

暗記$_{n}\mathrm{C}_{r}$ の性質の証明

上の i. ～ iii. が成り立つことを，

  1. 計算式を用いた方法
  2. 組合せの意味を考えた説明

でそれぞれ証明せよ．

  1. $_{n}\mathrm{C}_{r}=\ _{n}\mathrm{C}_{n−r}$
    1. ～計算式を用いた方法～
      2. \begin{align} &\ _{n}\mathrm{C}_{r}\\ =&\ \frac{_{n}\mathrm{P}_{r}}{r!}\\ =&\ \frac{n!}{(n-r)!r!}\\ =&\ \frac{1}{(n-r)!}\cdot\frac{n!}{r!}\\ =&\ \frac{1}{(n-r)!}\cdot\frac{n!}{\left\{n-(n-r)\right\}!}\\ =&\ \frac{1}{(n-r)!}\cdot\ _{n}\mathrm{P}_{n-r}\\ =&\ \frac{_{n}\mathrm{P}_{n-r}}{(n-r)!}\\ =&\ _{n}\mathrm{C}_{n-r} \end{align}

      $\uparrow$ 組合せ $_{n}\mathrm{C}_{r}$ の計算，順列 $_{n}\mathrm{P}_{r}$ の計算参照

    2. ～組合せの意味を考えた説明～

      3. 異なる $n$ 個の中から $r$ 個選ぶ $_{n}\mathrm{C}_{r}$ 通りそれぞれは， $n$ 個のものから選ばずに残す $(n−r)$ 個のものを選ぶ $_{n}\mathrm{C}_{n−r}$ 通りと 一対一に対応する．つまり， $r$ 個選ぶとは，選ばない $n−r$ を「選ぶ」ことと等しい． よって

      \begin{align} _{n}\mathrm{C}_{r}=\ _{n}\mathrm{C}_{n-r} \end{align}

      が成り立つ．

  2. $_{n}\mathrm{C}_{r}=\ _{n−1}\mathrm{C}_{r}+\ _{n−1}\mathrm{C}_{r−1}$
    1. ～計算式を用いた方法～
      2. \begin{align} &\ _{n-1}\mathrm{C}_{r}+\ _{n-1}\mathrm{C}_{r-1}\\ =&\frac{_{n-1}\mathrm{P}_{r}}{r!}+\frac{_{n-1}\mathrm{P}_{r-1}}{(r-1)!}\\ =&\frac{(n-1)!}{\left\{(n-1)-r\right\}!r!}\!\\ &\qquad+\!\frac{(n-1)!}{\left\{(n-1)-(r-1)\right\}!(r-1)!}\\ =&\frac{(n-1)!}{(n-r-1)!r!}+\frac{(n-1)!}{(n-r)!(r-1)!}\\ =&\frac{(n-1)!}{(n-r-1)!(r-1)!}\left\{\frac{1}{r}+\frac{1}{n-r}\right\}\\ =&\frac{(n-1)!}{(n-r-1)!(r-1)!}\cdot\frac{n}{r(n-r)}\\ =&\frac{n!}{(n-r)!r!}\\ =&\frac{_{n}\mathrm{P}_{r}}{r!}\\ =&_{n}\mathrm{C}_{r} \end{align}

      $\uparrow$ 組合せ $_{n}\mathrm{C}_{r}$ の計算，順列 $_{n}\mathrm{P}_{r}$ の計算参照

    2. ～組合せの意味を考えた説明～

      3. 異なるn個のものの中からr個選ぶ方法は，次の2つの場合に分けることができる．

      1. ある特定の1個を含まないで $r$ 個選ぶ

        2. $\uparrow\ _{n−1}\mathrm{C}_{r}$ 通り

      2. ある特定の1個を含んで $r$ 個選ぶ

        3. $\uparrow\ _{n−1}\mathrm{C}_{r−1}$ 通り

      この2つは同時に起こることはないので

      \begin{align} _{n}\mathrm{C}_{r}=\ _{n-1}\mathrm{C}_{r}+\ _{n-1}\mathrm{C}_{r-1} \end{align}

      $\uparrow$ 和の法則

      が成り立つ．

  3. $r\ _{n}\mathrm{C}_{r}=n\ _{n-1}\mathrm{C}_{r-1}$
    1. ～計算式を用いた方法～
      2. \begin{align} &\ r\ _{n}\mathrm{C}_{r}\\ =&\ r\times\frac{_{n}\mathrm{P}_{r}}{r!}\\ =&\ r\times\frac{n!}{(n-r)!r!}\\ =&\ \frac{n!}{(n-r)!(r-1)!}\\ =&\ n\times\frac{(n-1)!}{\left\{n-1-(r-1)\right\}!(r-1)!}\\ =&\ n\times\frac{_{n-1}\mathrm{P}_{r-1}}{(r-1)!}\\ =&\ n\ _{n-1}\mathrm{C}_{r-1} \end{align}

      $\uparrow$ 組合せ $_{n}\mathrm{C}_{r}$ の計算，順列 $_{n}\mathrm{P}_{r}$ の計算参照

    2. ～組合せの意味を考えた説明～

      3. $n$ 人の中から $r$ 人の班をつくり班長を決める場合の数について考える． $n$ 人の中から班員 $r$ 人選び，その $r$ 人の中からリーダーを1人決める方法には $_{n}\mathrm{C}_{r}\times{r}$ 通りある． また別の方法として， $n$ 人の中から先にリーダーを決めておき，残りの班員 $r−1$ 人を選ぶ方法には $n\ _{n−1}\mathrm{C}_{r−1}$ 通りある． よって

      \begin{align} r_{n}\mathrm{C}_{r}=n\ _{n-1}\mathrm{C}_{r-1} \end{align}

      が成り立つ．

最短経路

説明文
説明文

図のように，東西に走る道路と南北に走る道路があるとする．南西の角にあるA地点から，北東の角にあるB地点に至る

最短経路について以下の問に答えよ．

  1. 最短経路は全部で何通りあるか求めよ．
  2. C地点を通る最短経路は何通りあるか．また，D地点を通る最短経路は何通りあるか，それぞれ求めよ．
  3. C地点またはD地点を通る最短経路は何通りあるか求めよ．

北に1区画進むことを↑，東に1区画進むことを→で表すと，例えば図のように進む場合には

$\uparrow\rightarrow\rightarrow\rightarrow\uparrow\uparrow\rightarrow\uparrow\uparrow\rightarrow\rightarrow$

と表すことができる．

  1. 北に1区画進むことを $\uparrow$ ，東に1区画進むことを $\rightarrow$ で表すと，A地点からB地点への最短経路は，5個の $\uparrow$ と6個の $\rightarrow$ ($\uparrow\uparrow\uparrow\uparrow\uparrow\rightarrow\rightarrow\rightarrow\rightarrow\rightarrow\rightarrow$ ) を一列に並べる順列の総数に等しい．

    2. よって，求める最短経路の数は

    $\dfrac{11!}{5!6!}=\boldsymbol{462}$ 通り

    $\uparrow$ 同じ物を含む順列 $\text{C}(n_1,n_2,\cdots,n_m)$ の計算

    となる．

    1. (C地点を通る最短経路)

      2. まず，A地点からC地点までの最短経路の数は

      $\dfrac{4!}{2!2!}=6$ 通り

      であり，この6通りそれぞれに対し，C地点からB地点までの最短経路

      $\dfrac{7!}{3!4!}=35$ 通り

      が決まるから，積の法則より

      $6\times35=\boldsymbol{210}$ 通り

    2. (D地点を通る最短経路)

      3. 同様にして

      $\dfrac{7!}{4!3!}\times\dfrac{4!}{1!3!}=35\times4=\boldsymbol{140}$ 通り

  3. 集合C,Dをそれぞれ

    4. $C$ :C地点を通る最短経路

    $D$ :D地点を通る最短経路

    とおくと， $n(C\cap D)$ ，つまりC，D両地点を通る最短経路の数は

    \begin{align} n(C\cap D)=&\ \frac{4!}{2!2!}\times\frac{3!}{2!1!}\times\frac{4!}{1!3!}\\ =&\ 6\times3\times4=72 \end{align}

    であるから， $n(C\cup D)$ ，つまり求める最短経路の数は

    \begin{align} n(C\cup D)&=n(C)+n(D)-n(C\cap D)\\ &=210+140-72=\boldsymbol{278} \end{align}

    ∴278通り

    $\uparrow$ 包含と排除の原理 (2集合版)

2項定理

$(a+b)^n$を展開するということ

$(a+b)^2$ を展開すると

\begin{align} (a+b)^2=a^2+2ab+b^2 \end{align}

また， $(a+b)^3$ を展開すると

\begin{align} (a+b)^3=a^3+3a^2b+3ab^2+b^3 \end{align}

である．

ここでは，自然数 $n$ について， $(a+b)^n$ を展開した式を組合せを使って求める方法について考えてみよう． 以下では例として， $(a+b)^5$ の展開についてみていこう．

$(a+b)^5$ とは，5つの $(a+b)$ の積

のことである．この展開式は，5つの $(a+b)$ のそれぞれから， $a$ か $b$ のどちらかをとって，掛け合わせたものの和になる．

$a^4b$の係数はいくつになるのか

5つの $(a+b)$ のうち，1つから $b$ を選び，残りの4つから $a$ をとって掛け合わせると， $a^4b$ が作られる．

図は，①から $b$ をとった場合のイメージである．

ここで， $a^4b$ が作られる場合の数は，上の①から⑤の1ヶ所から $b$ を選べばよいので，組合せの考えを使って $_{5}\mathrm{C}_{1}$ と数えることができる．

つまり， $(a+b)^5$ の展開式における $a^4b$ の係数は $_{5}\mathrm{C}_{1}=5$ である．

$a^3b^2$の係数はいくつになるのか

5つの $(a+b)$ のうち，2つから $b$ を選び，残りの3つから $a$ をとって掛け合わせると， $a^3b^2$ が作られる．

図は，②と⑤から $b$ をとった場合のイメージである．

ここで， $a^3b^2$ が作られる場合の数は，上の①から⑤の2ヶ所から $b$ を選べばよいので，組合せの考えを使って $_{5}\mathrm{C}_{2}$ と数えることができる．

つまり， $(a+b)^5$ の展開式における $a^3b^2$ の係数は $_{5}\mathrm{C}_{2}=\dfrac{5\cdot4}{2\cdot1}=10$ である．

$(a+b)^5$の展開式

以上の例から， $(a+b)^5$ の展開式における各項の係数は，それぞれ次のようになるのがわかる．

$a^5$ の係数は5つの $(a+b)$ のうち0ヶ所から $b$ を選ぶと考えて $_{5}\mathrm{C}_{0}$

$a^4b$ の係数は5つの $(a+b)$ のうち1ヶ所から $b$ を選ぶと考えて $_{5}\mathrm{C}_{1}$

$a^3b^2$ の係数は5つの $(a+b)$ のうち2ヶ所から $b$ を選ぶと考えて $_{5}\mathrm{C}_{2}$

$a^2b^3$ の係数は5つの $(a+b)$ のうち3ヶ所から $b$ を選ぶと考えて $_{5}\mathrm{C}_{3}$

$ab^4$ の係数は5つの $(a+b)$ のうち4ヶ所から $b$ を選ぶと考えて $_{5}\mathrm{C}_{4}$

$b^5$ の係数は5つの $(a+b)$ のうち5ヶ所から $b$ を選ぶと考えて $_{5}\mathrm{C}_{5}$

つまり

\begin{align} (a+b)^5&=\ _{5}\mathrm{C}_{0}a^5+\ _{5}\mathrm{C}_{1}a^4b+\ _{5}\mathrm{C}_{2}a^3b^2\\ &\qquad+\ _{5}\mathrm{C}_{3}a^2b^3+\ _{5}\mathrm{C}_{4}ab^4+\ _{5}\mathrm{C}_{5}b^5 \end{align}

となる．

$(a+b)^n$の展開式(2項定理)

一般に， $(a+b)^n$ の展開式における $a^{n−r}b^r$ の係数は， $n$ 個の $(a+b)$ のうち， $r$ 個から $b$ を，残りの $n−r$ 個から $a$ を取り出す方法の総数 $_{n}\mathrm{C}_{r}$ となる．このことから，次の式(2項定理(binomial theorem))が成り立つことがわかる．

2項定理

$n$ を自然数とするとき， $(a+b)^n$ は

\begin{align} (a+b)^n&=\ _{n}\mathrm{C}_{0}a^n+\ _{n}\mathrm{C}_{1}a^{n-1}b+\cdots\\ &\qquad+\ _{n}\mathrm{C}_{n-1}ab^{n-1}+\ _{n}\mathrm{C}_{n}b^n \end{align}

と展開できる．

2項定理の係数になるという意味で，組合せの総数 $_{n}\mathrm{C}_{r}$ のことを2項係数(binomial coefficient)ともいう．

例えば， $(a+2b)^4$ は2項定理を用いて

\begin{align} &(a+2b)^4\\ =&\ _{4}\mathrm{C}_{0}a^4+\ _{4}\mathrm{C}_{1}a^3(2b)+\ _{4}\mathrm{C}_{2}a^2(2b)^2\\ &\qquad+\ _{4}\mathrm{C}_{3}a(2b)^3+\ _{4}\mathrm{C}_{4}(2b)^4\\ =&\ a^4+4a^3(2b)+6a^2(2b)^2+4a(2b)^3+(2b)^4\\ =&\ a^4+8a^3b+24a^2b^2+32ab^3+16b^4 \end{align}

と展開できる．

展開された式の係数

次の展開式において， $\left[\quad\right]$ 内で指定された項の係数を求めよ．

  1. $(2x+1)^6\qquad[x^2]$
  2. $(2x-3y)^5\qquad[x^3y^2]$
  3. $\left(x^2-\dfrac{1}{2x}\right)^7\qquad\left[\frac{1}{x}\right]$
  4. $\left(x-\dfrac{1}{2x^2}\right)^{12}\qquad[定数項]$

  1. $(2x+1)^6$ を展開したとき， $x^2$ を含む項は
    2. \begin{align} _{6}\mathrm{C}_{4}(2x)^21^4 \end{align}

    $\uparrow$ 2項定理を部分的に使った

    となる．よって， $x^2$ の係数は

    \begin{align} _{6}\mathrm{C}_{4}\cdot2^2=\boldsymbol{60} \end{align}
  2. $(2x−3y)^5$ を展開したとき， $x^3y^2$ を含む項は
    3. \begin{align} _{5}\mathrm{C}_{2}(2x)^3(-3y)^2 \end{align}

    $\uparrow$ 2項定理を部分的に使った

    となる．よって， $x^3y^2$ の係数は \begin{align} _{5}\mathrm{C}_{2}\cdot2^3\cdot(-3)^2=\boldsymbol{720} \end{align}

  3. $(a+b)^7$ の展開において， $a=x^2,b=-\dfrac{1}{2x}$ としたものが $\left(x^2-\dfrac{1}{2x}\right)^7$ である． $a^2b^5$ を計算すると $\dfrac{1}{x}$ の項ができるので，このときの係数を求める．
    4. \begin{align} &_{7}\mathrm{C}_{5}a^2b^5\\ =\ &_{7}\mathrm{C}_{5}(x^2)^2\left(-\frac{1}{2x}\right)^5\\ =\ &_{7}\mathrm{C}_{5}\left(-\frac{1}{2}\right)^5\frac{1}{x}\\ =\ &-\frac{21}{32}\cdot\frac{1}{x} \end{align}

    $\uparrow$ 2項定理を部分的に使った

    よって，求める係数は $\boldsymbol{-\dfrac{21}{32}}$である．

  4. $(a+b)^{12}$ の展開において， $a=x,b=-\dfrac{1}{2x^2}$ としたものが $\left(x-\dfrac{1}{2x^2}\right)^{12}$ である． $a^8b^4$ を計算すると定数項ができるので，このときの係数を求める．

    \begin{align} &_{12}\mathrm{C}_{4}a^8b^4\\ =\ &_{12}\mathrm{C}_{4}x^8\left(-\frac{1}{2x^2}\right)^4\\ =\ &_{12}\mathrm{C}_{4}\left(-\frac{1}{2}\right)^4\\ =\ &\frac{495}{16} \end{align}

    $\uparrow$ 2項定理を部分的に使った

    よって，求める係数は $\boldsymbol{\dfrac{495}{16}}$ である．

2項定理の応用

次の展開式において， $[\quad]$ 内で指定された項の係数を求めよ．

  1. $(2x+y-z)^8\qquad[x^2y^3z^3]$
  2. $(x-2y-z)^5\qquad[x^2yz^2]$

  1. $(2x+y-z)^8=\left\{2x+(y-z)\right\}^8$ として考える．

    2. これを展開したとき， $x^2$ の項は

    \begin{align} _{8}\mathrm{C}_{6}(2x)^2(y-z)^6 \end{align}

    $\uparrow$ 2項定理を部分的に使った

    として計算される．

    さらに $(y−z)^6$ を展開したとき， $y^3$ の項は

    \begin{align} _{6}\mathrm{C}_{3}y^3(-x)^3 \end{align}

    $\uparrow$ 2項定理を部分的に使った

    として計算される．

    よって， $(2x+y-z)^8$ を展開したときの $x^2y^3z^3$ の係数は

    \begin{align} &_{8}\mathrm{C}_{6}\cdot\ 2^2\cdot\ _{6}\mathrm{C}_{3}\cdot(-1)^3\\ =\ &-4\cdot\ _{8}\mathrm{C}_{2}\cdot\ _{6}\mathrm{C}_{3}=\boldsymbol{-2240} \end{align}
  2. $(x-2y-z)^5=\left\{x+(-2y-z)\right\}^5$ として考える． これを展開したとき， $x^2$ の項は
    3. \begin{align} _{5}\mathrm{C}_{3}x^2(-2y-z)^3 \end{align}

    $\uparrow$ 2項定理を部分的に使った

    として計算される．

    さらに $(−2y−z)^3$ を展開したとき， $y$ の項は

    \begin{align} _{3}\mathrm{C}_{2}(-2y)(-z)^2 \end{align}

    $\uparrow$ 2項定理を部分的に使った

    として計算される．

    よって， $(x−2y−z)^8$ を展開したときの $x^2yz^2$ の係数は

    \begin{align} \ &_{5}\mathrm{C}_{3}\cdot\ _{3}\mathrm{C}_{2}\cdot(-2)\cdot(-1)^2\\ =\ &-2\cdot\ _{5}\mathrm{C}_{2}\cdot\ _{3}\mathrm{C}_{1}=\boldsymbol{-60} \end{align}

2項係数の和

2項定理を用いて次の等式を証明せよ．

  1. \begin{align} 2^n=&\ _{n}\mathrm{C}_{0}+\ _{n}\mathrm{C}_{1}+\ _{n}\mathrm{C}_{2}+\cdots\\ &\qquad+\ _{n}\mathrm{C}_{n-1}+\ _{n}\mathrm{C}_{n} \end{align}
  2. \begin{align} 0=&\ _{n}\mathrm{C}_{0}-\ _{n}\mathrm{C}_{1}+\ _{n}\mathrm{C}_{2}-\cdots\\ &\qquad+(-1)^{n-1}\ _{n}\mathrm{C}_{n-1}+(-1)^n\ _{n}\mathrm{C}_{n} \end{align}
  3. \begin{align} (-1)^n=&\ _{n}\mathrm{C}_{0}-2\ _{n}\mathrm{C}_{1}+2^2\ _{n}\mathrm{C}_{2}-\cdots\\ &+(-2)^{n-1}\ _{n}\mathrm{C}_{n-1}+(-2)^n\ _{n}\mathrm{C}_{n} \end{align}

2項定理

\begin{align} &\ (a+b)^n\\ =&\ _{n}\mathrm{C}_{0}a^n+\ _{n}\mathrm{C}_{1}a^{n-1}b+\ _{n}\mathrm{C}_{2}a^{n-2}b^2+\cdots\\ &\qquad+\ _{n}\mathrm{C}_{n-1}ab^{n-1}+\ _{n}\mathrm{C}_{n}b^n \end{align}

において

  1. $a=b=1$ とおくと
    2. \begin{align} 2^n=&\ _{n}\mathrm{C}_{0}+\ _{n}\mathrm{C}_{1}+\ _{n}\mathrm{C}_{2}+\cdots\\ &\qquad+\ _{n}\mathrm{C}_{n-1}+\ _{n}\mathrm{C}_{n} \end{align}

    となり，確かに成立する．

  2. $a=1,b=−1$ とおくと
    3. \begin{align} 0=&\ _{n}\mathrm{C}_{0}-\ _{n}\mathrm{C}_{1}+\ _{n}\mathrm{C}_{2}-\cdots\\ &+(-1)^{n-1}\ _{n}\mathrm{C}_{n-1}+(-1)^n\ _{n}\mathrm{C}_{n} \end{align}

    となり，確かに成立する．

  3. $a=1,b=−2$ とおくと
    4. \begin{align} &\ (-1)^n\\ =&\ _{n}\mathrm{C}_{0}-2\ _{n}\mathrm{C}_{1}+2^2\ _{n}\mathrm{C}_{2}-\cdots\\ &\qquad+(-2)^{n-1}\ _{n}\mathrm{C}_{n-1}+(-2)^n\ _{n}\mathrm{C}_{n} \end{align}

    となり，確かに成立する．

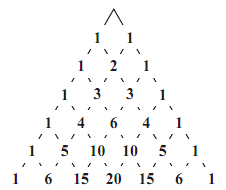
パスカルの三角形

図のように，2項係数 $_{n}\mathrm{C}_{0},\ _{n}\mathrm{C}_{1},\ _{n}\mathrm{C}_{2},\cdots,\ _{n}\mathrm{C}_{n}$ の値を，上から順に $n=1,2,3,\cdots$ の場合について三角形の形に並べたものを，パスカルの三角形(Pascal's triangle)という．

パスカルの三角形には，次のような特徴がある．

  1. $_{n}\mathrm{C}_{0}=\ _{n}\mathrm{C}_{n}=1$ であるから，各行の左右両端の数字は1である．
  2. $_{n}\mathrm{C}_{r}=\ _{n}\mathrm{C}_{n−r}$ であるから，各行は左右対称である．
  3. $_{n}\mathrm{C}_{r}=\ _{n−1}\mathrm{C}_{r-1}+\ _{n−1}\mathrm{C}_{r}$ であるから $_{n}\mathrm{C}_{r}$ の性質，左右両端以外の数字は，その左上の数と右上の数を足したものとなる．

パスカルの三角形

パスカルの三角形を利用して，次の展開式を求めよ．

  1. $(x+y)^6$
  2. $(x−2y)^5$

  1. パスカルの三角形を $n=6$ の場合まで書くと，図のようになるので
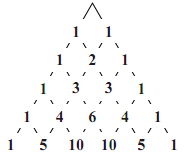
    2. \begin{align} &\ (x+y)^6\\ =&\ \boldsymbol{x^6+6x^5y+15x^4y^2+20x^3y^3}\\ &\ \qquad\qquad\boldsymbol{+15x^2y^4+6xy^5+y^6} \end{align}
  2. パスカルの三角形を $n=5$ の場合まで書くと，図のようになるので
    3. \begin{align} &\ (x-2y)^5\\ =&\ x^5+5x^4(-2y)+10x^3(-2y)^2\\ &\ +10x^2(-2y)^3+5x(-2y)^4+(-2y)^5\\ =&\ \boldsymbol{x^5-10x^4y+40x^3y^2}\\ &\ \boldsymbol{-80x^2y^3+80xy^4-32y^5} \end{align}