3倍角の公式
3倍角の公式
暗記3倍角の公式の導出
$\sin3\alpha$を$\sin\alpha$だけの式で表せ.また,$\cos3\alpha$を$\cos\alpha$だけの式で表せ.
\[\sin3\alpha=\sin(2\alpha +\alpha)\] \[=\sin2\alpha \cos\alpha +\cos2\alpha \sin\alpha\] ←正弦と余弦の加法定理 \[=(2\sin\alpha \cos\alpha)\cos\alpha +(1-2\sin^2\alpha)\sin\alpha\] ←2倍角の公式 \[=2\sin\alpha \cos^2\alpha +\sin\alpha -2\sin^3\alpha\] \[=2\sin\alpha(1-\sin^2\alpha) +\sin\alpha -2\sin^3\alpha\] ←拡張された三角関数の相互関係 \[=\boldsymbol{3\sin\alpha -4\sin^3\alpha}\] \[\cos3\alpha=\cos(2\alpha +\alpha)\] \[=\cos2\alpha \cos\alpha -\sin2\alpha \sin\alpha\] ←正弦と余弦の加法定理 \[=(2\cos^2\alpha -1)\cos\alpha +(2\sin\alpha\cos\alpha)\sin\alpha\] ←2倍角の公式 \[=2\cos^3\alpha -\cos\alpha +2\sin^2\alpha\cos\alpha\] \[=2\cos^3\alpha -\cos\alpha +2(1-\cos^2\alpha)\cos\alpha\] ←拡張された三角関数の相互関係 \[=\boldsymbol{4\cos^3\alpha -3\cos\alpha}\]
3倍角の公式
- $\sin3\alpha=3\sin\alpha -4\sin^3\alpha$
- $\cos3\alpha=4\cos^3\alpha -3\cos\alpha$
3倍角の公式の利用
$0\leqq x \leqq\pi$のとき,不等式$\cos3{x} +2\cos{x}=0$を満たす$x$を求めよ.
無題
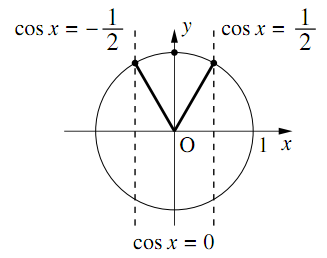
$\cos3{x} =4\cos^3{x} -3\cos{x}$なので
\begin{align} &\cos3{x} +2\cos{x} =0\\ \Leftrightarrow ~&4\cos^3{x} -3\cos{x} +2\cos{x}=0\\ \Leftrightarrow ~&(4\cos^2{x} -1)\cos{x} =0\\ \Leftrightarrow ~&\cos{x} =-\dfrac{1}{2},~ \dfrac{1}{2},~ 0 \end{align}$0\leqq {x} \leqq \pi$の範囲でこれを解いて,
$\boldsymbol{{x} =\dfrac{\pi}{3},~\dfrac{\pi}{2},~\dfrac{2}{3}\pi}$