平面図形
角の2等分線
内分と外分
内分と外分
内分
説明文
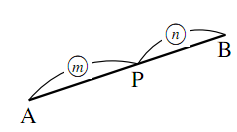
正の数 $m,n$ とする.線分 $\text{AB}$ 上の点 $\text{P}$ について
\[AP:PB=m:n\]が成り立つとき,点 $\text{P}$ は線分 $\text{AB}$ を $m:n$ に
内分(interior devision)
するといい, 点 $\text{P}$ のことを内分点という.
外分
正の数 $m,n$ とする.線分ABの延長上の点 $\text{Q}$ について
\[AQ:QB=m : n\]が成り立つとき,点 $\text{Q}$ は線分 $\text{AB}$ を $m:n$ に
外分(exterior devision)
するといい,点 $\text{Q}$ のことを外分点という.
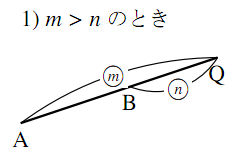
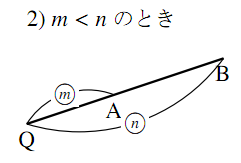
下図のように,点 $\text{Q}$ は
- $m\gt n$ のときは,線分 $\text{AB}$ の $\text{B}$ の方向への延長上
- $m\lt n$ のときは,線分 $\text{AB}$ の $\text{A}$ の方向への延長上
にある.
説明文
説明文
内分と外分
次の線分 $\text{AB}$ において,次の点を図示せよ.
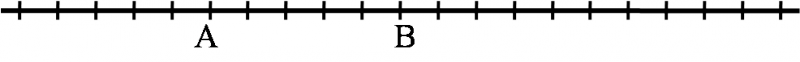
- $\text{AB}$ を $1:4$ に内分する点 $\text{P}$
- $\text{AB}$ を $3:2$ に外分する点 $\text{Q}$
- $\text{AB}$ を $3:2$ に内分する点 $\text{R}$
- $\text{AB}$ を $1:2$ に外分する点 $\text{S}$
角の2等分線の定理(幾何)
角の2等分線の定理
角の2等分線の定理
説明文
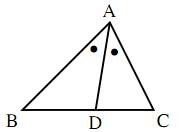
$\triangle{\mathrm{ABC}}$ において, $\angle{\mathrm{A}}$ の2等分線と辺 $\text{BC}$ との交点を $\text{D}$ とするとき
\[\text{AB}:\text{AC}=\text{BD}:\text{DC}\]が成り立つ.
証明
角の2等分線の定理
説明文

次の図の $\triangle{\mathrm{ABC}}$ において,点 $\text{D}$ は $\angle{\text{A}}$ の二等分線と辺 $\text{BC}$ との交点である.このとき,線分 $\text{BD}$ の長さを求めよ.
$BD=x$ とおくと,角の二等分線の定理より,
\begin{align} AB:AC&=BD:DC\\ 5:4&=x:(18-x)\\ 4x&=5(18-x)\\ 9x&=90\\ x&=10\\ \therefore\ \boldsymbol{BD}&=\boldsymbol{10} \end{align}三角形の外角の二等分線と比
説明文

$\triangle{\mathrm{ABC}}$ において, $\angle{\mathrm{A}}$ の外角の二等分線と辺 $\text{BC}$ の延長線との交点を $\text{D}$ とするとき
\[\text{AB}:\text{AC}=\text{BD}:\text{DC}\]が成り立つ.
三角形の外角の二等分線と比
説明文

次の図の $\triangle{\mathrm{ABC}}$ において,点Dは $\angle{\mathrm{A}}$ の外角の二等分線と半直線 $\text{BC}$ との交点である.このとき,線分 $\text{CD}$ の長さを求めよ.
$CD=x$ とおくと,外角の二等分線の定理より,
\begin{align} AB:AC&=BD:DC\\ 7:5&=(6+x):x\\ 7x&=5(6+x)\\ 2x&=30\\ x&=15\\ \therefore\ \boldsymbol{CD}&=\boldsymbol{15} \end{align}重心
重心とは何か
重心とは何か
中線について
重心
三角形の中線の交点を重心という.
重心の定理
重心の定理
重心
説明文
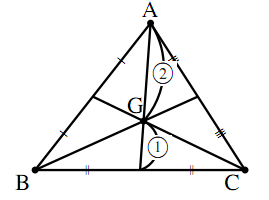
どんな三角形でも,各頂点から引いた3本の中線は1点で交わる.
つまり,どんな三角形でも重心は1つである。
図に示したように,重心は三角形の中線を $2:1$ に内分する.
証明
重心
説明文
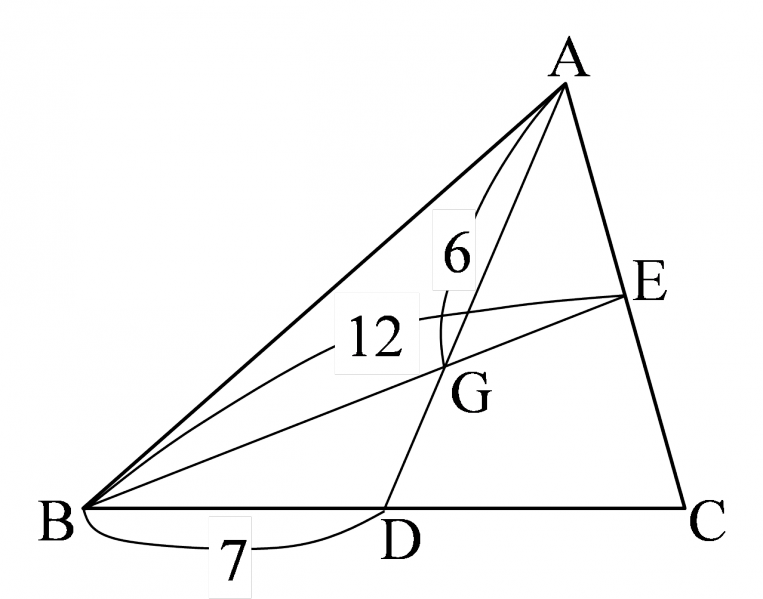
図において,次の線分の長さを求めよ.
ただし,点Gは $\triangle{\mathrm{ABC}}$ の重心とする.
- $\text{CD}$
- $\text{DG}$
- $\text{BG}$
- $\text{EG}$
- $CD=BD=\boldsymbol{7}$
- $DG=\dfrac{1}{2}AG=\dfrac{1}{2}\times6=\boldsymbol{3}$
- $BG=\dfrac{2}{3}BE=\dfrac{2}{3}\times12=\boldsymbol{8}$
- $EG=\dfrac{1}{3}EB=\dfrac{1}{3}\times12=\boldsymbol{4}$
内心
内心とは何か
内心とは何か
内心
三角形の内角の二等分線の交点を内心という.
内心の定理
内心の定理
内心
どんな三角形でも,3つの角の二等分線は1点で交わる.
証明
無題
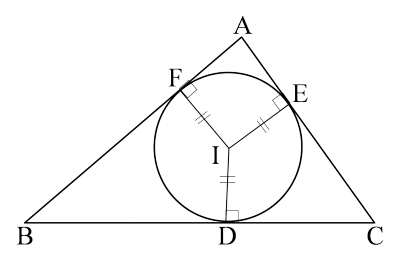
上の証明により,次のことがいえる.
\[\mathrm{ID}\perp\mathrm{BC},\mathrm{IE}\perp\mathrm{CA},\mathrm{IF}\perp\mathrm{AB}\] \[\mathrm{ID}=\mathrm{IE}=\mathrm{IF}\]よって,この点 $\mathrm{I}$ を中心とする半径 $\mathrm{ID}$ の円は, $\triangle{\mathrm{ABC}}$ の3辺に接する.
この円を $\triangle{\mathrm{ABC}}$ の内接円といい,点 $\mathrm{I}$ を $\triangle{\mathrm{ABC}}$ の内心という.
内心
無題
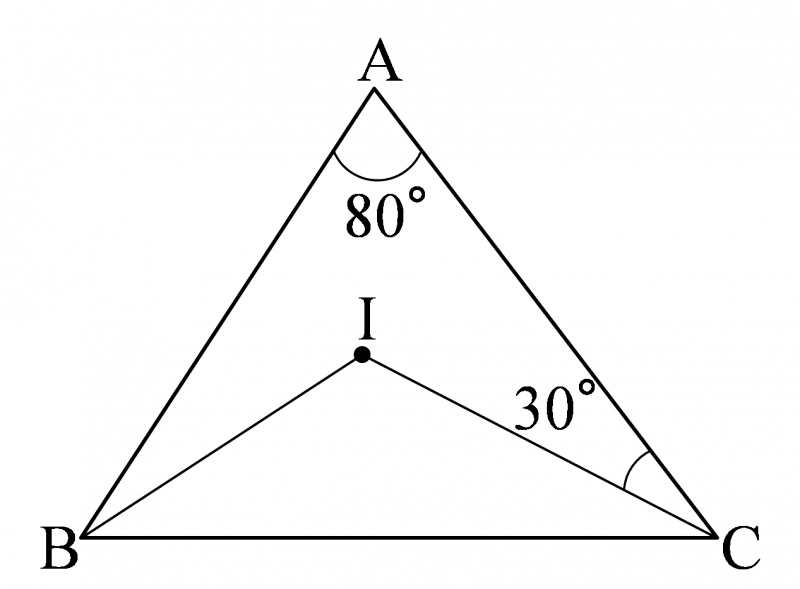
次の図において,次の角の大きさを求めよ.ただし,点 $\text{I}$ は $\triangle{\text{ABC}}$ の内心とする.
- $\angle{\text{ABI}}$
- $\angle{\text{BIC}}$
- $\triangle{\mathrm{ABC}}$ において,
- $\triangle{\mathrm{IBC}}$ において,
$2\angle{\text{ABI}}+30^\circ\times2+80^\circ=180^\circ$ より,
$\angle{\text{ABI}}=\boldsymbol{20^\circ}$
$20^\circ+30^\circ+\angle{\text{BIC}}=180^\circ$ より,
$\angle{\text{BIC}}=\boldsymbol{130^\circ}$
内接円の半径と三角形の面積
無題

次の図のような $\triangle{\mathrm{ABC}}$ があり,面積は $12\sqrt{15}$ である.この三角形の内接円の半径を求めよ.
無題

$\triangle{\mathrm{OAB}}+\triangle{\mathrm{OBC}}+\triangle{\mathrm{OCA}}=\triangle{\mathrm{ABC}}$ であることに着目する.
内接円の半径を $r$ とすると,
\begin{align} &\frac{1}{2}\times12\times{r}+\frac{1}{2}\times16\times{r}\\ &\qquad+\frac{1}{2}\times8\times{r}=12\sqrt{15} \end{align} \[r=\boldsymbol{\frac{2\sqrt{15}}{3}}\]外心
外心とは何か
外心とは何か
外心
三角形の3辺の垂直二等分線の交点を外心という.
外心の定理
外心の定理
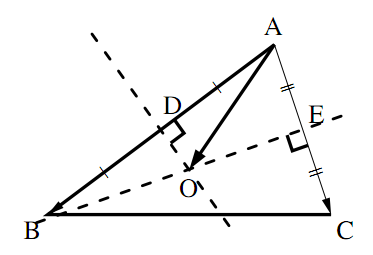
外心
どんな三角形でも,3辺の垂直二等分線は1点で交わる.
証明
無題
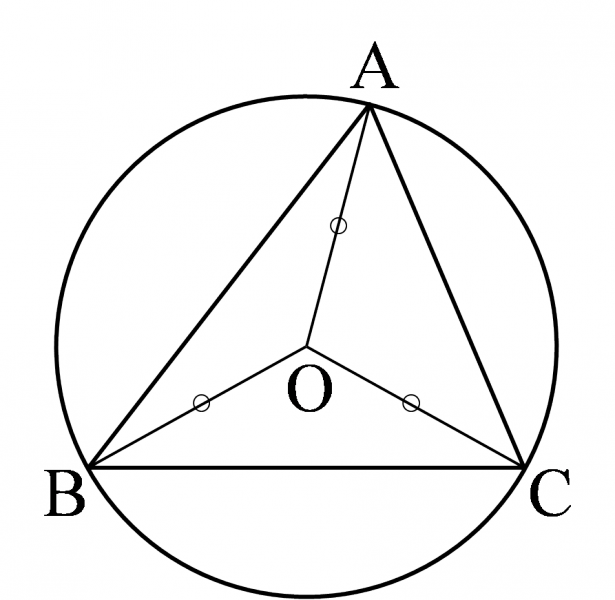
$\triangle{\mathrm{ABC}}$ において,3辺の垂直二等分線が交わる点を $\mathrm{O}$ とすると,上の証明により,点 $\mathrm{O}$ は $\triangle{\mathrm{ABC}}$ の3つの頂点から等距離にある.よって,この点 $\mathrm{O}$ を中心とする半径 $\mathrm{OA}$ の円は, $\triangle{\mathrm{ABC}}$ の3つの頂点を通る.
この円を, $\triangle{\mathrm{ABC}}$ の外接円といい,点 $\mathrm{O}$ を $\triangle{\mathrm{ABC}}$ の外心という.
外心
無題

次の図において,次の角の大きさを求めよ.ただし,点 $\text{O}$ は$\triangle{\mathrm{ABC}}$ の外心とする.
- $\angle{\text{ABO}}$
- $\angle{\text{BOC}}$
$\triangle{\mathrm{OAB}},\triangle{\mathrm{OBC}},\triangle{\mathrm{OCA}}$ は二等辺三角形である.
- $\angle{\mathrm{OAC}}=\angle{\mathrm{OCA}}=20^\circ$ より,
- $\triangle{\mathrm{ABC}}$ において,
$\angle{\mathrm{ABO}}=\angle{\mathrm{BAO}}=80^\circ-20^\circ=\boldsymbol{60^\circ}$
\begin{align} &20^\circ+80^\circ+60^\circ+\angle{\text{OBC}}+\angle{\text{OCB}}\\ &=180^\circ \end{align} よって,
$\angle{\text{OBC}}+\angle{\text{OCB}}=20^\circ$ だから, $\triangle{\mathrm{OBC}}$ において,
$\angle{\text{BOC}}=180^\circ-20^\circ=\boldsymbol{160^\circ}$
垂心
垂心とは何か
垂心とは何か
垂心
三角形の3つの頂点からの垂線の交点を垂心という.
垂心の定理
垂心の定理
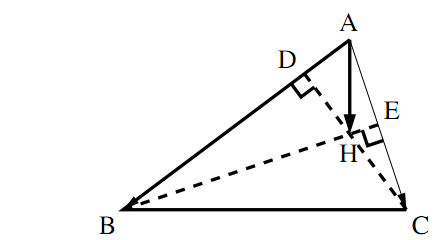
垂心
どんな三角形でも,3つの垂線は1点で交わる.
証明
垂心
空白
空白
オイラー線
オイラー線
オイラー線
三角形の重心・垂心・外心を通る直線をオイラー線という.
チェバの定理
チェバの定理
チェバの定理
チェバの定理
無題
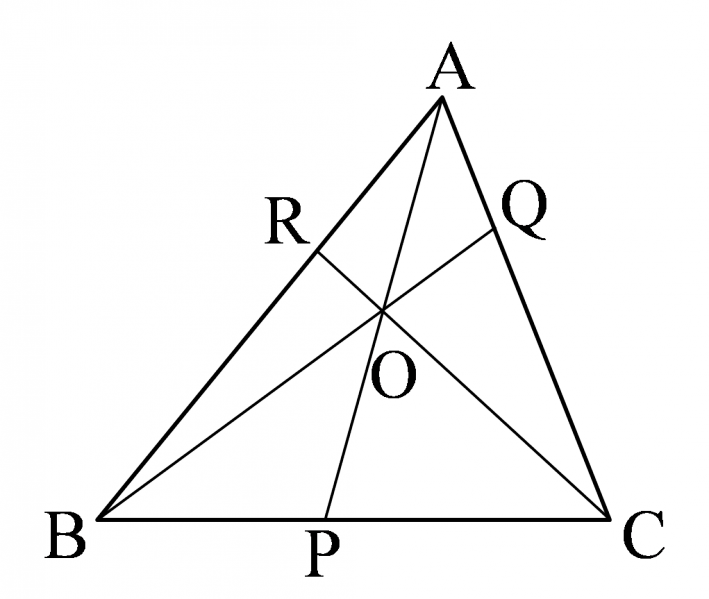
$\triangle{\mathrm{ABC}}$ の内部に点 $\mathrm{O}$ がある。頂点 $\mathrm{A},\mathrm{B},\mathrm{C}$ と $\mathrm{O}$ を結ぶ直線が向かい合う辺と,それぞれ $\mathrm{P},\mathrm{Q},\mathrm{R}$ で交わるとき
\[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}}=1\]証明
チェバの定理
無題

$\angle{\text{A}}=90^\circ,\text{AB}=3,\text{AC}=4$ の $\triangle{\mathrm{ABC}}$ がある.点 $\text{A}$ から辺 $\text{BC}$ に垂線を引き交点を $\text{P}$ とする.また, $\angle{\text{B}}$ の二等分線と線分 $\text{AP}$ ,辺 $\text{CA}$ との交点をそれぞれ $\text{Q},\text{R}$ とし,直線 $\text{CQ}$ と辺 $\text{AB}$ との交点を $\text{S}$ とする.このとき, $AS:SB$ を求めよ.
$\text{BC}=\sqrt{3^2+4^2}=5$
また, $\triangle{\mathrm{ABC}}\backsim\triangle{\mathrm{PBA}}$ より, $\text{BP}=\dfrac{9}{5}$,
$\triangle{\mathrm{ABC}}\backsim\triangle{\mathrm{PAC}}$ より, $\text{PC}=\dfrac{16}{5}$
よって, $BP:PC=9:16$ となる.一方, $CR:RA=BC:BA=5:3$ である.
チェバの定理より,
\begin{align} \frac{\text{BP}}{\text{PC}}\cdot\frac{\text{CR}}{\text{RA}}\cdot\frac{\text{AS}}{\text{SB}}&=1\\ \frac{9}{16}\cdot\frac{5}{3}\cdot\frac{\text{AS}}{\text{SB}}&=1\\ \frac{\text{AS}}{\text{SB}}&=\frac{16}{15}\\ AS:SB&=\boldsymbol{16:15} \end{align}メネラウスの定理
メネラウスの定理
メネラウスの定理
メネラウスの定理
無題
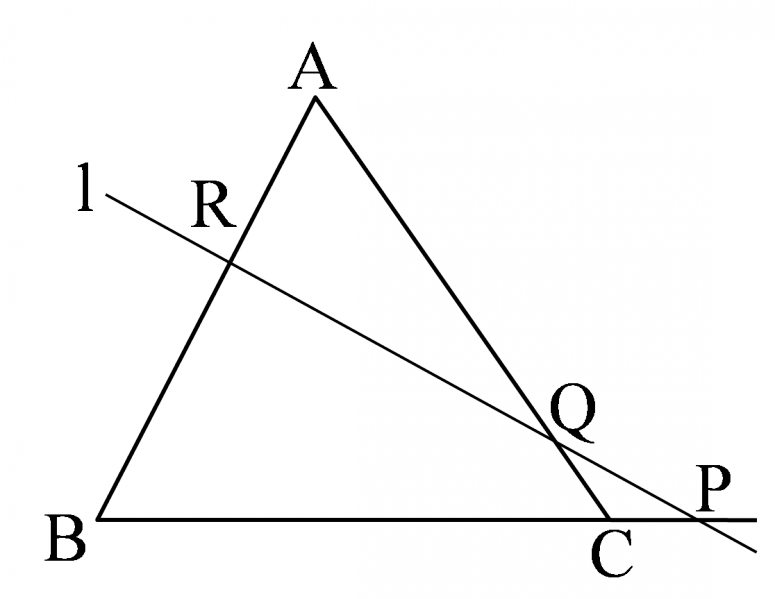
$\triangle{\mathrm{ABC}}$ の辺 $\mathrm{BC},\mathrm{CA},\mathrm{AB}$ またはその延長が,三角形の頂点を通らない直線 $\text{l}$ と,それぞれ点 $\mathrm{P},\mathrm{Q},\mathrm{R}$ で交わるとき
\[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}}=1\]証明
メネラウスの定理
無題
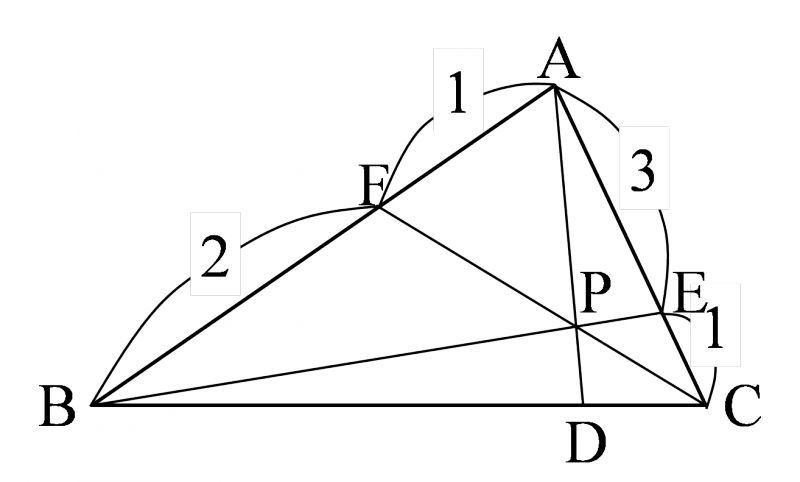
$\triangle{\mathrm{ABC}}$ において,辺 $\text{AC}$ を $3:1$ の比に内分する点を $\text{E}$ ,辺 $\text{AB}$ を $1:2$ の比に内分する点を $\text{F}$ とし, $\text{BE}$ と $\text{CF}$ の交点を $\text{P}$ , $\text{AP}$ と $\text{BC}$ の交点を $\text{D}$ とする.このとき,次のものを求めよ.
- $BD:DC$
- $AP:PD$
- $CP:PF$
- $\triangle{\mathrm{ABP}}:\triangle{\mathrm{ABC}}$
- チェバの定理より, \[\frac{\text{BD}}{\text{DC}}\cdot\frac{\text{CE}}{\text{EA}}\cdot\frac{\text{AF}}{\text{FB}}=1,\frac{\text{BD}}{\text{DC}}\cdot\frac{1}{3}\cdot\frac{1}{2}=1\]
- $\triangle{\mathrm{ADC}}$ と直線 $\text{BE}$ にメネラウスの定理を用いると, \[\frac{\text{DB}}{\text{BC}}\cdot\frac{\text{CE}}{\text{EA}}\cdot\frac{\text{AP}}{\text{PD}}=1,\frac{6}{7}\cdot\frac{1}{3}\cdot\frac{\text{AP}}{\text{PD}}=1\]
- $\triangle{\mathrm{ACF}}$ と直線 $\text{BE}$ にメネラウスの定理を用いると, \[\frac{\text{CP}}{\text{PF}}\cdot\frac{\text{FB}}{\text{BA}}\cdot\frac{\text{AE}}{\text{EC}}=1,\frac{\text{CP}}{\text{PF}}\cdot\frac{2}{3}\cdot\frac{3}{1}=1\]
- $AP:PD=7:2$ より, $\triangle{\mathrm{ABP}}=\dfrac{7}{9}\triangle{\mathrm{ABD}}$
よって,
\[BD:DC=\boldsymbol{6:1}\]よって,
\[AP:PD=\boldsymbol{7:2}\]よって,
\[CP:PF=\boldsymbol{1:2}\]$BD:DC=6:1$ より, $\triangle{\mathrm{ABD}}=\dfrac{6}{7}\triangle{\mathrm{ABC}}$
よって, $\triangle{\mathrm{ABP}}=\dfrac{7}{9}\times\dfrac{6}{7}\triangle{\mathrm{ABC}}=\dfrac{2}{3}\triangle{\mathrm{ABC}}$
ゆえに, $\triangle{\mathrm{ABP}}:\triangle{\mathrm{ABC}}=\boldsymbol{2:3}$
円と三角形
円周角の定理
円周角の定理
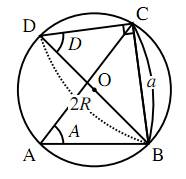
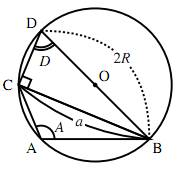
円周角の定理
無題
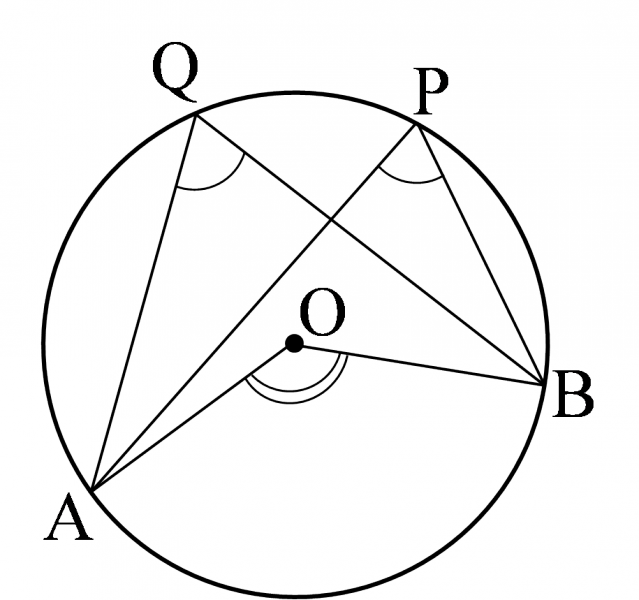
1つの弧に対する円周角の大きさは一定であり,その弧に対する中心角の大きさの半分である.
円周角の定理
次の図で, $\angle{x}$ の大きさを求めよ.
- $48^\circ$
- $132^\circ$
- $105^\circ$
- $112^\circ$
- $70^\circ$
- $50^\circ$
円周角の定理の逆
無題
4点 $\mathrm{A},\mathrm{B},\mathrm{P},\mathrm{Q}$ について,点 $\mathrm{P},\mathrm{Q}$ が直線 $\mathrm{AB}$ に関して同じ側にあって
\[\angle{\mathrm{APB}}=\angle{\mathrm{AQB}}\]ならば,4点 $\mathrm{A},\mathrm{B},\mathrm{P},\mathrm{Q}$ は1つの円周上にある.
円周角の定理の逆
次の図で, $\angle{x}$ の大きさを求めよ.
- $\angle{\text{ABD}}=\angle{\text{ACD}}=30^\circ$ より,
- $\angle{\text{CAD}}=180^\circ-(118^\circ+30^\circ)=32^\circ$
- $\angle{\text{CAD}}=42^\circ-27^\circ=15^\circ$
4点 $\text{A},\text{B},\text{C},\text{D}$ は同一円周上にある.
$\angle{\text{CBD}}=\angle{\text{CAD}}=40^\circ$ より,
$\triangle{\mathrm{BCD}}$ において,
\[\angle{x}=180^\circ-(40^\circ+81^\circ+30^\circ)=\boldsymbol{29^\circ}\]$\angle{\text{CAD}}=\angle{\text{CBD}}$ より,
4点 $\text{A},\text{B},\text{C},\text{D}$ は同一円周上にある.
\[\angle{x}=\angle{\text{ACD}}=\boldsymbol{30^\circ}\]$\angle{\text{CAD}}=\angle{\text{CBD}}$ より,
4点 $\text{A},\text{B},\text{C},\text{D}$ は同一円周上にある.
\begin{align} \angle{x}&=\angle{\text{ABD}}\\ &=180^\circ-(98^\circ+27^\circ+15^\circ)\\ &=\boldsymbol{40^\circ} \end{align}円に内接する四角形の定理
円に内接する四角形の定理
円に内接する四角形の定理
無題
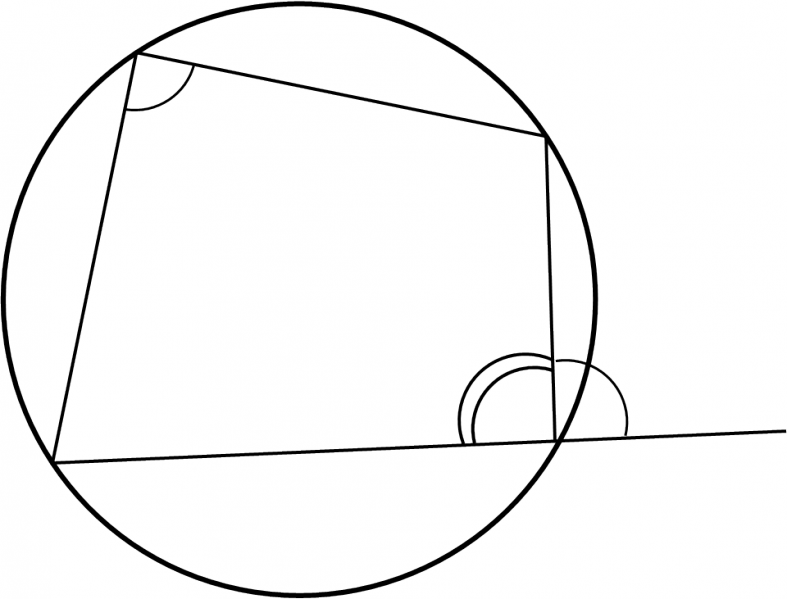
円に内接する四角形について,次の2つが成り立つ.
- 対角の和は $180^\circ$ である.
- 内角は,その対角の外角に等しい.
証明
円に内接する四角形の定理
次の図で, $\angle{x},\angle{y}$ の大きさを求めよ.
- \[\angle{x}=180^\circ-110^\circ=\boldsymbol{70^\circ},\angle{y}=\boldsymbol{120^\circ}\]
- $\angle{\text{BAD}}=180^\circ-100^\circ=80^\circ$ より, \[\angle{x}=180^\circ-(80^\circ+55^\circ)=\boldsymbol{45^\circ}\]
- \[\angle{x}=78^\circ\times2=\boldsymbol{156^\circ}\]
- $\angle{\text{CAD}}=86^\circ-52^\circ=34^\circ$ より, \[\angle{x}=180^\circ-34^\circ\times2=\boldsymbol{112^\circ}\]
- $\triangle{\text{ABC}}$ は $\text{AB}=\text{AC}$ の二等辺三角形だから, \[\angle{\text{ABC}}=(180^\circ-50^\circ)\times\frac{1}{2}=65^\circ\], \[\angle{x}=180^\circ-65^\circ=\boldsymbol{115^\circ}\]
- $\triangle{\text{OCD}}$ は $\text{OC}=\text{OD}$ の二等辺三角形だから, \[\angle{\text{COD}}=180^\circ-38^\circ\times2=104^\circ,\] \[\angle{x}=104^\circ\times\frac{1}{2}=\boldsymbol{52^\circ}\]
$\angle{\text{BCD}}=180^\circ-112^\circ=68^\circ$ より, $\triangle{\mathrm{BCD}}$ において,
\[\angle{y}=180^\circ-(52^\circ+68^\circ+38^\circ)=\boldsymbol{22^\circ}\]円と直線
円と直線の位置関係
円と直線の位置関係
| 円と直線の共有点の個数 | 2個 | 1個 | 0個 | |
| 円と直線の位置関係 |  |  |  |
円と接線
円と接線
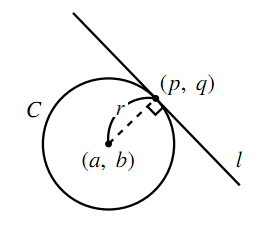
接弦定理
接弦定理
接弦定理
無題

円の接線とその接点を通る弦の作る角は,その内部にある弧に対する円周角に等しい.
接弦定理
次の図で, $\text{AT}$ は円の接線であり, $\text{A}$ はその接点である. $\angle{x}$ の大きさを求めよ.
- $\angle{x}=65^\circ$
- $\angle{x}=58^\circ\times2=\boldsymbol{116^\circ}$
- $\angle{x}=180^\circ-(68^\circ+36^\circ)=\boldsymbol{76^\circ}$
- $(\angle{x}+55^\circ)+102^\circ=180^\circ,\angle{x}=\boldsymbol{23^\circ}$
- $\angle{\text{BAT}}=\angle{\text{ACB}}=\angle{\text{ACD}}=26^\circ$ ,
- $\angle{\text{ABD}}=28^\circ,\angle{\text{BAD}}=90^\circ$ ,
$\angle{\text{ABD}}=\angle{\text{ACD}}=26^\circ$ より, $AT\parallel{DB}$
\begin{align} \angle{x}&=\angle{\text{CAT}}\\ &=180^\circ-(26^\circ+62^\circ)\\ &=\boldsymbol{92^\circ} \end{align}
$\angle{\text{ADB}}=\angle{x}+28^\circ$ より,
\begin{align} &28^\circ+90^\circ+(\angle{x}+28^\circ)=180^\circ,\\ &\angle{x}=\boldsymbol{34^\circ} \end{align}
方べきの定理
方べきの定理
方べきの定理
方べきの定理には,主に次の2つがある.
- 1つの円における2つの弦 $\mathrm{AB},\mathrm{CD}$ の交点,またはそれらの延長の交点を $\mathrm{P}$ とすると, \[\mathrm{PA}\cdot\mathrm{PB}=\mathrm{PC}\cdot\mathrm{PD}\]
- 円の外部の点 $\mathrm{P}$ から円に引いた接線の接点を $\mathrm{T}$ とする. $\mathrm{P}$ を通ってこの円と2点 $\mathrm{A},\mathrm{B}$ で交わる直線を引くと, \[\mathrm{PA}\cdot\mathrm{PB}=\mathrm{PT}^2\]
が成り立つ.
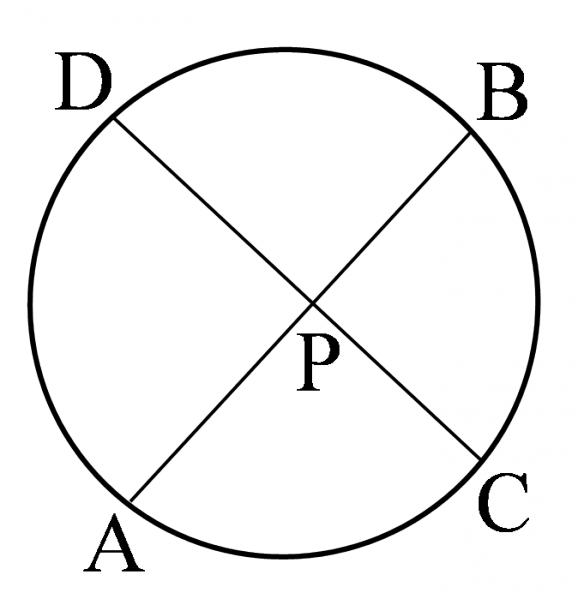

が成り立つ.

方べきの定理
次の図において, $x$ の値を求めよ.ただし,Tは円の接点とする.
- $4\cdot4=8x$ , $\boldsymbol{x=2}$
- $(x+6)\cdot{x}=5\cdot8,x^2+6x-40=0$
- $6\cdot10=x^2$
$x\gt0$ より, $\boldsymbol{x=4}$
$x\gt0$ より, $\boldsymbol{x=2\sqrt{15}}$
円と円
2円の位置関係
2円の位置関係
2円の位置関係は,2円の半径と中心間の距離で決まり,以下の5つの状態がある.
2円の位置関係
2円の半径を $r_1,r_2(r_1\lt r_2)$ ,中心間の距離を $d$ とすると,以下のようになる.
| 2円の図 |  |  |  | |
| 2円の位置関係 | 離れている | 外接している | 交わっている | |
| 2円の共有点の個数 | 0個 | 1個(外接) | 2個 | |
| 2円の中心間の距離 $d$ | $d\gt{r_1+r_2}$ | $d=r_1+r_2$ | $d\lt{r_1+r_2}$ |
| 2円の図 |  |  | |
| 2円の位置関係 | 内接している | 一方が他方を含む | |
| 2円の共有点の個数 | 1個(内接) | 0個 | |
| 2円の中心間の距離 $d$ | $d\gt{r_2-r_1}$ | $d\lt{r_2-r_1}$ |
2円の関係
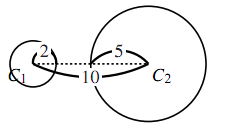
円 $C_1$ は $\text{A}$ を中心とした半径 $2$ の円,円 $C_2$ は $\text{B}$ を中心とした半径 $5$ の円とする.
- $\text{AB}=10$ のとき,円 $C_1$ と $C_2$ はどんな位置関係にあるか.また, $\text{AB}=6$ のとき, $\text{AB}=2$ のときはどうか.
- $C_1$ と $C_2$ が外接するとき線分 $\text{AB}$ の長さを求めよ.また,内接するときはどうか.
- $C_1$ が $C_2$ に含まれるための,線分 $\text{AB}$ の長さの条件を求めよ.
- $\text{AB}=10$ のときは共有点がない
- 外接のときは $\text{AB}=7$ ,内接のときは $\text{AB}=3$ .
- 線分 $\text{AB}$ の長さが,内接するときより短ければよいので, $(0\lt)\boldsymbol{\text{AB}\lt3}$ .
$\text{AB}=6$ のときは2点で交わる
$\text{AB}=2$ のときは円 $C_1$ が円 $C_2$ に含まれている
2円と共通接線
2円と共通接線
2円の共通接線の本数は,2円の位置関係によって異なる.
2円の共通接線
| 共通接線の本数 | 4本 | 3本 | 2本 | 1本 | 0本 | |
| 2円と共通接線の図 |  |  |  |  |  | |
| 2円の位置関係 | 離れている | 外接している | 交わっている | 内接している | 一方が他方を含む |
$\uparrow$ 2円の中心間を横切る共通接線は共通内接線(2本ある),2円の上下で接する共通接線は共通外接線(2本ある)と言われる.
共通接線の方程式を求めるには,問題を図示し,図形的に考えることが不可欠である.
2円と共通接線
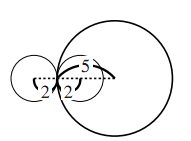
次の図で,直線 $\text{AB}$ は円 $\text{O}$ , $\text{O'}$ の共通接線で, $\text{A}$ , $\text{B}$ はその接点である.このとき,点 $\text{O'}$ から直線 $\text{OA}$ に垂線 $\text{O'A'}$ を引き, $\triangle{\mathrm{OO'A'}}$ を考えることにより,線分 $\text{AB}$ の長さを求めよ.
- \[\sqrt{13^2-(10-5)^2}=\boldsymbol{12}\]
- \[\sqrt{15^2-(8+4)^2}=\boldsymbol{9}\]





















