一般角と弧度法

FTEXT数学Iで学んだ三角比によって、さまざまな図形の辺の長さや角を計算で求めることができるようになった。この章では三角比を拡張した三角関数について学んでいこう。三角関数の応用範囲は広く、たとえばモーターの回転、ばねの伸縮、波の伝播などを数式で記述することができるようになる。まずは準備として、角度について新しい単位を導入していく。

一般角

動径

無題

平面上で，点 $\text{O}$ を中心として半直線 $\text{OP}$ を回転させるとき，この半直線 $\text{OP}$ を動径(radius vector) といい，はじめの固定された半直線 $\text{OX}$ を始線(initial line) という．

角度の拡張

固定された図形にあらわれる角度の大きさは， $0^\circ$ から $360^\circ$ である．この視点で見れば，時計の1時の長針と2時30分の長針のなす角度は $180^\circ$ であり，1時の長針と3時30分の長針のなす角度も $180^\circ$ である．しかし，時刻の変化に伴う長針の回転量は，前者と後者では明らかに異なる．また，長針を1時から10分進めても，10分戻してもどちらも $60^\circ$ 回転するが，向きは逆である．

これらの点を考慮できるように $360^\circ$ 以上の角や，回転の向きを考えた角を導入することにしよう．

1) $360^\circ$ 以上の角度

動点 $\text{P}$ は(反時計回りに)1周より多く動いてもよいとする．たとえば，図では， $\text{P}$ が反時計回りに１周と $60^\circ$ 回転しているので， $\angle{\text{POX}}=360^\circ+60^\circ=420^\circ$ と考える．

2) 負の角度

動点 $\text{P}$ は， $\text{X}$ から時計回りに動いてもよいとし，この場合は $\angle{\text{POX}}$ を負の値で定める．たとえば，図では， $\text{P}$ が時計回りに $120^\circ$ 回転しているので， $\angle{\text{POX}}=-120^\circ$ と考える．

これらのように， $360^\circ$ 以上回転する場合や，回転の向きも考えた角を 一般角(general angle) という．

また，一般角 $\theta$ に対して，始線 $\text{OX}$ から角 $\theta$ だけ回転した位置にある動径 $\text{OP}$ を， $\theta$ の動径という．

一般角の練習〜その1〜

次の図の $\theta$ を一般角で表せ．

一般角の練習〜その1〜の解答

動径 $\text{OP}$ は，反時計回りに1周と $120^\circ$ 進んだので
$\begin{align} \theta=360^\circ+120^\circ=\boldsymbol{480^\circ} \end{align}$
動径 $\text{OP}$ は，反時計回りに2周と $210^\circ$ 進んだので
← $360^\circ-150^\circ=210^\circ$
$\begin{align} \theta=360^\circ\times2+210^\circ=\boldsymbol{930^\circ} \end{align}$
動径 $\text{OP}$ は，時計回りに $300^\circ$ 進んだので
← $360^\circ-60^\circ=300^\circ$
$\begin{align} \theta=\boldsymbol{-300^\circ} \end{align}$

一般角の練習〜その2〜

次の角の動径を図示せよ．

$150^\circ$
$390^\circ$
$-90^\circ$
$-690^\circ$

一般角の練習〜その２〜の解答

動径の表す角

無題

動径の表す角

動径は $360^\circ$ 回転するともとの位置に戻るので，たとえば， $60^\circ$ の動径は，図のように

$\begin{align} &420^\circ~(~=60^\circ+360^\circ)\\ &780^\circ~(~=60^\circ+360^\circ\times2)\\ &-300^\circ~(~=60^\circ-360^\circ) \end{align}$

などの角の動径と同じ位置にくる．すなわち， $60^\circ+360^\circ\times n$ ( $n$ は整数)の動径はすべて同じ位置にくる．これらの角を動径 $\text{OP}$ の表す角という．

一般に，次のことがいえる．

動径の表す角

動径 $\text{OP}$ と始線 $\text{OX}$ のなす角の1つを $\alpha$ とすると，動径 $\text{OP}$ の表す角 $\theta$ は

$\begin{align} \theta=\alpha+360^\circ\times n \end{align}$ (

$n$ は整数)

のようにあらわされる．

動径の表す角

次の角の動径を $\text{OP}$ とするとき，動径 $\text{OP}$ の表す角を

$\begin{align} \alpha+360^\circ\times n \end{align}$ (

$n$ は整数)

の形で表せ．ただし， $0^\circ\leqq\alpha<360^\circ$ とする．

$420^\circ$
$1450^\circ$
$-80^\circ$
$-895^\circ$

動径の表す角の解答

$420^\circ=360^\circ\times1+60^\circ$ なので $\boldsymbol{60^\circ+360^\circ\times n}$
$1450^\circ=360^\circ\times4+10^\circ$ なので $\boldsymbol{10^\circ+360^\circ\times n}$
$-80^\circ=360^\circ\times(-1)+280^\circ$ なので $\boldsymbol{280^\circ+360^\circ\times n}$
$-895^\circ=360^\circ\times(-3)+185^\circ$ なので $\boldsymbol{185^\circ+360^\circ\times n}$

弧度法

度数法の問題点

（注）（注）

度数法の問題点

これまで，角度の大きさは「1周は $360^\circ$ 」と定義して表してきた．この方法は度数法(degree measure) と呼ばれ，紀元前から用いられてきたものである．しかし，度数法で表わされた角の値は便宜的なもので数学的根拠がなく，数学の発展と共に不便が生じてきた．

弧度法の定義

そこで，これらの不便を解消するための新しい角度を導入しよう．

弧度法

無題

（注）

弧の長さが $l$ ,半径が $r$ の円弧のなす中心角 $\theta$ を

$\begin{align} \theta=\dfrac{l}{r} \end{align}$

で定義する．

このような角度の表し方を弧度法(circular measure) という．弧度法は比で角度の大きさを表すため，単位が無いが，あえて単位を付けたいときにはラジアン(radian) や弧度をもちいる．

無題

上の定義において， $r = 1$ とすると $\theta = l$ となる．これは，単位円で考えたときには，中心角は対応する弧の長さで表されることを意味している．すなわち

$\begin{align} 360^\circ=2\pi \end{align}$ ラジアン

である．

主な角について，度数法と弧度法の値をまとめると次のようになる．

度数法		$0^\circ$	$30^\circ$	$45^\circ$	$60^\circ$	$90^\circ$	$120^\circ$
弧度法		$0$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$	$\dfrac{2}{3}\pi$

度数法		$135^\circ$	$150^\circ$	$180^\circ$	$270^\circ$	$360^\circ$
弧度法		$\dfrac{3}{4}\pi$	$\dfrac{5}{6}\pi$	$\pi$	$\dfrac{3}{2}\pi$	$2\pi$

弧度法についても動径の表す角について，次のことがいえる．

弧度法での動径の表す角

動径 $\text{OP}$ と始線 $\text{OX}$ のなす角の1つを $\alpha$ とすると，動径 $\text{OP}$ の表す角 $\theta$ は

$\begin{align} \theta=\alpha+2n\pi \end{align}$ (

$n$ は整数)

のようにあらわされる．

度数法を弧度法になおす

次の角を弧度法で表せ．また， $\alpha + 2n \pi$ ( $n$ は整数)の形で表せ．ただし， $0\leqq\alpha<2\pi$ とする．

$15^\circ$
$550^\circ$
$80^\circ$
$-570^\circ$

度数法を弧度法になおすの解答

$\boldsymbol{\dfrac{\pi}{12}},\boldsymbol{\dfrac{\pi}{12}+2n\pi}$
$\boldsymbol{\dfrac{55}{18}\pi},\boldsymbol{\dfrac{19}{18}\pi+2n\pi}$
$\boldsymbol{\dfrac{4}{9}\pi},\boldsymbol{\dfrac{4}{9}\pi+2n\pi}$
$\boldsymbol{-\dfrac{19}{6}\pi},\boldsymbol{\dfrac{5}{6}\pi+2n\pi}$

弧度法を度数法になおす

次の角を度数法で表せ．

$8\pi$
$-\dfrac{7}{3}\pi$
$-\dfrac{43}{12}\pi$
$-\dfrac{21}{10}\pi$

弧度法を度数法になおすの解答

$\boldsymbol{1440^\circ}$
$\boldsymbol{-420^\circ}$
$\boldsymbol{-645^\circ}$
$\boldsymbol{-378^\circ}$

扇形の弧の長さと面積

無題

扇形の弧の長さと面積

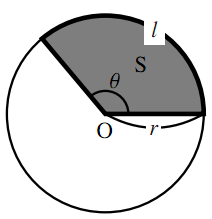
扇形の弧の長さと面積を，弧度法をもちいて表してみよう．

図のように半径が $r$ ,中心角が $\theta$ の扇形の弧の長さを $l$ ,面積を $\text{S}$ とすると，弧度法の定義より $\theta=\dfrac{l}{r}$ だから

$\begin{align} \therefore~&l=r\theta \end{align}$

$\tag{1}\label{ougigatanokononagasatomenseki1}$

面積と中心角の比から

$\begin{align} \qquad{\text{S}}:\theta=\pi r^2:2\pi \end{align}$

$\begin{align} \therefore~&\text{S}=\dfrac{1}{2}r^2\theta \end{align}$

$\tag{2}\label{ougigatanokononagasatomenseki2}$

以上， $\eqref{ougigatanokononagasatomenseki1}$ ， $\eqref{ougigatanokononagasatomenseki2}$ より， $\text{S}=\dfrac{1}{2}rl$ となる．

扇形の弧の長さと面積

無題

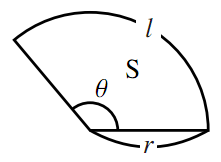
半径が $r$ ,中心角が $\theta$ の扇形の弧の長さを $l$ ,面積を $\text{S}$ とすると

$\begin{align} &l=r\theta\\ &\text{S}=\dfrac{1}{2}r^2\theta=\dfrac{1}{2}rl \end{align}$

である．

吹き出し扇形の弧の長さと面積

無題

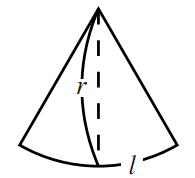
図のように，扇形を，あたかも底辺が $l$ ,高さが $r$ の三角形のように考え， (底辺) $\times$ (高さ) $\div 2$ から， $\text{S}=\dfrac{1}{2}rl$ と覚えておけばよい．

扇形の弧の長さと面積

次のような扇形の弧の長さ $l$ と面積 $\text{S}$ を求めよ．

半径が $9$ ，中心角が $\dfrac{2}{3}\pi$
半径が $3$ ，中心角が $\dfrac{\pi}{5}$

扇形の弧の長さと面積の解答

$l=9\times\dfrac{2}{3}\pi=\boldsymbol{6\pi},$
$\text{S}=\dfrac{1}{2}\times9\times6\pi=\boldsymbol{27\pi}$
$l=3\times\dfrac{\pi}{5}=\boldsymbol{\dfrac{3}{5}\pi},$
$\text{S}=\dfrac{1}{2}\times3\times\dfrac{3}{5}\pi=\boldsymbol{\dfrac{9}{10}\pi}$