三角関数について

FTEXT数学Iの三角比で使う角度$\theta$は$0\leqq\theta\lt2\pi$だったが、ここからは、扱う角を任意の実数にまで拡張した三角関数についてみていくことにする。

三角関数の定義

三角関数の定義について

三角関数の定義について

FTEXT 数学Iで学んだ三角比(trigonometric ratio) で扱う角を任意の実数 とすれば，次の三角関数(trigonometric function) の定義となる．

三角関数の定義

無題
無題

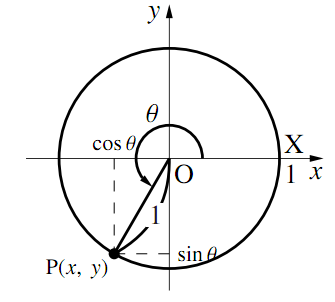
単位円周と動径の交点を$\text{P},\text{X}(1,~0)$とする．

$\angle{\text{POX}}=\theta$($\theta$は任意の実数)とするとき

$\cos\theta = $(動点$\text{P}$の$x$座標)

$\sin\theta = $(動点$\text{P}$の$y$座標)

$\tan\theta =$ (動点$\text{P}$の$y$座標)$/$(動点$\text{P}$の$x$座標)$=$(動径$\text{OP}$の傾き)

とする． ただし，動点$\text{P}$の$x$座標が$0$のとき， つまり$\theta=\dfrac{\pi}{2} +n\pi$($n$は整数) のときは$\tan\theta$は定義されない．

（注） （注）

具体的な例で確認してみよう．

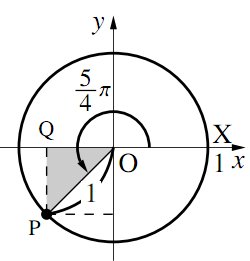
三角関数の定義についての図その１

1)$\theta=\dfrac{5}{4}\pi$のとき

$\triangle{\text{OPQ}}$は$\text{PQ}:\text{QO}:\text{OP}=1:1:\sqrt{2}$の直角三角形である．つまり，$\text{P}\left(-\dfrac{\sqrt{2}}{2},~-\dfrac{\sqrt{2}}{2}\right)$なので

\begin{align} &\cos\dfrac{5}{4}\pi=-\dfrac{\sqrt{2}}{2},~~~\\ &\sin\dfrac{5}{4}\pi=-\dfrac{\sqrt{2}}{2},~~~\\ &\tan\dfrac{5}{4}\pi=1 \end{align}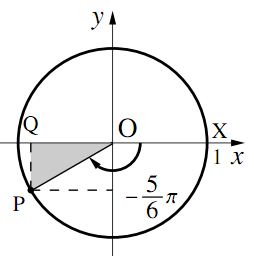
三角関数の定義についての図その２

2)$\theta=-\dfrac{5}{6}\pi$のとき

$\triangle{\text{OPQ}}$は$\text{PQ}:\text{QO}:\text{OP}=1:\sqrt{3}:2$の直角三角形である．つまり，$\text{P}\left(-\dfrac{\sqrt{3}}{2},~-\dfrac{1}{2}\right)$なので

\begin{align} &\cos\left(-\dfrac{5}{6}\pi\right)=-\dfrac{\sqrt{3}}{2},~~~\\ &\sin\left(-\dfrac{5}{6}\pi\right)=-\dfrac{1}{2},~~~\\ &\tan\left(-\dfrac{5}{6}\pi\right)=\dfrac{1}{\sqrt{3}} \end{align}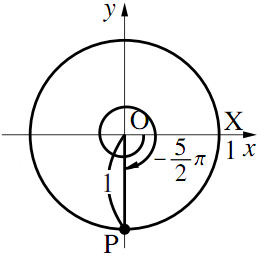
三角関数の定義についての図その３

3)$\theta=-\dfrac{5}{2}\pi$のとき

$-\dfrac{5}{2}\pi=-\dfrac{1}{2}\pi -2\pi$より， $\text{X}$から負の方向へ$-\dfrac{1}{2}\pi$移動した$(0,~-1)$に$\text{P}$があるので

\begin{align} &\cos\left(-\dfrac{5}{2}\pi\right)=0,~\\ &\sin\left(-\dfrac{5}{2}\pi\right)=-1,~\\ &\tan\left(-\dfrac{5}{2}\pi\right) \end{align} は定義できない

$\tan\theta$には次のような意味もあることを理解しておこう．

$\tan\theta$の図形的意味

無題
無題

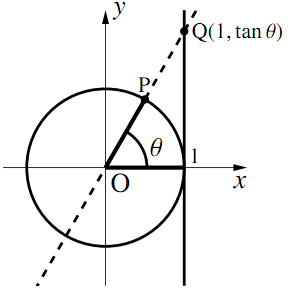
$\tan\theta$の定義は，動径$\text{OP}$の傾きであるが，傾きとは$x$軸方向に$1$増加するときの$y$軸方向の増加量である． そのため，図のように直線$\text{OP}$と直線$x = 1$の交点を$\text{Q}$とすると，$\text{Q}$の$y$座標が$\tan\theta$になる．

三角関数の定義域と値域

三角関数の定義域と値域

以上のことから，三角関数の定義域と値域は次のようにまとめられる．

三角関数の定義域と値域

  1. 三角関数の定義域

    1. $\sin\theta,\cos\theta$の$\theta$は，任意の実数をとることができる．

    2. $\tan\theta$の$\theta$は，$\dfrac{\pi}{2}+n\pi$($n$は整数)以外の任意の実数をとることができる．

  2. 三角関数の値域

    1. 任意の実数$\theta$に対し，$\sin\theta,\cos\theta$は$ − 1$以上$1$以下の値をとる．

    2. $\dfrac{\pi}{2}+n\pi$($n$は整数)以外の任意の実数$\theta$に対し，$\tan\theta$は任意の実数をとる．

三角関数の符号と動径の象限

三角関数の符号と動径の象限

三角関数の値の符号は，その角の動径がどの象限に含まれるかで決定する． まとめると次のようになる．

三角関数の符号と動径の象限

三角関数の値の符号は，動径のある象限によって次のように決まる．

1)$\sin\theta$の符号

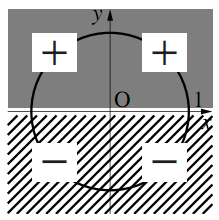
三角関数の符号と動径の象限の図その１

2)$\cos\theta$の符号

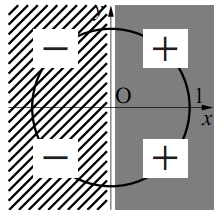
三角関数の符号と動径の象限の図その２

3)$\tan\theta$の符号

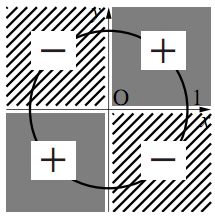
三角関数の符号と動径の象限の図その３

任意の角に対する三角関数の値

以下の角度に対する，正弦，余弦，正接の値をそれぞれ求めよ．

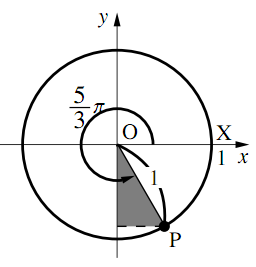
  1. $\dfrac{5}{3}\pi$
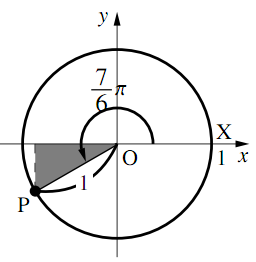
  2. $\dfrac{7}{6}\pi$
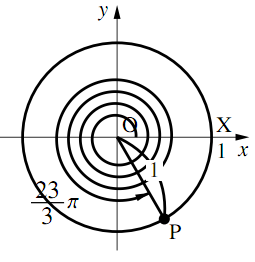
  3. $\dfrac{23}{3}\pi$
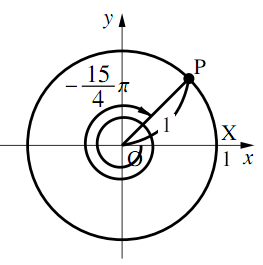
  4. $-\dfrac{15}{4}\pi$

    任意の角に対する三角関数の値の解答の図その１


  1. $\text{P}~\left(\dfrac{1}{2},~-\dfrac{\sqrt{3}}{2}\right)$なので

    $\boldsymbol{\cos\dfrac{5}{3}\pi=\dfrac{1}{2}}$

    $\boldsymbol{\sin\dfrac{5}{3}\pi=-\dfrac{\sqrt{3}}{2}}$

    $\boldsymbol{\tan\dfrac{5}{3}\pi=-\sqrt{3}}$

    2. 任意の角に対する三角関数の値の解答の図その２


  2. $\text{P}~\left(-\dfrac{\sqrt{3}}{2},~ -\dfrac12\right)$なので

    $\boldsymbol{\cos\dfrac{7}{6}\pi=-\dfrac{\sqrt{3}}{2}}$

    $\boldsymbol{\sin\dfrac{7}{6}\pi=-\dfrac{1}{2}}$

    $\boldsymbol{\tan\dfrac{7}{6}\pi=\dfrac{\sqrt{3}}{3}}$

    3. 任意の角に対する三角関数の値の解答の図その３


  3. $\dfrac{23}{3}\pi=\dfrac{5}{3}\pi +3\cdot 2\pi$より，$\dfrac{5}{3}\pi$の三角関数に等しい．1.より

    $\boldsymbol{\cos\dfrac{23}{3}\pi=\dfrac{1}{2}}$

    $\boldsymbol{\sin\dfrac{23}{3}\pi=-\dfrac{\sqrt{3}}{2}}$

    $\boldsymbol{\tan\dfrac{23}{3}\pi=-\sqrt{3}}$

    4. 任意の角に対する三角関数の値の解答の図その４


  4. $-\dfrac{15}{4}\pi=\dfrac{1}{4}\pi +(-2)\cdot 2\pi$より，$\dfrac{1}{4}\pi$の三角関数に等しい．よって

    $\boldsymbol{\cos\left(-\dfrac{15}{4}\pi\right)=\dfrac{\sqrt{2}}{2}}$

    $\boldsymbol{\sin\left(-\dfrac{15}{4}\pi\right)=\dfrac{\sqrt{2}}{2}}$

    $\boldsymbol{\tan\left(-\dfrac{15}{4}\pi\right)=1}$

三角関数を含む方程式

  1. $0\leqq \theta<2\pi$のとき，$\sin\theta =-\dfrac{1}{2}$を満たす$\theta$を求めよ．
  2. $0\leqq \theta<4\pi$のとき，$\sin\theta =-\dfrac{1}{2}$を満たす$\theta$を求めよ．
  3. $\theta$を任意の実数とする．$\sin\theta =-\dfrac{1}{2}$を満たす$\theta$を求めよ．
  4. $-\pi\leqq \theta<\pi$のとき，$\sin\theta =-\dfrac{1}{2}$を満たす$\theta$を求めよ．

無題
無題

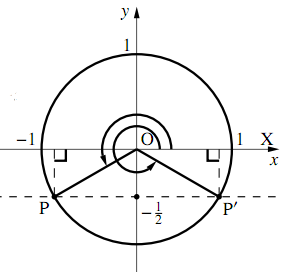
(動点の$y$座標の値)$=-\dfrac{1}{2}$であればよいので，求める$\theta$は，図の$\angle{\text{POX}},~\angle{\text{P}’\text{OX}}$に等しい．

  1. $0\leqq \theta < 2\pi$の範囲では

    $\angle{\text{POX}}=\dfrac{7}{6}\pi,~~$

    $\angle{\text{P}’\text{OX}}=\dfrac{11}{6}\pi$

    となる．つまり，$\boldsymbol{\theta=\dfrac{7}{6}\pi,~\dfrac{11}{6}\pi}$．

  2. $0\leqq \theta < 4\pi$の範囲では

    \begin{align} &\angle{\text{POX}}=\dfrac{7}{6}\pi,~\dfrac{7}{6}\pi +2\pi\\ &\angle{\text{P}’\text{OX}}=\dfrac{11}{6}\pi,~\dfrac{11}{6}\pi +2\pi \end{align}

    となる．つまり，

    $\boldsymbol{\theta=\dfrac{7}{6}\pi,~\dfrac{11}{6}\pi,~\dfrac{19}{6}\pi,~\dfrac{23}{6}\pi}$．

  3. $\theta$は任意なので，$n$を整数として

    \begin{align} &\angle{\text{POX}}=\dfrac{7}{6}\pi +2n\pi,~~\\ &\angle{\text{P}’\text{OX}}=\dfrac{11}{6}\pi +2n\pi \end{align}

    となる．つまり，$ \boldsymbol{\theta=\dfrac{7}{6}\pi +2n\pi,~\dfrac{11}{6}\pi +2n\pi}$．

  4. $-\pi\leqq \theta < \pi$の範囲では

    \begin{align} &\angle{\text{POX}}=\dfrac{7}{6}\pi -2\pi,~~\\ &\angle{\text{P}’\text{OX}}=\dfrac{11}{6}\pi -2\pi \end{align}

    となる．つまり， $\boldsymbol{\theta=-\dfrac{5}{6}\pi,~ -\dfrac{1}{6}\pi}$．

三角関数を含む不等式

  1. $0\leqq \theta<2\pi$のとき，$\cos\theta <\dfrac{1}{2}$を満たす$\theta$の範囲を求めよ．
  2. $0\leqq \theta<4\pi$のとき，$\cos\theta <\dfrac{1}{2}$を満たす$\theta$の範囲を求めよ．
  3. $\theta$を任意の実数とする．$\cos\theta <\dfrac{1}{2}$を満たす$\theta$の範囲を求めよ．
  4. $-\pi\leqq \theta<\pi$のとき，$\cos\theta <\dfrac{1}{2}$を満たす$\theta$の範囲を求めよ．

無題
無題

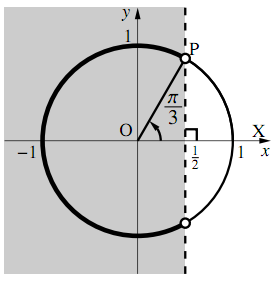
(動点の$x$座標の値)$<\dfrac{1}{2}$であればよい．

そのためには，動点が図の太線部分にあればよい．

  1. $0\leqq \theta < 2\pi$の範囲では， $\boldsymbol{\dfrac{1}{3}\pi<\theta<\dfrac{5}{3}\pi}$．

  2. $0\leqq \theta < 4\pi$の範囲では， 1.の答えに加えて

    $\dfrac{1}{3}\pi +2\pi <\theta<\dfrac{5}{3}\pi +2\pi$

    も満たすので， $\boldsymbol{\dfrac{1}{3}\pi <\theta<\dfrac{5}{3}\pi,~\dfrac{7}{3}\pi <\theta<\dfrac{11}{3}\pi}$．

  3. $\theta$は任意なので，

    $\boldsymbol{\dfrac{1}{3}\pi +2n\pi <\theta<\dfrac{5}{3}\pi +2n\pi~~}$($n$は整数)

    が求める答えとなる．

  4. $-\pi\leqq \theta < \pi$の範囲では

    \begin{align} -\pi \leqq \theta<\dfrac{5}{3}\pi -2\pi,~~ \dfrac{1}{3}\pi <\theta< \pi \end{align}

    となる．つまり， $\boldsymbol{-\pi \leqq \theta<-\dfrac{1}{3}\pi,~ \dfrac{1}{3}\pi <\theta<\pi}$．

範囲をもつ変数の置き換え

  1. $0\leqq \theta <2\pi,~\theta'=2 \theta -\dfrac{\pi}{3}$とする． $\theta'$のとりうる範囲を求めよ．
  2. $0\leqq \theta <2\pi$のとき， 方程式$\sin\left(2 \theta -\dfrac{\pi}{3}\right) =\dfrac{\sqrt{3}}{2}$を満たす$\theta$の値を求めよ．
  3. $0\leqq \theta <2\pi$のとき， 不等式$\sin\left(2 \theta -\dfrac{\pi}{3}\right) <\dfrac{\sqrt{3}}{2}$を満たす$\theta$の範囲を求めよ．

  1. \begin{align} &0\leqq \theta <2\pi\\ \Leftrightarrow~&0\leqq 2\theta <4\pi\\ \Leftrightarrow~&0-\dfrac{\pi}{3} \leqq 2\theta-\dfrac{\pi}{3} <4\pi-\dfrac{\pi}{3} \end{align}

    より$\boldsymbol{-\dfrac{\pi}{3} \leqq \theta' <\dfrac{11}{3}\pi}$と分かる．

    ←$2$倍しても，$\dfrac{\pi}{3}$を引いても大小関係は変わらない

    2. 範囲をもつ変数の置き換えの解答の図その１

  2. 1.の$ \theta'$を用いると，与えられた方程式は$\sin\theta' =\dfrac{\sqrt{3}}{2}$となる． 1.より$-\dfrac{\pi}{3} \leqq \theta' <\dfrac{11}{3}\pi$なので，図より

    $\theta' =\dfrac13\pi,~\dfrac23\pi,~\dfrac73\pi,~\dfrac83\pi$となる．

    $\theta=\dfrac{\theta'}{2}+\dfrac{\pi}{6}$なので

    \begin{align} \boldsymbol{\theta= \dfrac13\pi,~\dfrac12\pi,~\dfrac43\pi,~\dfrac32\pi} \end{align}
    3. 範囲をもつ変数の置き換えの解答の図その２

  3. 1.の$ \theta'$を用いると，与えられた不等式は$\sin\theta' <\dfrac{\sqrt{3}}{2}$となる． 1.より$-\dfrac{\pi}{3} \leqq \theta' <\dfrac{11}{3}\pi$なので

    $-\dfrac{\pi}{3}\leqq \theta' <\dfrac13\pi,~\dfrac23\pi< \theta' <\dfrac73\pi,$
    $~\dfrac83\pi< \theta' <\dfrac{11}{3}\pi$となる．$ \theta'=2\theta-\dfrac{\pi}{3}$を代入して$\theta$について解けば

    ←たとえば

    \begin{align} &\dfrac{2}{3}\pi< 2\theta-\dfrac{\pi}{3} <\dfrac{7}{3}\pi\\ \Leftrightarrow~&\pi< 2\theta<\dfrac83\pi ~\Leftrightarrow~\dfrac{\pi}{2}< \theta<\dfrac{4}{3}\pi \end{align} \begin{align} &\boldsymbol{0\leqq\theta< \dfrac{\pi}{3},~\dfrac{\pi}{2}<\theta<\dfrac43\pi,}\\ &\boldsymbol{\dfrac32\pi<\theta <2\pi} \end{align}

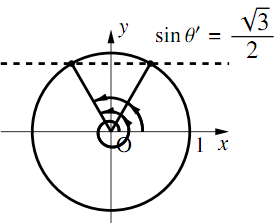
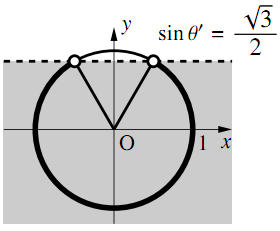
三角関数の相互関係

三角関数の相互関係について

三角関数の相互関係について

三角関数においても，FTEXT 数学Iで学んだ三角比の相互関係

\begin{align} &\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}},\sin^2{\theta}+\cos^2{\theta}=1,\\ &1+\dfrac{1}{\tan^2{\theta}}=\dfrac{1}{\sin^2{\theta}},\tan^2{\theta}+1=\dfrac{1}{\cos^2{\theta}} \end{align}

が成り立つ．

拡張された三角関数の相互関係

任意の実数$\theta$について，次の式が成り立つ(ただし，分母が$0$となる場合を除く)．

1)$\sin\theta,\cos\theta,\tan\theta$の関係

\begin{align} \tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}} \end{align}

2)$\sin\thetaと\cos\theta$の関係

\begin{align} \sin^2{\theta}+\cos^2{\theta}=1 \end{align}

3)$\tan\thetaと\sin\theta$の関係

\begin{align} 1+\dfrac{1}{\tan^2{\theta}}=\dfrac{1}{\sin^2{\theta}} \end{align}

4)$\cos\thetaと\tan\theta$の関係

\begin{align} \tan^2{\theta}+1=\dfrac{1}{\cos^2{\theta}} \end{align}

吹き出し三角関数の相互関係について

3)と4)は記憶しなくても，1)と2)からすぐに導ける． 2)の両辺を$\sin^2\theta$や$\cos^2\theta$で割って作ればよい，ということだけ覚えておこう．

三角関数の相互関係の利用

  1. $\cos{\theta}=\dfrac{1}{3}$のとき，以下の問いに答えなさい．

    1. $0 < \theta < \pi$のとき，$\sin{\theta},~\tan{\theta}$の値を求めなさい．

    2. $-\dfrac{\pi}{2}<{\theta}<\dfrac{\pi}{2}$のとき，$\sin{\theta},~\tan{\theta}$の値を求めなさい．

  2. $\pi<{\theta}<2\pi,~\tan{\theta}=2$のとき，$\cos{\theta},~\sin{\theta}$の値を求めなさい．

  1. $\sin^2{\theta}=1-\cos^2{\theta}=\dfrac{8}{9}$より，$\sin{\theta}=\pm\dfrac{2\sqrt{2}}{3}$．

    ←拡張された三角関数の相互関係

    1. $0 < \theta < \pi$より，$\sin\theta > 0$なので

      $\boldsymbol{\sin{\theta}=\dfrac{2\sqrt{2}}{3}}$．また，$\tan{\theta}=\dfrac{\dfrac{2\sqrt{2}}{3}}{\dfrac{1}{3}}=\boldsymbol{2\sqrt{2}}$．

      ←拡張された三角関数の相互関係

    2. $-\dfrac{\pi}{2}<{\theta}<\dfrac{\pi}{2}$より$\sin\theta$は正負どちらでもよい． よって$\boldsymbol{\sin{\theta}=\pm\dfrac{2\sqrt{2}}{3}}$,$\tan{\theta}=\dfrac{\pm2\sqrt{2}/3}{1/3}=\boldsymbol{\pm 2\sqrt{2}}$．

  2. $\dfrac{1}{\cos^2{\theta}}=1+\tan^2{\theta}=5$より，$\cos{\theta}=\pm\sqrt{\dfrac{1}{5}}$．

    ←拡張された三角関数の相互関係

    ここで，$\pi<{\theta}<2\pi,~\tan{\theta}>0$より$\theta$は第$3$象限の角に対応し，$\cos\theta < 0$． よって，$\boldsymbol{\cos{\theta}=-\dfrac{1}{\sqrt{5}}}$．

    また，$\sin{\theta} =\tan{\theta}\cos{\theta}=2\times \dfrac{1}{\sqrt{5}}=\boldsymbol{-\dfrac{2}{\sqrt{5}}}$．

    ←拡張された三角関数の相互関係

$\sin\theta±\cos\theta$と$\sin\theta\cos\theta$の関係

    1. $\cos{\theta} +\sin{\theta}=\dfrac{1}{2}$のとき，$\sin{\theta}\cos{\theta}$,$\sin{\theta} -\cos{\theta}$の値を求めなさい．

    2. さらに，$0 < \theta < \pi$であるとき，$\sin{\theta},~ \cos{\theta}$の値を求めなさい．

  2. $-\dfrac{\pi}{2}<{\theta}<\dfrac{\pi}{2}$,$\cos{\theta}\sin{\theta}=\dfrac{1}{3}$のとき，$\sin{\theta},~ \cos{\theta}$の値を求めなさい．

    1. $\cos{\theta} +\sin{\theta}=\dfrac{1}{2}$の両辺を$2$乗して

      \begin{align} &1+2\cos{\theta}\sin{\theta}=\dfrac14 \\ ~~\Leftrightarrow~~&\boldsymbol{\cos{\theta}\sin{\theta}=-\dfrac{3}{8}} \end{align}

      ←拡張された三角関数の相互関係

      また，この値を代入すれば，

      \begin{align} &(\cos{\theta} -\sin{\theta})^2\\ &=1-2\cos{\theta}\sin{\theta}\\ &=\dfrac{7}{4} \end{align}

      よって，$\boldsymbol{\cos{\theta} -\sin{\theta}=\pm\dfrac{\sqrt{7}}{2}}$．

    2. 1.より，次の連立方程式が成立する．

      \begin{cases} \cos{\theta} +\sin{\theta}=\dfrac{1}{2}\\ \cos{\theta} -\sin{\theta}=\pm\dfrac{\sqrt{7}}{2} \end{cases}

      上の式を$\tag{1}\label{sinshi-ta+-cosshi-tatosinshi-tacosshi-tanokankei1}$，下の式を$\tag{2}\label{sinshi-ta+-cosshi-tatosinshi-tacosshi-tanokankei2}$とすると，$\eqref{sinshi-ta+-cosshi-tatosinshi-tacosshi-tanokankei1}-\eqref{sinshi-ta+-cosshi-tatosinshi-tacosshi-tanokankei2}$より$2\sin{\theta}=\dfrac{1\mp\sqrt{7}}{2} $であるが，$0 < \theta < \pi$より$\sin\theta > 0$なので，$\boldsymbol{\sin{\theta}=\dfrac{1+\sqrt{7}}{4}}$． つまり，$\cos{\theta} -\sin{\theta}=-\dfrac{\sqrt{7}}{2}$と分かるので， $\eqref{sinshi-ta+-cosshi-tatosinshi-tacosshi-tanokankei1}+\eqref{sinshi-ta+-cosshi-tatosinshi-tacosshi-tanokankei2}$より $\boldsymbol{\cos{\theta}=\dfrac{1-\sqrt{7}}{4}}$となる．

  2. まず，$\cos{\theta} \pm \sin{\theta}$の$2$乗をそれぞれ考えて

    \begin{align} &(\cos{\theta}+\sin{\theta})^2\\ &=1+2\cos{\theta}\sin{\theta}=\dfrac53\\ &(\cos{\theta}-\sin{\theta})^2\\ &=1-2\cos{\theta}\sin{\theta}=\dfrac13\\ \Leftrightarrow~& \cos{\theta}+\sin{\theta}=\pm\dfrac{\sqrt{15}}{3},\\ &\cos{\theta}-\sin{\theta}=\pm\dfrac{\sqrt{3}}{3} \end{align}

    ←拡張された三角関数の相互関係

    である．ここで，$-\dfrac{\pi}{2}<{\theta}<\dfrac{\pi}{2}$より$\cos\theta > 0． \cos\theta\sin\theta > 0$なので$\sin\theta > 0$と分かる．

    よって，$\cos{\theta}>0,~\sin{\theta}>0$から$\cos\theta + \sin\theta > 0$．

    \begin{cases} \cos{\theta} +\sin{\theta}=\dfrac{\sqrt{15}}{3}\\ \cos{\theta} -\sin{\theta}=\pm\dfrac{\sqrt{3}}{3} \end{cases}

    この連立方程式を解いて（複合同順）

    $\boldsymbol{\left(\cos{\theta},~\sin{\theta}\right)}$
    $\boldsymbol{=\left(\dfrac{\sqrt{15}\pm\sqrt{3}}{6},~\dfrac{\sqrt{15}\mp\sqrt{3}}{6}\right)}$

三角関数の性質

$\theta+2n\pi$の三角関数

$\pi+2n\pi$の三角関数

$n$が整数のとき，角$\theta+2n\pi$の動径は，角$\theta$の動径と一致するので，次の公式が成り立つ．

$\pi+\theta$の三角比

任意の角$\theta$について

\begin{align} &\sin(\theta+2n\pi)=\sin\theta\\ &\cos(\theta+2n\pi)=\cos\theta\\ &\tan(\theta+2n\pi)=\tan\theta \end{align}

が成り立つ．ただし，$n$は整数とする．

$-\theta$の三角関数

$-\theta$の三角関数

暗記$-\theta$の三角関数

$\sin(-\theta),\cos(-\theta),\tan(-\theta)$を，それぞれ$\sin\theta,\cos\theta,\tan\theta$で表せ．

無題
無題

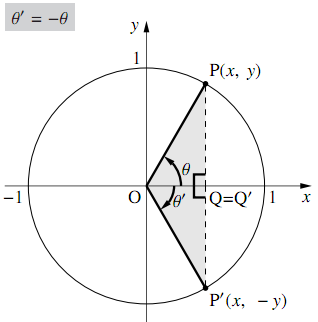
図のように，単位円周上に角$\theta$の動径$\text{OP}$と 角 $-\theta$( $=\theta'$とする)の動径$\text{OP}'$をとる．

点$\text{P}$の座標を$(x,~y)$とすると，$ \triangle{\text{OPQ}}と\triangle{\text{OP}'\text{Q}'}$は合同なので，点$\text{P}'$の座標は$(x,~-y)$となるから

\begin{align} &\sin{\theta'}=-y=\boldsymbol{-\sin\theta}\\ &\cos{\theta'}=x=\boldsymbol{\cos\theta}\\ &\tan{\theta'}=\dfrac{-y}{x}=\boldsymbol{-\tan\theta} \end{align}

$-\theta$の三角比

無題
無題

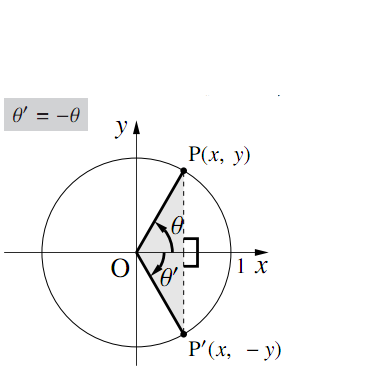
任意の角$\theta$について

\begin{align} &\sin(-\theta)=-\sin\theta\\ &\cos(-\theta)=\cos\theta\\ &\tan(-\theta)=-\tan\theta \end{align}

が成り立つ．

$\theta+\pi$の三角関数

$\theta+\pi$の三角関数

暗記$\theta+\pi$の三角関数

$\sin(\theta+\pi),\cos(\theta+\pi),\tan(\theta+\pi)$を，それぞれ$\sin\theta,\cos\theta,\tan\theta$で表せ．

無題
無題

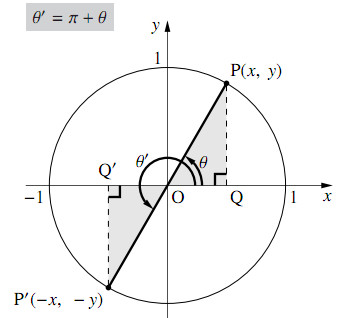
図のように，単位円周上に角$\theta$の動径$\text{OP}$と角$\pi +\theta$( $= \theta'$とする)の動径$\text{OP}'$をとる．

点$\text{P}$の座標を$(x,~y)$とすると， $\triangle{\text{OPQ}}と\triangle{\text{OP}'\text{Q}'}$は合同なので，点$\text{P}'$の座標は$(-x,~-y)$となるから

\begin{align} &\sin{\theta'}=-y=\boldsymbol{-\sin\theta}\\ &\cos{\theta'}=-x=\boldsymbol{-\cos\theta}\\ &\tan{\theta'}=\dfrac{-y}{-x}=\dfrac{y}{x}=\boldsymbol{\tan\theta} \end{align}

$\theta+\pi$の三角比

無題
無題

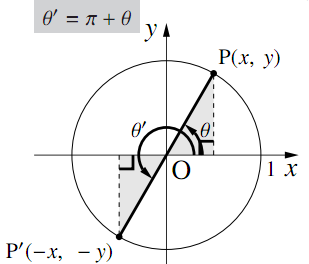
任意の角$\theta$について

\begin{align} &\sin(\theta+\pi)=-\sin\theta\\ &\cos(\theta+\pi)=-\cos\theta\\ &\tan(\theta+\pi)=\tan\theta \end{align}

が成り立つ．

$\theta+\dfrac{\pi}{2}$の三角関数

$\theta+\dfrac{\pi}{2}$の三角関数

暗記$\theta+\dfrac{\pi}{2}$の三角関数

$\sin\left(\theta+\dfrac{\pi}{2}\right),\cos\left(\theta+\dfrac{\pi}{2}\right),\tan\left(\theta+\dfrac{\pi}{2}\right)$を，それぞれ$\sin\theta,\cos\theta,\tan\theta$で表せ．

無題
無題

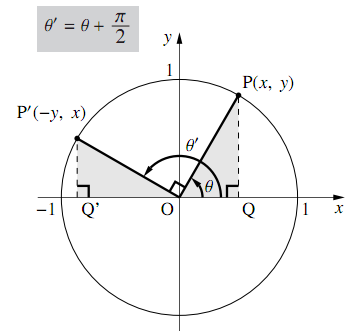
図のように，単位円周上に角$\theta$の動径$\text{OP}$と 角$\theta+\dfrac{\pi}{2}$($ = \theta'$とする)の動径$\text{OP}'$をとる．

点$\text{P}$の座標を$(x,~y)$とすると，$ \triangle{\text{OPQ}}と\triangle{\text{OP}'\text{Q}'}$は合同なので，点$\text{P}'$の座標は$(-y,~x)$となるから

\begin{align} &\sin{\theta'}=x=\boldsymbol{\cos\theta}\\ &\cos{\theta'}=-y=\boldsymbol{-\sin\theta}\\ &\tan{\theta'}=\dfrac{x}{-y}=\boldsymbol{-\dfrac{1}{\tan\theta}} \end{align}

$\theta+\dfrac{\pi}{2}$の三角比

無題
無題

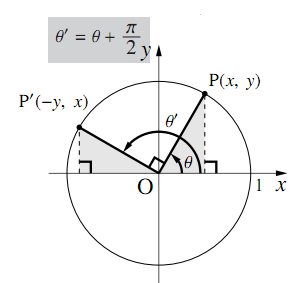
任意の角$\theta$について

\begin{align} &\sin\left(\theta+\dfrac{\pi}{2}\right)=\cos\theta\\ &\cos\left(\theta+\dfrac{\pi}{2}\right)=-\sin\theta\\ &\tan\left(\theta+\dfrac{\pi}{2}\right)=-\dfrac{1}{\tan\theta} \end{align}

が成り立つ．

吹き出し$\theta+\dfrac{\pi}{2}$の三角関数

この節で学んだ公式は丸暗記するようなものではない． 図を書いてすぐに導けるように練習しておこう．