2次関数のグラフ
2次関数の定義
関数 $f(x)$ が \begin{align} &f(x)=2x^2\\ &f(x)=-x^2+12x\\ &f(x)=\dfrac{1}{3}x^2-6x+4 \end{align} のように $x$ の2次式で表されるとき、$f(x)$ は $x$ の2次関数 (quadratic function) であるという。
2次関数の定義
関数 $f(x)$ が $x$ の2次式で表されるとき、つまり、 $a~(\neq0)$、$b$、$c$ を定数として \[f(x)=ax^2+bx+c\] の形で表されるとき、$f(x)$ は $x$ の2次関数 (quadratic function) という。
$y=ax^2$ のグラフ
まずは、2次関数$y=ax^2+bx+c$において$b=c=0$の場合、つまり
\begin{align}
y=ax^2
\end{align}
のグラフについて考えてみよう。
このグラフについては、中学校で学んだように次のような特徴があった。
$y=ax^2$ のグラフの特徴
- 原点を通り、$y$ 軸に関して対称である。
- グラフの $y$ 座標の増減に着目すると
- $\boldsymbol{a\gt0}$ のとき

- $y\geqq0$ の範囲にある。
- $x$ の増加に対し
- $x\lt0$ では $y$ は減少する
- $x\gt0$ では $y$ は増加する
凸 (convex) なグラフという。 - $\boldsymbol{a\lt0}$ のとき
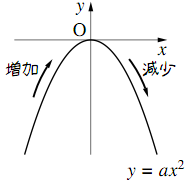
- $y\leqq0$ の範囲にある。
- $x$ の増加に対し
- $x\lt0$ では $y$ は増加する
- $x\gt0$ では $y$ は減少する
放物線の図

一般に、2次関数のグラフにあらわれる曲線のことを
放物線は必ず対称軸をもち、この対称軸のことを単に軸 (axis) といい、この軸と放物線の交点のことを頂点 (vertex) という。
$y=ax^2+c$ のグラフ
次に、$y=ax^2+c$ のグラフについて考えてみよう。これは2次関数 $y=ax^2+bx+c$ において、$b=0$ の場合である。例として2つの2次関数 \[y=2x^2~,~y=2x^2+1\] の関係を考えてみよう。
$2x^2$ と $2x^2+1$ の関係

$y=2x^2+1$のグラフ

上の表から、$y=2x^2+1$ のグラフは、$y=2x^2$ のグラフを $y$ 軸方向に $1$ だけ平行移動した放物線であるとわかる。
この平行移動によって、放物線の軸が $y$ 軸から変わることはない。しかし、頂点は移動し、原点より $y$ 軸方向に $1$ 大きい点 $(0,~1)$ であることがわかる。
$y=x^2+c$ のグラフ
$y=ax^2+c$ のグラフは、$y=ax^2$ のグラフを
「$y$ 軸方向に $c$ だけ平行移動」
した放物線である。このとき、軸は $y$ 軸(直線 $x=0$)、頂点は $(0,~c)$ となる。
$y=a(x-p)^2$ のグラフ
$y=a(x-p)^2$のグラフ

次に $y=a(x-p)^2$ という形をした放物線について考えてみよう。例として、2つの2次関数 \begin{align} &y=2x^2\\ &y=2(x-3)^2 \end{align} の関係を考えてみよう。
この2つの関数について、$x$ を整数としていろいろ変化させてみると、$y$ の値は下の表のようまとめることができる。
| $x$ | $\cdots$ | $-2$ | $-1$ | $0$ | $1$ | $2$ | $3$ | $4$ | $5$ | $\cdots$ |
| $2x^2$ | $\cdots$ | $8$ | $2$ | $0$ | $2$ | $8$ | $18$ | $32$ | $50$ | $\cdots$ |
| $2(x-3)^2$ | $\cdots$ | $50$ | $32$ | $18$ | $8$ | $2$ | $0$ | $2$ | $8$ | $\cdots$ |
この平行移動によって、軸は $x$ 軸方向に $3$ 移動し、直線 $x=3$ に重なる。また、頂点も移動し、原点より $x$ 軸方向に $3$ 大きい点 $(3,~0)$ であることがわかる。
$y=a(x-p)^2$ のグラフ
$y=a(x−p)^2$ のグラフは、$y=ax^2$ のグラフを
「$x$ 軸方向に $p$ だけ平行移動」
した放物線である。このとき、軸は直線 $x=p$、頂点は $(p,~0)$ となる。
放物線を描く~その1~
次の放物線は、$[~~]$内のグラフをどのように平行移動してできたグラフか。また、軸の方程式と頂点の座標を求め、座標平面にグラフで表せ。
- $y=2x^2-3~~[~y=2x^2~]$
- $y=2(x+2)^2~~[~y=2x^2~]$
- $y=-3x^2-1~~[~y=-3x^2~]$
- $y=-3(x-4)^2~~[~y=-3x^2~]$
- $y=2x^2-3$ は $y=2x^2$ のグラフを

$\boldsymbol{y}$ 軸方向に $\boldsymbol{-3}$ 平行移動したグラフ
であるから
軸は $\boldsymbol{y}$ 軸(または直線 $x=0$)、頂点の座標は $\boldsymbol{(0,~-3)}$
である。また、これは下に凸な放物線であるから、グラフは右図のようになる。 - $y=2(x+2)^2$ は $y=2x^2$ のグラフを

$\boldsymbol{x}$ 軸方向に $\boldsymbol{-2}$ 平行移動したグラフ
であるから
軸は $\boldsymbol{x=-2}$、頂点の座標は $\boldsymbol{(-2,~0)}$
である。また、これは下に凸な放物線であるから、グラフは右図のようになる。 - $y=−3x^2−1$ は $y=−3x^2$ のグラフを$\boldsymbol{y}$ 軸方向に $\boldsymbol{−1}$ 平行移動したグラフ

であるから
軸は $\boldsymbol{y}$ 軸(または直線 $x=0$)、頂点の座標は $\boldsymbol{(0,~-1)}$
である。また、これは上に凸な放物線であるから、グラフは右図のようになる。 - $y=−3(x-4)^2$ は $y=-3x^2$ のグラフを

$\boldsymbol{x}$ 軸方向に $\boldsymbol{4}$平行移動したグラフ
であるから
軸は $\boldsymbol{x=4}$、頂点の座標は $\boldsymbol{(4,~0)}$
である。また、これは上に凸な放物線であるから、グラフは右図のようになる。
$y=a(x-p)^2+q$ のグラフ
次に $y=a(x-p)^2+q$ という形をした放物線について考えてみよう。
$y=a(x-p)^2+q$のグラフ

たとえば $y=2(x-3)^2+4$ のグラフについて、右図を見ながら考えてみよう。 \[y=2x^2\] のグラフを $x$ 軸方向に $3$ 平行移動すると \[y=2(x-3)^2\] のグラフになる。さらに、$y$ 軸方向に $4$ 平行移動して \[y=2(x-3)^2+4\] のグラフとなる。
この平行移動によって、軸は原点より $x$ 軸方向に $3$ 大きい、直線 $x=3$ に移動する。
また、頂点も移動し、原点より $x$ 軸方向に $3$ 大きく $y$ 軸方向に $4$ 大きい点 $(3,~4)$ であることがわかる。
$y=a(x-p)^2+q$ のグラフ
$y=a(x−p)^2+q$ のグラフは、$y=ax^2$ のグラフを
「$x$ 軸方向に $p$ だけ平行移動し、$y$ 軸方向に $q$ だけ平行移動」
した放物線である。このとき、軸は直線 $x=p$、頂点は $(p,~q)$ となる。
$y=ax^2+bx+c$ のグラフ
最後に、一般の2次関数 \[y=ax^2+bx+c\] のグラフについて考えてみよう。たとえば \[y=2x^2+4x-1\tag{1}\label{y=ax^2+bx+cnogurafu}\] のグラフを描くには、次のように式を変形(平方完成 (completing square) という)してから考える。 \begin{align} y=&2x^2+4x-1\\ =&2\left\{x^2+2x\right\}-1\\ &\quad\blacktriangleleft x^2の係数でくくる\\ =&2\left\{(x+1)^2-1\right\}-1\\ &\quad\blacktriangleleft 平方の形にする(平方完成)\\ =&2(x+1)^2-2-1\\ &\quad\blacktriangleleft \{~~\}をはずす\\ =&2(x+1)^2-3\\ &\quad\blacktriangleleft 定数項を整理する \end{align} こうすると、既に学んだ『$y=a(x−p)^2+q$ のグラフ』に帰着され、$\eqref{y=ax^2+bx+cnogurafu}$ のグラフは、$y=2x^2$ のグラフを $x$ 軸方向に $-1$、$y$ 軸方向に $-3$ だけ平行移動した放物線になるとわかる。
吹き出し無題
平方完成は慣れないうちは難しく感じるかもしれない。もう一度、ポイントとなるところに焦点をあててみる。 \begin{align} &x^2+\bigcirc{x}\\ =&\left(x+\dfrac{\bigcirc}{2}\right)^2-\left(\dfrac{\bigcirc}{2}\right)^2 \end{align} あとは、$x^2$ の係数に注意しながら、定数項を計算すればよい。
$y=ax^2+bx+c$ のグラフ
$y=ax^2+bx+c$のグラフ

2次関数 $y=ax^2+bx+c$ のグラフは \begin{align} y=&ax^2+bx+c\\ =&a\left\{x^2+\dfrac{b}{a}x\right\}+c\\ &\quad\blacktriangleleft x^2の係数でくくる\\ =&a\left\{\left(x+\frac{b}{2a}\right)^2-\frac{b^2}{4a^2}\right\}+c\\ &\quad\blacktriangleleft 平方完成\\ =&a\left(x+\frac{b}{2a}\right)^2-\frac{b^2}{4a}+c\\ &\quad\blacktriangleleft \{~~\}をはずす\\ =&a\left(x+\frac{b}{2a}\right)^2-\frac{b^2-4ac}{4a}\\ &\quad\blacktriangleleft 定数項を整理する \end{align} と変形することにより、軸が $x=-\dfrac{b}{2a}$ で、頂点が $\left(-\dfrac{b}{2a},~-\dfrac{b^2-4ac}{4a}\right)$ の放物線となることがわかる。
グラフを描くときは、$y$ 軸との交点の $y$ 座標(右のグラフの場合は $c$)を書く習慣をつけよう。これは、$x=0$ のときの $y$ の値である
吹き出し無題
これは暗記するようなものではなく、毎回計算して導き出すものである。
ここまで見たように、2次関数 $y=f(x)=ax^2+bx+c$ のグラフは放物線になる。
そこで、「2次関数 $y=ax^2+bx+c$ のグラフ」のことを「放物線 $y=ax^2+bx+c$」ということがある。
このときの $y=ax^2+bx+c$ は、放物線の方程式 (equation of parabola) といわれる。
放物線を描く~その2~
次の放物線を、頂点の座標を求めてから描け。
- $y=x^2−2x+3$
- $y=−3x^2+6x$
- $y=2x^2+8x+5$
- $y=-2x^2-6x-\dfrac{5}{2}$
- 平方完成すると \begin{align} y=&x^2-2x+3\\ =&(x-1)^2-1+3\\ =&(x-1)^2+2 \end{align} となるから、頂点が $(1,~2)$ で、下に凸な放物線であるから、グラフは右図のようになる。

- 平方完成すると \begin{align} y=&-3x^2+6x\\ =&-3\left\{x^2-2x\right\}\\ =&-3\left\{(x-1)^2-1\right\}\\ =&-3(x-1)^2+3 \end{align} となるから、頂点が $(1,~3)$ で、上に凸な放物線であるから、グラフは右図のようになる。

- 平方完成すると \begin{align} y=&2x^2+8x+5\\ =&2\left\{x^2+4x\right\}+5\\ =&2\left\{(x+2)^2-4\right\}+5\\ =&2(x+2)^2-3 \end{align} となるから、頂点が $(-2,~-3)$ で、下に凸な放物線であるから、グラフは右図のようになる。

- 平方完成すると \begin{align} y=&-2x^2-6x-\dfrac{5}{2}\\ =&-2\left\{x^2+3x\right\}-\dfrac{5}{2}\\ =&-2\left\{\left(x+\dfrac{3}{2}\right)^2-\dfrac{9}{4}\right\}-\dfrac{5}{2}\\ =&-2\left(x+\dfrac{3}{2}\right)^2+2 \end{align} となるから、頂点が $\left(-\dfrac{3}{2},~2\right)$ で、上に凸な放物線であるから、グラフは右図のようになる。
