2次関数とそのグラフ

たとえば、2次関数$f(x)=\dfrac{1}{2}x^2+3x-1$について、$y=f(x)$のグラフを描くには、 $x$の値をいろいろとり、$y=\dfrac{1}{2}x^2+3x-1$を満たす$x$、$y$の値を座標上の点$(x,~y)$として$xy$平面に打っていけばよい。しかし、そのような点は無数にあり、現実的な描き方とはいえない。2次関数のグラフには「頂点」という大きな特徴がある。以下では、この頂点をうまくとらえて2次関数のグラフを描く方法について学んでいこう。

2次関数のグラフ

2次関数の定義

関数 $f(x)$ が \begin{align} &f(x)=2x^2\\ &f(x)=-x^2+12x\\ &f(x)=\dfrac{1}{3}x^2-6x+4 \end{align} のように $x$ の2次式で表されるとき、$f(x)$ は $x$ の2次関数 (quadratic function) であるという。

2次関数の定義

関数 $f(x)$ が $x$ の2次式で表されるとき、つまり、 $a~(\neq0)$、$b$、$c$ を定数として \[f(x)=ax^2+bx+c\] の形で表されるとき、$f(x)$ は $x$ の2次関数 (quadratic function) という。

$y=ax^2$ のグラフ

まずは、2次関数$y=ax^2+bx+c$において$b=c=0$の場合、つまり \begin{align} y=ax^2 \end{align} のグラフについて考えてみよう。
このグラフについては、中学校で学んだように次のような特徴があった。

$y＝ax^2$ のグラフの特徴

  1. 原点を通り、$y$ 軸に関して対称である。
  2. グラフの $y$ 座標の増減に着目すると
    1. 下に凸なグラフ
      $\boldsymbol{a\gt0}$ のとき
      • $y\geqq0$ の範囲にある。
      • $x$ の増加に対し
        • $x\lt0$ では $y$ は減少する
        • $x\gt0$ では $y$ は増加する
      このグラフのようにいったん下がってから上がるグラフのことを、下に凸とつ (convex) なグラフという。
    2. 上に凸なグラフ
      $\boldsymbol{a\lt0}$ のとき
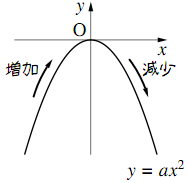
      • $y\leqq0$ の範囲にある。
      • $x$ の増加に対し
        • $x\lt0$ では $y$ は増加する
        • $x\gt0$ では $y$ は減少する
      このグラフのようにいったん上がってから下がるグラフのことを、上に凸 なグラフという。

放物線の図
放物線の図

一般に、2次関数のグラフにあらわれる曲線のことを放物線ほうぶつせん (parabola) という。この名前は、空中に物を放り投げたときにできる軌跡きせきに由来する。

放物線は必ず対称軸をもち、この対称軸のことを単に軸 (axis) といい、この軸と放物線の交点のことを頂点 (vertex) という。

$y=ax^2+c$ のグラフ

次に、$y=ax^2+c$ のグラフについて考えてみよう。これは2次関数 $y=ax^2+bx+c$ において、$b=0$ の場合である。例として2つの2次関数 \[y=2x^2~,~y=2x^2+1\] の関係を考えてみよう。

$2x^2$ と $2x^2+1$ の関係

$2x^2$ と $2x^2+1$ の関係
$y=2x^2+1$のグラフ
$y=2x^2+1$のグラフ

上の表から、$y=2x^2+1$ のグラフは、$y=2x^2$ のグラフを $y$ 軸方向に $1$ だけ平行移動した放物線であるとわかる。

この平行移動によって、放物線の軸が $y$ 軸から変わることはない。しかし、頂点は移動し、原点より $y$ 軸方向に $1$ 大きい点 $(0,~1)$ であることがわかる。

$y＝x^2+c$ のグラフ

$y=ax^2+c$ のグラフは、$y=ax^2$ のグラフを
「$y$ 軸方向に $c$ だけ平行移動」
した放物線である。このとき、軸は $y$ 軸(直線 $x=0$)、頂点は $(0,~c)$ となる。

$y=a(x-p)^2$ のグラフ

$y=a(x-p)^2$のグラフ
$y=a(x-p)^2$のグラフ

次に $y=a(x-p)^2$ という形をした放物線について考えてみよう。例として、2つの2次関数 \begin{align} &y=2x^2\\ &y=2(x-3)^2 \end{align} の関係を考えてみよう。

（注）

この2つの関数について、$x$ を整数としていろいろ変化させてみると、$y$ の値は下の表のようまとめることができる。

$x$$\cdots$$-2$$-1$$0$$1$$2$$3$$4$$5$$\cdots$
$2x^2$$\cdots$$8$$2$$0$$2$$8$$18$$32$$50$$\cdots$
$2(x-3)^2$$\cdots$$50$$32$$18$$8$$2$$0$$2$$8$$\cdots$
上の表から、$y=2(x−3)^2$ のグラフは、$y=2x^2$ のグラフを $x$ 軸方向に $3$ だけ平行移動した放物線であるとわかる。

この平行移動によって、軸は $x$ 軸方向に $3$ 移動し、直線 $x=3$ に重なる。また、頂点も移動し、原点より $x$ 軸方向に $3$ 大きい点 $(3,~0)$ であることがわかる。

$y＝a(x-p)^2$ のグラフ

$y=a(x−p)^2$ のグラフは、$y=ax^2$ のグラフを
「$x$ 軸方向に $p$ だけ平行移動」
した放物線である。このとき、軸は直線 $x=p$、頂点は $(p,~0)$ となる。

放物線を描く～その1～

次の放物線は、$[~~]$内のグラフをどのように平行移動してできたグラフか。また、軸の方程式と頂点の座標を求め、座標平面にグラフで表せ。

  1. $y=2x^2-3~~[~y=2x^2~]$
  2. $y=2(x+2)^2~~[~y=2x^2~]$
  3. $y=-3x^2-1~~[~y=-3x^2~]$
  4. $y=-3(x-4)^2~~[~y=-3x^2~]$

  1. 1の解答
    $y=2x^2-3$ は $y=2x^2$ のグラフを
    $\boldsymbol{y}$ 軸方向に $\boldsymbol{-3}$ 平行移動したグラフ
    であるから
    軸は $\boldsymbol{y}$ 軸（または直線 $x=0$）、頂点の座標は $\boldsymbol{(0,~-3)}$
    である。また、これは下に凸な放物線であるから、グラフは右図のようになる。
  2. 2の解答
    $y=2(x+2)^2$ は $y=2x^2$ のグラフを
    $\boldsymbol{x}$ 軸方向に $\boldsymbol{-2}$ 平行移動したグラフ
    であるから
    軸は $\boldsymbol{x=-2}$、頂点の座標は $\boldsymbol{(-2,~0)}$
    である。また、これは下に凸な放物線であるから、グラフは右図のようになる。
  3. $y=−3x^2−1$ は $y=−3x^2$ のグラフを
    3の解答
    $\boldsymbol{y}$ 軸方向に $\boldsymbol{−1}$ 平行移動したグラフ
    であるから
    軸は $\boldsymbol{y}$ 軸（または直線 $x=0$）、頂点の座標は $\boldsymbol{(0,~-1)}$
    である。また、これは上に凸な放物線であるから、グラフは右図のようになる。
  4. 4の解答
    $y=−3(x-4)^2$ は $y=-3x^2$ のグラフを
    $\boldsymbol{x}$ 軸方向に $\boldsymbol{4}$平行移動したグラフ
    であるから
    軸は $\boldsymbol{x=4}$、頂点の座標は $\boldsymbol{(4,~0)}$
    である。また、これは上に凸な放物線であるから、グラフは右図のようになる。

$y=a(x-p)^2+q$ のグラフ

次に $y=a(x-p)^2+q$ という形をした放物線について考えてみよう。

$y＝a(x-p)^2+q$のグラフ
$y＝a(x-p)^2+q$のグラフ

たとえば $y=2(x-3)^2+4$ のグラフについて、右図を見ながら考えてみよう。 \[y=2x^2\] のグラフを $x$ 軸方向に $3$ 平行移動すると \[y=2(x-3)^2\] のグラフになる。さらに、$y$ 軸方向に $4$ 平行移動して \[y=2(x-3)^2+4\] のグラフとなる。

この平行移動によって、軸は原点より $x$ 軸方向に $3$ 大きい、直線 $x=3$ に移動する。

また、頂点も移動し、原点より $x$ 軸方向に $3$ 大きく $y$ 軸方向に $4$ 大きい点 $(3,~4)$ であることがわかる。

$y＝a(x-p)^2+q$ のグラフ

$y=a(x−p)^2+q$ のグラフは、$y=ax^2$ のグラフを
「$x$ 軸方向に $p$ だけ平行移動し、$y$ 軸方向に $q$ だけ平行移動」
した放物線である。このとき、軸は直線 $x=p$、頂点は $(p,~q)$ となる。

$y=ax^2+bx+c$ のグラフ

最後に、一般の2次関数 \[y=ax^2+bx+c\] のグラフについて考えてみよう。たとえば \[y=2x^2+4x-1\tag{1}\label{y=ax^2+bx+cnogurafu}\] のグラフを描くには、次のように式を変形（平方完成 (completing square) という）してから考える。 \begin{align} y=&2x^2+4x-1\\ =&2\left\{x^2+2x\right\}-1\\ &\quad\blacktriangleleft x^2の係数でくくる\\ =&2\left\{(x+1)^2-1\right\}-1\\ &\quad\blacktriangleleft 平方の形にする（平方完成）\\ =&2(x+1)^2-2-1\\ &\quad\blacktriangleleft \{~~\}をはずす\\ =&2(x+1)^2-3\\ &\quad\blacktriangleleft 定数項を整理する \end{align} こうすると、既に学んだ『$y=a(x−p)^2+q$ のグラフ』に帰着され、$\eqref{y=ax^2+bx+cnogurafu}$ のグラフは、$y=2x^2$ のグラフを $x$ 軸方向に $-1$、$y$ 軸方向に $-3$ だけ平行移動した放物線になるとわかる。

吹き出し無題

平方完成は慣れないうちは難しく感じるかもしれない。もう一度、ポイントとなるところに焦点をあててみる。 \begin{align} &x^2+\bigcirc{x}\\ =&\left(x+\dfrac{\bigcirc}{2}\right)^2-\left(\dfrac{\bigcirc}{2}\right)^2 \end{align} あとは、$x^2$ の係数に注意しながら、定数項を計算すればよい。

$y＝ax^2+bx+c$ のグラフ

$y＝ax^2+bx+c$のグラフ
$y＝ax^2+bx+c$のグラフ

2次関数 $y=ax^2+bx+c$ のグラフは \begin{align} y=&ax^2+bx+c\\ =&a\left\{x^2+\dfrac{b}{a}x\right\}+c\\ &\quad\blacktriangleleft x^2の係数でくくる\\ =&a\left\{\left(x+\frac{b}{2a}\right)^2-\frac{b^2}{4a^2}\right\}+c\\ &\quad\blacktriangleleft 平方完成\\ =&a\left(x+\frac{b}{2a}\right)^2-\frac{b^2}{4a}+c\\ &\quad\blacktriangleleft \{~~\}をはずす\\ =&a\left(x+\frac{b}{2a}\right)^2-\frac{b^2-4ac}{4a}\\ &\quad\blacktriangleleft 定数項を整理する \end{align} と変形することにより、軸が $x=-\dfrac{b}{2a}$ で、頂点が $\left(-\dfrac{b}{2a},~-\dfrac{b^2-4ac}{4a}\right)$ の放物線となることがわかる。

グラフを描くときは、$y$ 軸との交点の $y$ 座標（右のグラフの場合は $c$）を書く習慣をつけよう。これは、$x=0$ のときの $y$ の値である

吹き出し無題

これは暗記するようなものではなく、毎回計算して導き出すものである。

ここまで見たように、2次関数 $y=f(x)=ax^2+bx+c$ のグラフは放物線になる。

そこで、「2次関数 $y=ax^2+bx+c$ のグラフ」のことを「放物線 $y=ax^2+bx+c$」ということがある。

このときの $y=ax^2+bx+c$ は、放物線の方程式 (equation of parabola) といわれる。

放物線を描く～その２～

次の放物線を、頂点の座標を求めてから描け。

  1. $y=x^2−2x+3$
  2. $y=−3x^2+6x$
  3. $y=2x^2+8x+5$
  4. $y=-2x^2-6x-\dfrac{5}{2}$

  1. $y=x^2−2x+3$
    平方完成すると \begin{align} y=&x^2-2x+3\\ =&(x-1)^2-1+3\\ =&(x-1)^2+2 \end{align} となるから、頂点が $(1,~2)$ で、下に凸な放物線であるから、グラフは右図のようになる。
  2. $y=−3x^2+6x$
    平方完成すると \begin{align} y=&-3x^2+6x\\ =&-3\left\{x^2-2x\right\}\\ =&-3\left\{(x-1)^2-1\right\}\\ =&-3(x-1)^2+3 \end{align} となるから、頂点が $(1,~3)$ で、上に凸な放物線であるから、グラフは右図のようになる。
  3. $y=2x^2+8x+5$
    平方完成すると \begin{align} y=&2x^2+8x+5\\ =&2\left\{x^2+4x\right\}+5\\ =&2\left\{(x+2)^2-4\right\}+5\\ =&2(x+2)^2-3 \end{align} となるから、頂点が $(-2,~-3)$ で、下に凸な放物線であるから、グラフは右図のようになる。
  4. $y=-2x^2-6x-\dfrac{5}{2}$
    平方完成すると \begin{align} y=&-2x^2-6x-\dfrac{5}{2}\\ =&-2\left\{x^2+3x\right\}-\dfrac{5}{2}\\ =&-2\left\{\left(x+\dfrac{3}{2}\right)^2-\dfrac{9}{4}\right\}-\dfrac{5}{2}\\ =&-2\left(x+\dfrac{3}{2}\right)^2+2 \end{align} となるから、頂点が $\left(-\dfrac{3}{2},~2\right)$ で、上に凸な放物線であるから、グラフは右図のようになる。

グラフの移動

2次関数の平行移動

ここでは、2次関数のグラフの平行移動について考える。

2次関数グラフの平行移動〜その1〜

$f(x)=\dfrac{1}{2}x^2-x+\dfrac{3}{2}$ とし、放物線 $y=f(x)$ を $C$ とよぶ。

  1. $C$ を $x$ 軸方向に $2$ 平行移動したグラフ $C_1$ の式を求めよ。
  2. $C$ を $y$ 軸方向に $1$ 平行移動したグラフ $C_2$ の式を求めよ。

1、2のグラフ
1、2のグラフ

平方完成をすると、$f(x)=\dfrac{1}{2}(x-1)^2+1$ となるので、頂点の座標は $(1,~1)$ とわかる。

  1. 頂点が $(3,~1)$ となればよいので \begin{align} &y=\dfrac{1}{2}(x-3)^2+1\\ \Leftrightarrow~&\boldsymbol{y=\dfrac{1}{2}x^2-3x+\dfrac{11}{2}} \end{align}
  2. 頂点が $(1,~2)$ となればよいので \begin{align} &y=\dfrac{1}{2}(x-1)^2+2\\ \Leftrightarrow~&\boldsymbol{y=\dfrac{1}{2}x^2-x+\dfrac{5}{2}} \end{align}

上の例題を別の見方でとらえてみよう。

たとえば、$C_1$ 上の各点 $P(x,~y)$ において、問題とは逆向きに $x$ 軸方向に $-2$ 平行移動した点 $Q(x-2,~y)$ は $C$ 上の点だから \begin{align} &y=\dfrac{1}{2}(x-2)^2-(x-2)+\dfrac{3}{2}\\ \Leftrightarrow~&\boldsymbol{y=\dfrac{1}{2}x^2-3x+\dfrac{11}{2}} \end{align} として答えを求めることができる。

このようなやり方は、$y$ 軸方向への平行移動でも実行できる。上の例題の2で各自それを確かめてみよ。

放物線の平行移動

放物線 $y=ax^2+bx+c$ を $x$ 軸に $p$、$y$ 軸に $q$ だけ平行移動した放物線の方程式は、$x$ を $x-p$、$y$ を $y-q$ におきかえると \begin{align} &y-q=a(x-p)^2+b(x-p)+c\\ \Leftrightarrow~&y=a(x-p)^2+b(x-p)+c+q \end{align} となる。

2次関数グラフの平行移動〜その2〜

放物線 $y=x^2-x+1$ を、$x$ 軸方向に $1$、$y$ 軸方向に $2$ だけ平行移動して得られる放物線の方程式を求めよ。

$x$ を $x-1$、$y$ を $y-2$ におきかえて \begin{align} &y-2=(x-1)^2-(x-1)+1\\ \Leftrightarrow~&\boldsymbol{y=x^2-3x+5} \end{align}

2次関数の対称移動

次に、2次関数のグラフの対称移動について考える。

2次関数グラフの対称移動〜その1〜

$f(x)=\dfrac{1}{2}x^2-x+\dfrac{3}{2}$ とし、放物線 $y=f(x)$ を $C$ とよぶ。

  1. $C$ を $x$ 軸に関して対称移動したグラフ $C_x$ の式を求めよ。
  2. $C$ を $y$ 軸に関して対称移動したグラフ $C_y$ の式を求めよ。
  3. $C$ を原点に関して対称移動したグラフ $C_{xy}$ の式を求めよ。

1,2,3のグラフ
1,2,3のグラフ

平方完成をすると、$f(x)=\dfrac{1}{2}(x-1)^2+1$ となるので、頂点の座標は $(1,~1)$ とわかる。

  1. 頂点が $(1,~-1)$ となり、上に凸なグラフになればよいので \begin{align} &y=-\dfrac{1}{2}(x-1)^2-1\\ \Leftrightarrow~&\boldsymbol{y=-\dfrac{1}{2}x^2+x-\dfrac{3}{2}} \end{align}
  2. 頂点が $(-1,~1)$ となればよいので \begin{align} &y=\dfrac{1}{2}(x+1)^2+1\\ \Leftrightarrow~&\boldsymbol{y=\dfrac{1}{2}x^2+x+\dfrac{3}{2}} \end{align}
  3. 頂点が $(-1,~-1)$ となり、上に凸なグラフになればよいので \begin{align} &y=-\dfrac{1}{2}(x+1)^2-1\\ \Leftrightarrow~&\boldsymbol{y=-\dfrac{1}{2}x^2-x-\dfrac{3}{2}} \end{align}

上の例題を別の見方でとらえてみよう。

$y=-\dfrac{1}{2}x^2+x-\dfrac{3}{2}$
$y=-\dfrac{1}{2}x^2+x-\dfrac{3}{2}$

たとえば、$C_x$ 上の各点 $P(x,~y)$ において、問題とは逆に $x$ 軸に関して対称移動した点 $Q(x,~-y)$ は $C$ 上の点だから \begin{align} &-y=\dfrac{1}{2}x^2-x+\dfrac{3}{2}\\ \Leftrightarrow~&\boldsymbol{y=-\dfrac{1}{2}x^2+x-\dfrac{3}{2}} \end{align} として答えを求めることができる。

このようなやり方は、$y$ 軸に関する対称移動でも実行できる。上の例題の2と3で各自それを確かめてみよ。

放物線の対称移動

放物線 $y=ax^2+bx+c$ を $x$ 軸に関して対称移動した放物線の方程式は、$y$ を $-y$ におきかえた \begin{align} -y&=ax^2+bx+c\\ {\Leftrightarrow}y&=-ax^2-bx-c \end{align} また、$y$ 軸に関して対称移動した放物線の方程式は、$x$ を $-x$ におきかえた \begin{align} y&=a(-x)^2+b(-x)+c\\ {\Leftrightarrow}y&=ax^2-bx+c \end{align} また、原点に関して対称移動した放物線の方程式は、$y$ を $-y$ に、$x$ を $-x$ におきかえた \begin{align} -y&=a(-x)^2+b(-x)+c\\ {\Leftrightarrow}y&=-ax^2+bx-c \end{align} となる。

吹き出し無題

原点に関する対称移動は、上の例題の図からもわかるように、$x$ 軸に関する対象移動と $y$ 軸に関する対称移動をあわせたものとして理解できる。

2次関数グラフの対称移動〜その2〜

放物線 $y=x^2+4x-5$ を、次の直線または点に関して、それぞれ対称移動して得られる放物線の方程式を求めよ。

  1. $x$ 軸
  2. $y$ 軸
  3. 原点

  1. $y$ を $-y$ におきかえて \begin{align} -&y=x^2+4x-5\\ \Leftrightarrow~&\boldsymbol{y=-x^2-4x+5} \end{align}
  2. $x$ を $-x$ におきかえて \begin{align} &y=(-x)^2+4(-x)-5\\ \Leftrightarrow~&\boldsymbol{y=x^2-4x-5} \end{align}
  3. $x$ を $-x$ に、$y$ を $-y$ におきかえて \begin{align} -&y=(-x)^2+4(-x)-5\\ \Leftrightarrow~&\boldsymbol{y=-x^2+4x+5} \end{align}

一般のグラフの平行移動と対称移動については、『グラフの移動について』を参照のこと。

2次関数の決定

軸や頂点に関する条件が与えられた場合

この場合には、『$y=a(x-p)^2+q$ のグラフ』で学んだことを使って問題を解くとよい。

頂点や軸に関する条件が与えられた場合

グラフが次の条件を満たす2次関数を求めよ。

  1. 頂点が $(1,~-3)$ で、点 $(-1,~5)$ を通る。
  2. 軸が直線 $x=-2$ で、2点 $(-3,~2)$、$(0,~-1)$ を通る。

  1. グラフの頂点が $(1,~-3)$ であるから、求める2次関数は \[y=a(x-1)^2-3\] と表せる。さらに、このグラフは点 $(-1,~5)$ を通るから、$x=-1$ のとき $y=5$ となる。したがって \begin{align} &5=a(-1-1)^2-3\\ \Leftrightarrow~&5=4a-3\\ \therefore~&a=2 \end{align} よって、求める2次関数は $y=2(x-1)^2-3$、つまり \[\boldsymbol{y=2x^2-4x-1}\]

  2. 軸が直線 $x=-2$ であるから、求める2次関数は \[y=a(x+2)^2+q\] と表せる。さらに、このグラフは2点 $(-3,~2)$、$(0,~-1)$ を通るから \begin{align} &\begin{cases} 2=a(-3+2)^2+q\\ -1=a(0+2)^2+q \end{cases}\\ \Leftrightarrow~~~ &\begin{cases} 2=a+q\\ -1=4a+q \end{cases} \end{align} この連立方程式を解いて、$a=-1$、$q=3$ を得る。

    よって、求める2次関数は $y=-(x+2)^2+3$、つまり \[\boldsymbol{y=-x^2-4x-1}\]

グラフ上の3点が与えられた場合

この場合は、求める2次関数を $y=ax^2+bx+c$ とおいて考えるとよい。

グラフ上の3点が与えられた場合

グラフが3点 $A(1,~6)$、$B(-2,~-9)$、$C(4,~3)$ を通るような2次関数を求めよ。

求める2次関数を \[y=ax^2+bx+c\] とおく。このグラフは、3点 $A$、$B$、$C$ を通るから \begin{align} &\begin{cases} ~6=a\cdot1^2+b\cdot1+c\\ -9=a\cdot(-2)^2+b\cdot(-2)+c\\ ~3=a\cdot4^2+b\cdot4+c\\ \end{cases}\\ \Leftrightarrow &\begin{cases} ~6=a+b+c~\cdots(1)\\ -9=4a-2b+c~\cdots(2)\\ ~3=16a+4b+c~\cdots(3) \end{cases} \end{align} を得る。以下、3つの文字を含むこの連立方程式を解く。 まず、$(2)-(1)$ より、$3a-3b=-15$、よって \[a-b=-5~~~{\cdots}(4)\] さらに、$(3)-(2)$ より、$12a+6b=12$、よって \[2a+b=2~~~{\cdots}(5)\] $(4)$、$(5)$ の連立方程式を解いて $a=-1$、$b=4$。さらに、これらを $(1)$ に代入して $c=3$ を得る。 よって、求める2次関数は \[\boldsymbol{y=-x^2+4x+3}\]

吹き出し無題

2次関数の決定にあたっては、未知の2次関数を

  • $y=a(x-p)^2+q$
  • $y=ax^2+bx+c$
  • $y=a(x-\alpha)(x-\beta)$
のうち、どの形で表現するかが重要である。2次関数の $y=a(x-\alpha)(x-\beta)$ の形については、『2次関数から2次方程式を考える』において学ぶ。

2次関数の最大・最小

2次関数の最大・最小

ここでは、グラフを利用して2次関数の最大値や最小値を求める方法を考えよう。

$y=x^2-4x+5$
$y=x^2-4x+5$

たとえば、$f(x)=x^2-4x+5$ は \[f(x)=x^2-4x+5=(x-2)^2+1\] と変形できるので、$y=f(x)$ のグラフは点 $(2,~1)$ を頂点とする下に凸な放物線であることがわかり、グラフは右図のようになる。このグラフは、$x$ の増加に対し
「$x\lt2$ の範囲では $y$ の値が減少、$2\lt{x}$ の範囲では $y$ の値は増加」
する。そのため、$y$ の値が減少から増加に転じる $x=2$ で、最小値 $1$ をとる。また、$y$ の値はいくらでも大きくなるので、最大値は存在しない。

$y=-\dfrac{1}{2}x^2-2x+1$
$y=-\dfrac{1}{2}x^2-2x+1$

また、$g(x)=-\dfrac{1}{2}x^2-2x+1$ は \[g(x)=-\dfrac{1}{2}x^2-2x+1=-\dfrac{1}{2}(x+2)^2+3\] と変形できるので、$y=g(x)$ のグラフは点 $(-2,~3)$ を頂点とする上に凸な放物線であることがわかり、グラフは右図のようになる。このグラフは、$x$ の増加に対し
「$x\lt-2$ の範囲では $y$ の値が増加、$-2\lt{x}$ の範囲では $y$ の値は減少」
する。そのため、$y$ の値が増加から減少に転じる $x=-2$ で、最大値 $3$ をとる。また、$y$ の値はいくらでも小さくなるので、最小値は存在しない。

  1. $a\gt0$ の場合
    $a\gt0$ の場合
  2. $a\lt0$ の場合
    $a\lt0$ の場合

定義域が限定された2次関数の最大・最小

2次関数の最大・最小〜その1〜

2次関数 $f(x)=x^2-2x-2$ において、定義域を次の1～5としたときの、最大値・最小値をそれぞれ求めよ。

  1. $-2\leqq{x}\leqq0$
  2. $-1\leqq{x}\leqq2$
  3. $0\leqq{x}\leqq2$
  4. $0\leqq{x}\leqq3$
  5. $3\leqq{x}\leqq4$

平方完成によって $f(x)=(x-1)^2-3$ と変形できる。

そこで $y=(x-1)^2-3$ のグラフを、与えられた定義域内で描いて考える。

  1. 1のグラフ
    定義域が $-2\leqq{x}\leqq0$ の場合、$y=f(x)$ のグラフは右図の実線部分となるので
    • 最大値 $f(-2)=\boldsymbol{6}$
    • 最小値 $f(0)=\boldsymbol{-2}$
    となる。
    $\blacktriangleleft$ 放物線は下に凸、頂点は定義域内になく、$y$ の値は定義域内で常に減少している。その結果 $y$ 座標が最も大きいのは定義域の左端であり、$y$ 座標が最も小さいのは定義域の右端である。
  2. 2のグラフ
    定義域が $-1\leqq{x}\leqq2$ の場合、$y=f(x)$ のグラフは右図の実線部分となるので
    • 最大値 $f(-1)=\boldsymbol{1}$
    • 最小値 $f(1)=\boldsymbol{-3}$
    となる。
    $\blacktriangleleft$ 頂点は定義域内の右半分にある。その結果 $y$ 座標が最も大きいのは定義域の左端であり、$y$ 座標が最も小さいのは放物線の頂点である。
  3. 3のグラフ
    定義域が $0\leqq{x}\leqq2$ の場合、$y=f(x)$ のグラフは右図の実線部分となるので
    • 最大値 $f(2)=f(0)=\boldsymbol{-2}$
    • 最小値 $f(1)=\boldsymbol{-3}$
    となる。
    $\blacktriangleleft$ 頂点は定義域内のまん中にある。その結果 $y$ 座標が最も大きいのは定義域の両端であり、$y$ 座標が最も小さいのは放物線の頂点である。
  4. 4のグラフ
    定義域が $0\leqq{x}\leqq3$ の場合、$y=f(x)$ のグラフは右図の実線部分となるので
    • 最大値 $f(3)=\boldsymbol{1}$
    • 最小値 $f(1)=\boldsymbol{-3}$
    となる。
    $\blacktriangleleft$ 頂点は定義域内の左半分にある。その結果 $y$ 座標が最も大きいのは定義域の右端であり、$y$ 座標が最も小さいのは放物線の頂点である。
  5. 5のグラフ
    定義域が $3\leqq{x}\leqq4$ の場合、$y=f(x)$ のグラフは右図の実線部分となるので
    • 最大値 $f(4)=\boldsymbol{6}$
    • 最小値 $f(3)=\boldsymbol{1}$
    となる。
    $\blacktriangleleft$ 頂点は定義域内になく、$y$ の値は定義域内で常に増加している。その結果 $y$ 座標が最も大きいのは定義域の右端であり、$y$ 座標が最も小さいのは定義域の左端である。

2次関数の最大・最小〜その2〜

1～4の全ての2次関数について定義域が $-1\leqq{x}\leqq2$ であるとき、最大値・最小値をそれぞれ求めよ。

  1. $f(x)=x^2+4x-3$
  2. $f(x)=-x^2-x-2$
  3. $f(x)=\dfrac{1}{2}x^2-x-3$
  4. $f(x)=-3x^2+12x-5$

  1. 1のグラフ
    $f(x)$ を平方完成すると \[f(x)=(x+2)^2-7\] 定義域が $-1\leqq{x}\leqq2$ の場合、$y=f(x)$ のグラフは右図の実線部分となるので
    • 最大値 $f(2)=\boldsymbol{9}$
    • 最小値 $f(-1)=\boldsymbol{-6}$
    となる。
    $\blacktriangleleft$ 放物線は下に凸、頂点は定義域内になく、$y$ の値は定義域内で常に増加している。その結果 $y$ 座標が最も大きいのは定義域の右端であり、$y$ 座標が最も小さいのは定義域の左端である。
  2. 2のグラフ
    $f(x)$ を平方完成すると \[f(x)=-\left(x+\dfrac{1}{2}\right)^2-\dfrac{7}{4}\] 定義域が $-1\leqq{x}\leqq2$ の場合、$y=f(x)$ のグラフは右図の実線部分となるので
    • 最大値 $f\left(-\dfrac{1}{2}\right)=\boldsymbol{-\dfrac{7}{4}}$
    • 最小値 $f(2)=\boldsymbol{-8}$
    となる。
    $\blacktriangleleft$ 放物線は上に凸、頂点は定義域内の左半分にある。その結果 $y$ 座標が最も大きいのは放物線の頂点であり、$y$ 座標が最も小さいのは定義域の右端である。
  3. 3のグラフ
    $f(x)$ を平方完成すると \[f(x)=\dfrac{1}{2}(x-1)^2-\dfrac{7}{2}\] 定義域が $-1\leqq{x}\leqq2$ の場合、$y=f(x)$ のグラフは右図の実線部分となるので
    • 最大値 $f(-1)=\boldsymbol{-\dfrac{3}{2}}$
    • 最小値 $f(1)=\boldsymbol{-\dfrac{7}{2}}$
    となる。
    $\blacktriangleleft$ 放物線は下に凸、頂点は定義域内の右半分にある。その結果 $y$ 座標が最も大きいのは定義域の左端であり、$y$ 座標が最も小さいのは放物線の頂点である。
  4. 4のグラフ
    $f(x)$ を平方完成すると \[f(x)=-3(x-2)2+7\] 定義域が $-1\leqq{x}\leqq2$ の場合、$y=f(x)$ のグラフは右図の実線部分となるので
    • 最大値 $f(2)=\boldsymbol{7}$
    • 最小値 $f(-1)=\boldsymbol{-20}$
    となる。
    $\blacktriangleleft$ 放物線は上に凸、頂点は定義域の右端にあり、$y$ の値は定義域内で常に増加している。その結果 $y$ 座標が最も大きいのは定義域の右端であり、$y$ 座標が最も小さいのは定義域の左端である。

吹き出し無題

定義域が限定された放物線は、最大値・最小値を与えるグラフ上の点に着目すれば、以下の5種類にまとめられる（$y$ 座標が最大になる点を $\blacktriangle$、最小になる点を $\bullet$ で表している）。

放物線の最大値と最小値の図
放物線の最大値と最小値の図

文字定数を含む2次関数の最大・最小

文字定数を含む2次関数の形の判別

放物線 \[C:y=x^2-4ax+a^2~~(-5\leqq{x}\leqq5)\] について以下の問に答えよ。

  1. $C$ の軸が定義域より左側にあるための、$a$ の範囲を求めよ。また、定義域内における $C$ の最大値、最小値を求めよ。
  2. $C$ の軸が定義域より右側にあるための、$a$ の範囲を求めよ。また、定義域内における $C$ の最大値、最小値を求めよ。
  3. $C$ の軸が定義域の中にあるための、$a$ の範囲を求めよ。また、この範囲のうち、定義域の左端で $C$ が最大となるような $a$ の範囲を求め、このときの $C$ の最大値、最小値を求めよ。

$y=x^2-4ax+a^2$ の右辺を平方完成すると \[y=(x-2a)^2-3a^2\] となるので、このグラフの軸は $x=2a$ である。

  1. 1のグラフ
    放物線の軸 $x=2a$ が定義域の左端 $x=-5$ よりさらに左にあればよい。よって \[2a\lt-5~\Leftrightarrow~\boldsymbol{a\lt-\dfrac{5}{2}}\]
    • $y$ 座標が最大となるのは定義域の右端なので、最大値 $\boldsymbol{a^2-20a+25}$（$x=5$ のとき）
    • $y$ 座標が最小となるのは定義域の左端なので、最小値 $\boldsymbol{a^2+20a+25}$（$x=-5$ のとき）
  2. 2のグラフ
    放物線の軸 $x=2a$ が定義域の右端 $x=5$ よりさらに右にあればよい。 \[5\lt2a~\Leftrightarrow~\boldsymbol{\dfrac{5}{2}\lt{a}}\]
    • $y$ 座標が最大となるのは定義域の左端なので、最大値 $\boldsymbol{a^2+20a+25}$（$x=-5$ のとき）
    • $y$ 座標が最小となるのは定義域の右端なので、最小値 $\boldsymbol{a^2-20a+25}$（$x=5$ のとき）
  3. 3のグラフ
    放物線の軸 $x=2a$ が定義域の中にあるためには \[-5\leqq2a\leqq5~\Leftrightarrow~\boldsymbol{-\dfrac{5}{2}\leqq{a}\leqq\dfrac{5}{2}}\] さらに、定義域の左端で $y$ 座標が最大となるには、軸が定義域の右半分に存在すればよい。つまり \[0\leqq2a\leqq5~\Leftrightarrow~\boldsymbol{0\leqq{a}\leqq\dfrac{5}{2}}\]
    • $y$ 座標が最大となるのは定義域の左端なので、最大値 $\boldsymbol{a^2+20a+25}$（$x=-5$ のとき）
    • $y$ 座標が最小となるのは $C$ の頂点なので、最小値 $\boldsymbol{-3a^2}$（$x=2a$ のとき）

吹き出し無題

上の問題において、$a=0$ のときは定義域の両端で最大値をとる。

2次関数の最大・最小（文字定数を含む場合）

2次関数 \[f(x)=x^2-4x+5~(0\leqq{x}\leqq{a})\] について以下の問に答えよ。ただし、$a\gt0$ とする。

  1. 最小値を求めよ。
  2. 最大値を求めよ。

$y=f(x)$ を平方完成して \[y=(x-2)^2+1\] となるので、このグラフをもとに問に答える。

    1. 1-iの図
      $\boldsymbol{0\lt{a}\lt2}$ のとき $0\leqq{x}\leqq{a}$ におけるこの関数のグラフは、右図の放物線の実線部分となる。この定義域内では、関数の値は減少するから、最小値は $f(a)=a^2-4a+5$ となる。
    2. 1-iiの図
      $\boldsymbol{2\leqq{a}}$ のとき $0\leqq{x}\leqq{a}$ におけるこの関数のグラフは、右図の放物線の実線部分となる。この場合には、定義域内に軸 $x=2$ が含まれるから、最小値は $f(2)=1$ となる。
    以上i、iiをまとめると
    • $\boldsymbol{0\lt{a}\lt2}$ のとき、最小値 $f(a)=\boldsymbol{a^2-4a+5}$
    • $\boldsymbol{2\leqq{a}}$ のとき、最小値 $f(2)=\boldsymbol{1}$
    1. 2-iの図
      $\boldsymbol{0\lt{a}\lt4}$ のとき $0\leqq{x}\leqq{a}$ におけるこの関数のグラフは、右図の放物線の実線部分となる。この場合には、定義域の両端の $y$ 座標を比べると、左端の方が大きい。よって、最大値は $f(0)=5$ となる。
    2. 2-iiの図
      $\boldsymbol{4\leqq{a}}$ のとき $0\leqq{x}\leqq{a}$ におけるこの関数のグラフは、右図の放物線の実線部分となる。この場合には、定義域の両端の $y$ 座標を比べると、右端の方が大きい。よって、最大値は $f(a)=a^2-4a+5$ となる。
    以上i、iiをまとめると
    • $\boldsymbol{0\lt{a}\lt4}$ のとき、最大値 $f(0)=\boldsymbol{5}$
    • $\boldsymbol{4\leqq{a}}$ のとき、最大値 $f(a)=\boldsymbol{a^2-4a+5}$

吹き出し無題

$a$ の値を $0$ から増やしていくとき、グラフの最大値・最小値をとる点がいつ変わるのかグラフを描いて考えて、場合分けをしよう。

2次関数の最大・最小の応用

2次関数の知識を利用して、現実にあるさまざまな問題を解くことができる。

2次関数の応用

  1. 長さ $20\text{cm}$ の針金を2つに切り、それぞれの針金で正方形を作るとき、それらの面積の和の最小値を求めよ。また、そのとき針金は何 $\text{cm}$ ずつに切り分けられているか求めよ。
  2. ある品物の売価が1個 $120$ 円のときには、1日の売上個数は $400$ 個であるという。売価を1個につき1円値上げするごとに、1日の売上個数は $2$ 個ずつ減るという。1日の売上金額を最大にするには、売価をいくらに設定すればよいか求めよ。

  1. $20\text{cm}$ の針金を、$4x\text{cm}$ と $(20-4x)\text{cm}$ に切り分けたとする。ただし、$0\lt{x}\lt5$ とする。

    それぞれの針金から作られる正方形の面積は \begin{align} &\dfrac{4x}{4}\times\dfrac{4x}{4}=x\times{x}\\ &\dfrac{20-4x}{4}\times\dfrac{20-4x}{4}=(5-x)\times(5-x) \end{align} となるから、これら2つの正方形の面積の和を $f(x)(\text{cm}^2)$ とすると \begin{align} f(x)=&x^2+(5-x)^2\\ =&x^2+25-10x+x^2\\ =&2x^2-10x+25 \end{align} となる。ここで、$f(x)$ は \begin{align} f(x)=&2\left\{\left(x-\dfrac{5}{2}\right)^2-\dfrac{25}{4}\right\}+25\\ =&2\left(x-\dfrac{5}{2}\right)^2+\dfrac{25}{2} \end{align}

    1のグラフ
    と変形できるから、$y=f(x)$ のグラフは $0\lt{x}\lt5$ で右図のようになる。

    これより最小値は $f\left(\dfrac{5}{2}\right)$ であるから、面積の和の最小値は $\boldsymbol{\dfrac{25}{2}{\text{cm}}^2}$ であり、$x=10$ のとき最小値となるのだから、針金は $\boldsymbol{10\text{cm}}$ずつに切り分けられる。

  2. 売価を1個 $x$ 円（$120\leqq{x}\leqq320$）とすると、$120$ 円より $(x-120)$ 円値上げしたことになる。その結果、1日の売上個数は、$2(x-120)$ 個減る。

    よって、1日の売上金額 $f(x)$ は \begin{align} f(x)=&x\left\{400-2(x-120)\right\}\\ =&x(640-2x)\\ =&-2x^2+640x \end{align} となる。ここで、$f(x)$ は \begin{align} f(x)=&-2(x^2-320x)\\ =&-2\left\{(x-160)^2-25600\right\}\\ =&-2(x-160)^2+51200 \end{align}

    2のグラフ
    と変形できるから、$y=f(x)$ のグラフは $120\leqq{x}\leqq{320}$ で右図のようになる。

    これより、最大値は $f(160)$ をとるには、$x=160$。つまり、売価を $\boldsymbol{160}$ 円にすればよい。

条件をもつ2次関数の最大・最小

$0{\leqq}x$、$0{\leqq}y$、$2x+y=10$ のとき、$x^2+y^2−3$ の最大値・最小値と、そのときの $x$、$y$ を求めよ。

1のグラフ
1のグラフ

$2x+y=10$ を $y$ について解けば $y=10−2x$。これを $0{\leqq}y$ に代入すれば \begin{align} 0{\leqq}y\Leftrightarrow~&0{\leqq}10-2x\\ \Leftrightarrow~&x\leqq5 \end{align} であり、さらに、$x^2+y^2-3$ に代入すれば \begin{align} x^2+y^2-3&=x^2+(10-2x)^2-3\\ &=5x^2-40x+97 \end{align} である。つまり、$0{\leqq}x\leqq5$ のときに、2次関数 \[5x^2-40x+97\] の最大・最小を求めればよい。この2次関数を $f(x)$ とおいて平方完成すると \[f(x)=5(x-4)^2+17\] そこでグラフ $L=f(x)~(0{\leqq}x\leqq5)$ を描けば、右図のようになり、$f(x)$ の最大値は $f(0)=97$、最小値は $f(4)=17$ とわかる。

$x=0$ のとき $y=10$、$x=4$ のとき $y=2$ であるから、答えは次のようになる。

  • $\boldsymbol{(x,~y)=(0,~10)}$ のとき最大値 $\boldsymbol{97}$
  • $\boldsymbol{(x,~y)=(4,~2)}$ のとき最小値 $\boldsymbol{17}$

式の一部を文字でおく

関数 $y=(x^2-2x)^2+4x^2-8x+5$ について以下の問に答えよ。

  1. $t=x^2-2x$ とするとき、$t$ の値のとりうる範囲を求めよ。
  2. $y$ の値のとりうる範囲を求めよ。

  1. 1のグラフ
    平方完成によって \[t=(x-1)^2-1\] であるので、右図より $\boldsymbol{t\geqq-1}$。
  2. $y$ を $t$ で表し平方完成すれば \begin{align} y&=(x^2-2x)^2+4(x^2-2x)+5\\ &=t^2+4t+5\\ &=(t+2)^2+1 \end{align}
    2のグラフ
    となる。1より $-1\leqq{t}$ であるので、$t$ に対する $y$ のグラフは右図のようになる。つまり、$\boldsymbol{y\geqq2}$。

放物線と$x$軸の位置関係-判別式D

放物線と$x$軸の位置関係-判別式D

放物線と $x$ 軸との位置関係については、次の3つのパターンに分けられる。ただし、グラフは下に凸な場合のものである。

  1. $x$ 軸と2つの共有点をもつ
    iの図
  2. $x$ 軸と1つの共有点をもつ
    iiの図
  3. $x$ 軸と共有点をもたない
    iiiの図

$y=2(x+2)^2-7$
$y=2(x+2)^2-7$

たとえば、放物線 $y=2x^2+8x+1$ は平方完成によって \begin{align} y=&2x^2+8x+1\\ =&2\{x^2+4x\}+1\\ =&2\left\{\left(x+2\right)^2-4\right\}+1\\ =&2(x+2)^2-7 \end{align} となり、頂点の座標は $(-2,~-7)$ とわかる。特に、頂点の $y$ 座標は負であるから、グラフは右上図のようになり、上のパターンiであることがわかる。

このように、2次関数が与えられたとき、頂点の $y$ 座標の符号を調べれば、グラフがこの3つのパターンのうちどれに属するかを知ることができる。

では、一般の放物線 $y=ax^2+bx+c~(a\neq0)$ について考えてみよう。『$y=ax^2+bx+c$ のグラフ』で学んだように、平方完成は \[y=ax^2+bx+c=a\left(x+\dfrac{b}{2a}\right)^2-\dfrac{b^2-4ac}{4a}\] となる。そして $a\gt0$ の場合は、この頂点の $y$ 座標の値 $-\dfrac{b^2-4ac}{4a}$ の負・$0$・正が上のパターンi・ii・iiiと対応している。

（注）

$-\dfrac{b^2-4ac}{4a}$ の符号は、分子の $b^2-4ac$ と分母にある $a$ の符号がわかれば確定する。($a$ の正負は、グラフが下に凸か上に凸かを決めているだけなので、$b^2-4ac$ の符号を調べれば2次関数と $x$ 軸との位置関係を判別できる。)そこで、分子に表れる $b^2-4ac$ という式を判別式 (discriminant) とよび、$D$ であらわす。

判別式 $D$ の定義

2次関数 $y=ax^2+bx+c$ において、$b^2-4ac$ を判別式 $D$ とよぶ。つまり \[D=b^2-4ac\] とする。

いま、この判別式 $D$ の符号に着目して放物線と $x$ 軸との位置関係を調べると、次のようにまとめることができる。

$a\gt0$ の図
$a\gt0$ の図
$a\lt0$ の図
$a\lt0$ の図

以上の結果について、$x$ 軸との共有点の数だけに着目すれば、$a$ の正負によらず次のようにまとめられる。

判別式 $D$ と放物線の関係

  1. $\boldsymbol{D\gt0}$ のとき
    放物線 $y=f(x)$ は $x$ 軸と「2つの共有点をもつ」
  2. $\boldsymbol{D=0}$ のとき
    放物線 $y=f(x)$ は $x$ 軸と「1つの共有点をもつ」
    このとき、この放物線 $y=f(x)$ は $x$ と接する (contact) といい、この共有点のことを、特に、接点 (point of contact) という。
    この接点の座標は、放物線の頂点に等しく、$\left(-\dfrac{b}{2a},~0\right)$ である。
  3. $\boldsymbol{D\lt0}$ のとき
    放物線 $y=f(x)$ は $x$ 軸と「共有点をもたない」

$x$ 軸との共有点の個数の判別

2次関数 $y=x^2-(k-1)x+\dfrac{1}{4}k^2+k+1$ のグラフと $x$ 軸との共有点の個数は、定数 $k$ の値によってどのように変わるか調べよ。

$k$ の値によるグラフの変化
$k$ の値によるグラフの変化

2次関数 $y=x^2-(k-1)x+\dfrac{1}{4}k^2+k+1$ の判別式を $D$ とすると \begin{align} D=&(k-1)^2-4\left(\dfrac{1}{4}k^2+k+1\right)\\ =&k^2-2k+1-k^2-4k-4=-6k-3 \end{align}

  1. $-6k-3\gt0$、つまり $k\lt-\dfrac{1}{2}$ のとき
    $D\gt0$ となり、グラフは $x$ 軸と異なる2点で交わる。
  2. $-6k-3=0$、つまり $k=-\dfrac{1}{2}$ のとき
    $D=0$ となり、グラフは $x$ 軸と接する。
  3. $-6k-3\lt0$、つまり $k\gt-\dfrac{1}{2}$ のとき
    $D\lt0$ となり、グラフは $x$ 軸と共有点をもたない。
以上i～iiiより、共有点の個数は次のようになる。
  • $\boldsymbol{k\lt\dfrac{1}{2}}$ のとき $\boldsymbol{2}$ 個
  • $\boldsymbol{k=\dfrac{1}{2}}$ のとき $\boldsymbol{1}$ 個
  • $\boldsymbol{k\gt\dfrac{1}{2}}$ のとき $\boldsymbol{0}$ 個