2項定理

$(a+b)^n$を展開するということ

$(a+b)^2$ を展開すると

\begin{align} (a+b)^2=a^2+2ab+b^2 \end{align}

また， $(a+b)^3$ を展開すると

\begin{align} (a+b)^3=a^3+3a^2b+3ab^2+b^3 \end{align}

である．

ここでは，自然数 $n$ について， $(a+b)^n$ を展開した式を組合せを使って求める方法について考えてみよう． 以下では例として， $(a+b)^5$ の展開についてみていこう．

$(a+b)^5$ とは，5つの $(a+b)$ の積

のことである．この展開式は，5つの $(a+b)$ のそれぞれから， $a$ か $b$ のどちらかをとって，掛け合わせたものの和になる．

$a^4b$の係数はいくつになるのか

5つの $(a+b)$ のうち，1つから $b$ を選び，残りの4つから $a$ をとって掛け合わせると， $a^4b$ が作られる．

図は，①から $b$ をとった場合のイメージである．

ここで， $a^4b$ が作られる場合の数は，上の①から⑤の1ヶ所から $b$ を選べばよいので，組合せの考えを使って $_{5}\mathrm{C}_{1}$ と数えることができる．

つまり， $(a+b)^5$ の展開式における $a^4b$ の係数は $_{5}\mathrm{C}_{1}=5$ である．

$a^3b^2$の係数はいくつになるのか

5つの $(a+b)$ のうち，2つから $b$ を選び，残りの3つから $a$ をとって掛け合わせると， $a^3b^2$ が作られる．

図は，②と⑤から $b$ をとった場合のイメージである．

ここで， $a^3b^2$ が作られる場合の数は，上の①から⑤の2ヶ所から $b$ を選べばよいので，組合せの考えを使って $_{5}\mathrm{C}_{2}$ と数えることができる．

つまり， $(a+b)^5$ の展開式における $a^3b^2$ の係数は $_{5}\mathrm{C}_{2}=\dfrac{5\cdot4}{2\cdot1}=10$ である．

$(a+b)^5$の展開式

以上の例から， $(a+b)^5$ の展開式における各項の係数は，それぞれ次のようになるのがわかる．

$a^5$ の係数は5つの $(a+b)$ のうち0ヶ所から $b$ を選ぶと考えて $_{5}\mathrm{C}_{0}$

$a^4b$ の係数は5つの $(a+b)$ のうち1ヶ所から $b$ を選ぶと考えて $_{5}\mathrm{C}_{1}$

$a^3b^2$ の係数は5つの $(a+b)$ のうち2ヶ所から $b$ を選ぶと考えて $_{5}\mathrm{C}_{2}$

$a^2b^3$ の係数は5つの $(a+b)$ のうち3ヶ所から $b$ を選ぶと考えて $_{5}\mathrm{C}_{3}$

$ab^4$ の係数は5つの $(a+b)$ のうち4ヶ所から $b$ を選ぶと考えて $_{5}\mathrm{C}_{4}$

$b^5$ の係数は5つの $(a+b)$ のうち5ヶ所から $b$ を選ぶと考えて $_{5}\mathrm{C}_{5}$

つまり

\begin{align} (a+b)^5&=\ _{5}\mathrm{C}_{0}a^5+\ _{5}\mathrm{C}_{1}a^4b+\ _{5}\mathrm{C}_{2}a^3b^2\\ &\qquad+\ _{5}\mathrm{C}_{3}a^2b^3+\ _{5}\mathrm{C}_{4}ab^4+\ _{5}\mathrm{C}_{5}b^5 \end{align}

となる．

$(a+b)^n$の展開式(2項定理)

一般に， $(a+b)^n$ の展開式における $a^{n−r}b^r$ の係数は， $n$ 個の $(a+b)$ のうち， $r$ 個から $b$ を，残りの $n−r$ 個から $a$ を取り出す方法の総数 $_{n}\mathrm{C}_{r}$ となる．このことから，次の式(2項定理(binomial theorem))が成り立つことがわかる．

2項定理

$n$ を自然数とするとき， $(a+b)^n$ は

\begin{align} (a+b)^n&=\ _{n}\mathrm{C}_{0}a^n+\ _{n}\mathrm{C}_{1}a^{n-1}b+\cdots\\ &\qquad+\ _{n}\mathrm{C}_{n-1}ab^{n-1}+\ _{n}\mathrm{C}_{n}b^n \end{align}

と展開できる．

2項定理の係数になるという意味で，組合せの総数 $_{n}\mathrm{C}_{r}$ のことを2項係数(binomial coefficient)ともいう．

例えば， $(a+2b)^4$ は2項定理を用いて

\begin{align} &(a+2b)^4\\ =&\ _{4}\mathrm{C}_{0}a^4+\ _{4}\mathrm{C}_{1}a^3(2b)+\ _{4}\mathrm{C}_{2}a^2(2b)^2\\ &\qquad+\ _{4}\mathrm{C}_{3}a(2b)^3+\ _{4}\mathrm{C}_{4}(2b)^4\\ =&\ a^4+4a^3(2b)+6a^2(2b)^2+4a(2b)^3+(2b)^4\\ =&\ a^4+8a^3b+24a^2b^2+32ab^3+16b^4 \end{align}

と展開できる．

展開された式の係数

次の展開式において， $\left[\quad\right]$ 内で指定された項の係数を求めよ．

  1. $(2x+1)^6\qquad[x^2]$
  2. $(2x-3y)^5\qquad[x^3y^2]$
  3. $\left(x^2-\dfrac{1}{2x}\right)^7\qquad\left[\frac{1}{x}\right]$
  4. $\left(x-\dfrac{1}{2x^2}\right)^{12}\qquad[定数項]$

  1. $(2x+1)^6$ を展開したとき， $x^2$ を含む項は
    2. \begin{align} _{6}\mathrm{C}_{4}(2x)^21^4 \end{align}

    $\uparrow$ 2項定理を部分的に使った

    となる．よって， $x^2$ の係数は

    \begin{align} _{6}\mathrm{C}_{4}\cdot2^2=\boldsymbol{60} \end{align}
  2. $(2x−3y)^5$ を展開したとき， $x^3y^2$ を含む項は
    3. \begin{align} _{5}\mathrm{C}_{2}(2x)^3(-3y)^2 \end{align}

    $\uparrow$ 2項定理を部分的に使った

    となる．よって， $x^3y^2$ の係数は \begin{align} _{5}\mathrm{C}_{2}\cdot2^3\cdot(-3)^2=\boldsymbol{720} \end{align}

  3. $(a+b)^7$ の展開において， $a=x^2,b=-\dfrac{1}{2x}$ としたものが $\left(x^2-\dfrac{1}{2x}\right)^7$ である． $a^2b^5$ を計算すると $\dfrac{1}{x}$ の項ができるので，このときの係数を求める．
    4. \begin{align} &_{7}\mathrm{C}_{5}a^2b^5\\ =\ &_{7}\mathrm{C}_{5}(x^2)^2\left(-\frac{1}{2x}\right)^5\\ =\ &_{7}\mathrm{C}_{5}\left(-\frac{1}{2}\right)^5\frac{1}{x}\\ =\ &-\frac{21}{32}\cdot\frac{1}{x} \end{align}

    $\uparrow$ 2項定理を部分的に使った

    よって，求める係数は $\boldsymbol{-\dfrac{21}{32}}$である．

  4. $(a+b)^{12}$ の展開において， $a=x,b=-\dfrac{1}{2x^2}$ としたものが $\left(x-\dfrac{1}{2x^2}\right)^{12}$ である． $a^8b^4$ を計算すると定数項ができるので，このときの係数を求める．

    \begin{align} &_{12}\mathrm{C}_{4}a^8b^4\\ =\ &_{12}\mathrm{C}_{4}x^8\left(-\frac{1}{2x^2}\right)^4\\ =\ &_{12}\mathrm{C}_{4}\left(-\frac{1}{2}\right)^4\\ =\ &\frac{495}{16} \end{align}

    $\uparrow$ 2項定理を部分的に使った

    よって，求める係数は $\boldsymbol{\dfrac{495}{16}}$ である．

2項定理の応用

次の展開式において， $[\quad]$ 内で指定された項の係数を求めよ．

  1. $(2x+y-z)^8\qquad[x^2y^3z^3]$
  2. $(x-2y-z)^5\qquad[x^2yz^2]$

  1. $(2x+y-z)^8=\left\{2x+(y-z)\right\}^8$ として考える．

    2. これを展開したとき， $x^2$ の項は

    \begin{align} _{8}\mathrm{C}_{6}(2x)^2(y-z)^6 \end{align}

    $\uparrow$ 2項定理を部分的に使った

    として計算される．

    さらに $(y−z)^6$ を展開したとき， $y^3$ の項は

    \begin{align} _{6}\mathrm{C}_{3}y^3(-x)^3 \end{align}

    $\uparrow$ 2項定理を部分的に使った

    として計算される．

    よって， $(2x+y-z)^8$ を展開したときの $x^2y^3z^3$ の係数は

    \begin{align} &_{8}\mathrm{C}_{6}\cdot\ 2^2\cdot\ _{6}\mathrm{C}_{3}\cdot(-1)^3\\ =\ &-4\cdot\ _{8}\mathrm{C}_{2}\cdot\ _{6}\mathrm{C}_{3}=\boldsymbol{-2240} \end{align}
  2. $(x-2y-z)^5=\left\{x+(-2y-z)\right\}^5$ として考える． これを展開したとき， $x^2$ の項は
    3. \begin{align} _{5}\mathrm{C}_{3}x^2(-2y-z)^3 \end{align}

    $\uparrow$ 2項定理を部分的に使った

    として計算される．

    さらに $(−2y−z)^3$ を展開したとき， $y$ の項は

    \begin{align} _{3}\mathrm{C}_{2}(-2y)(-z)^2 \end{align}

    $\uparrow$ 2項定理を部分的に使った

    として計算される．

    よって， $(x−2y−z)^8$ を展開したときの $x^2yz^2$ の係数は

    \begin{align} \ &_{5}\mathrm{C}_{3}\cdot\ _{3}\mathrm{C}_{2}\cdot(-2)\cdot(-1)^2\\ =\ &-2\cdot\ _{5}\mathrm{C}_{2}\cdot\ _{3}\mathrm{C}_{1}=\boldsymbol{-60} \end{align}

2項係数の和

2項定理を用いて次の等式を証明せよ．

  1. \begin{align} 2^n=&\ _{n}\mathrm{C}_{0}+\ _{n}\mathrm{C}_{1}+\ _{n}\mathrm{C}_{2}+\cdots\\ &\qquad+\ _{n}\mathrm{C}_{n-1}+\ _{n}\mathrm{C}_{n} \end{align}
  2. \begin{align} 0=&\ _{n}\mathrm{C}_{0}-\ _{n}\mathrm{C}_{1}+\ _{n}\mathrm{C}_{2}-\cdots\\ &\qquad+(-1)^{n-1}\ _{n}\mathrm{C}_{n-1}+(-1)^n\ _{n}\mathrm{C}_{n} \end{align}
  3. \begin{align} (-1)^n=&\ _{n}\mathrm{C}_{0}-2\ _{n}\mathrm{C}_{1}+2^2\ _{n}\mathrm{C}_{2}-\cdots\\ &+(-2)^{n-1}\ _{n}\mathrm{C}_{n-1}+(-2)^n\ _{n}\mathrm{C}_{n} \end{align}

2項定理

\begin{align} &\ (a+b)^n\\ =&\ _{n}\mathrm{C}_{0}a^n+\ _{n}\mathrm{C}_{1}a^{n-1}b+\ _{n}\mathrm{C}_{2}a^{n-2}b^2+\cdots\\ &\qquad+\ _{n}\mathrm{C}_{n-1}ab^{n-1}+\ _{n}\mathrm{C}_{n}b^n \end{align}

において

  1. $a=b=1$ とおくと
    2. \begin{align} 2^n=&\ _{n}\mathrm{C}_{0}+\ _{n}\mathrm{C}_{1}+\ _{n}\mathrm{C}_{2}+\cdots\\ &\qquad+\ _{n}\mathrm{C}_{n-1}+\ _{n}\mathrm{C}_{n} \end{align}

    となり，確かに成立する．

  2. $a=1,b=−1$ とおくと
    3. \begin{align} 0=&\ _{n}\mathrm{C}_{0}-\ _{n}\mathrm{C}_{1}+\ _{n}\mathrm{C}_{2}-\cdots\\ &+(-1)^{n-1}\ _{n}\mathrm{C}_{n-1}+(-1)^n\ _{n}\mathrm{C}_{n} \end{align}

    となり，確かに成立する．

  3. $a=1,b=−2$ とおくと
    4. \begin{align} &\ (-1)^n\\ =&\ _{n}\mathrm{C}_{0}-2\ _{n}\mathrm{C}_{1}+2^2\ _{n}\mathrm{C}_{2}-\cdots\\ &\qquad+(-2)^{n-1}\ _{n}\mathrm{C}_{n-1}+(-2)^n\ _{n}\mathrm{C}_{n} \end{align}

    となり，確かに成立する．

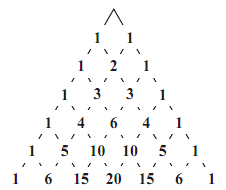
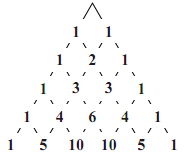
パスカルの三角形

図のように，2項係数 $_{n}\mathrm{C}_{0},\ _{n}\mathrm{C}_{1},\ _{n}\mathrm{C}_{2},\cdots,\ _{n}\mathrm{C}_{n}$ の値を，上から順に $n=1,2,3,\cdots$ の場合について三角形の形に並べたものを，パスカルの三角形(Pascal's triangle)という．

パスカルの三角形には，次のような特徴がある．

  1. $_{n}\mathrm{C}_{0}=\ _{n}\mathrm{C}_{n}=1$ であるから，各行の左右両端の数字は1である．
  2. $_{n}\mathrm{C}_{r}=\ _{n}\mathrm{C}_{n−r}$ であるから，各行は左右対称である．
  3. $_{n}\mathrm{C}_{r}=\ _{n−1}\mathrm{C}_{r-1}+\ _{n−1}\mathrm{C}_{r}$ であるから $_{n}\mathrm{C}_{r}$ の性質，左右両端以外の数字は，その左上の数と右上の数を足したものとなる．

パスカルの三角形

パスカルの三角形を利用して，次の展開式を求めよ．

  1. $(x+y)^6$
  2. $(x−2y)^5$

  1. パスカルの三角形を $n=6$ の場合まで書くと，図のようになるので
    2. \begin{align} &\ (x+y)^6\\ =&\ \boldsymbol{x^6+6x^5y+15x^4y^2+20x^3y^3}\\ &\ \qquad\qquad\boldsymbol{+15x^2y^4+6xy^5+y^6} \end{align}
  2. パスカルの三角形を $n=5$ の場合まで書くと，図のようになるので
    3. \begin{align} &\ (x-2y)^5\\ =&\ x^5+5x^4(-2y)+10x^3(-2y)^2\\ &\ +10x^2(-2y)^3+5x(-2y)^4+(-2y)^5\\ =&\ \boldsymbol{x^5-10x^4y+40x^3y^2}\\ &\ \boldsymbol{-80x^2y^3+80xy^4-32y^5} \end{align}