角の2等分線
内分と外分
内分と外分
内分
説明文
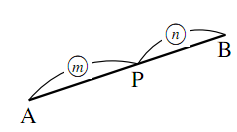
正の数 $m,n$ とする.線分 $\text{AB}$ 上の点 $\text{P}$ について
\[AP:PB=m:n\]が成り立つとき,点 $\text{P}$ は線分 $\text{AB}$ を $m:n$ に
内分(interior devision)
するといい, 点 $\text{P}$ のことを内分点という.
外分
正の数 $m,n$ とする.線分ABの延長上の点 $\text{Q}$ について
\[AQ:QB=m : n\]が成り立つとき,点 $\text{Q}$ は線分 $\text{AB}$ を $m:n$ に
外分(exterior devision)
するといい,点 $\text{Q}$ のことを外分点という.
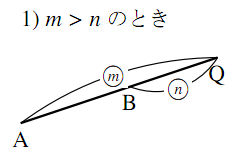
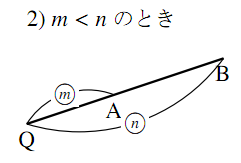
下図のように,点 $\text{Q}$ は
- $m\gt n$ のときは,線分 $\text{AB}$ の $\text{B}$ の方向への延長上
- $m\lt n$ のときは,線分 $\text{AB}$ の $\text{A}$ の方向への延長上
にある.
説明文
説明文
内分と外分
次の線分 $\text{AB}$ において,次の点を図示せよ.
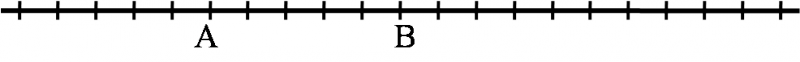
- $\text{AB}$ を $1:4$ に内分する点 $\text{P}$
- $\text{AB}$ を $3:2$ に外分する点 $\text{Q}$
- $\text{AB}$ を $3:2$ に内分する点 $\text{R}$
- $\text{AB}$ を $1:2$ に外分する点 $\text{S}$
角の2等分線の定理(幾何)
角の2等分線の定理
角の2等分線の定理
説明文
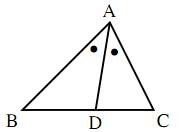
$\triangle{\mathrm{ABC}}$ において, $\angle{\mathrm{A}}$ の2等分線と辺 $\text{BC}$ との交点を $\text{D}$ とするとき
\[\text{AB}:\text{AC}=\text{BD}:\text{DC}\]が成り立つ.
証明
角の2等分線の定理
説明文

次の図の $\triangle{\mathrm{ABC}}$ において,点 $\text{D}$ は $\angle{\text{A}}$ の二等分線と辺 $\text{BC}$ との交点である.このとき,線分 $\text{BD}$ の長さを求めよ.
$BD=x$ とおくと,角の二等分線の定理より,
\begin{align} AB:AC&=BD:DC\\ 5:4&=x:(18-x)\\ 4x&=5(18-x)\\ 9x&=90\\ x&=10\\ \therefore\ \boldsymbol{BD}&=\boldsymbol{10} \end{align}三角形の外角の二等分線と比
説明文

$\triangle{\mathrm{ABC}}$ において, $\angle{\mathrm{A}}$ の外角の二等分線と辺 $\text{BC}$ の延長線との交点を $\text{D}$ とするとき
\[\text{AB}:\text{AC}=\text{BD}:\text{DC}\]が成り立つ.
三角形の外角の二等分線と比
説明文

次の図の $\triangle{\mathrm{ABC}}$ において,点Dは $\angle{\mathrm{A}}$ の外角の二等分線と半直線 $\text{BC}$ との交点である.このとき,線分 $\text{CD}$ の長さを求めよ.
$CD=x$ とおくと,外角の二等分線の定理より,
\begin{align} AB:AC&=BD:DC\\ 7:5&=(6+x):x\\ 7x&=5(6+x)\\ 2x&=30\\ x&=15\\ \therefore\ \boldsymbol{CD}&=\boldsymbol{15} \end{align}