メネラウスの定理
メネラウスの定理
メネラウスの定理
メネラウスの定理
無題
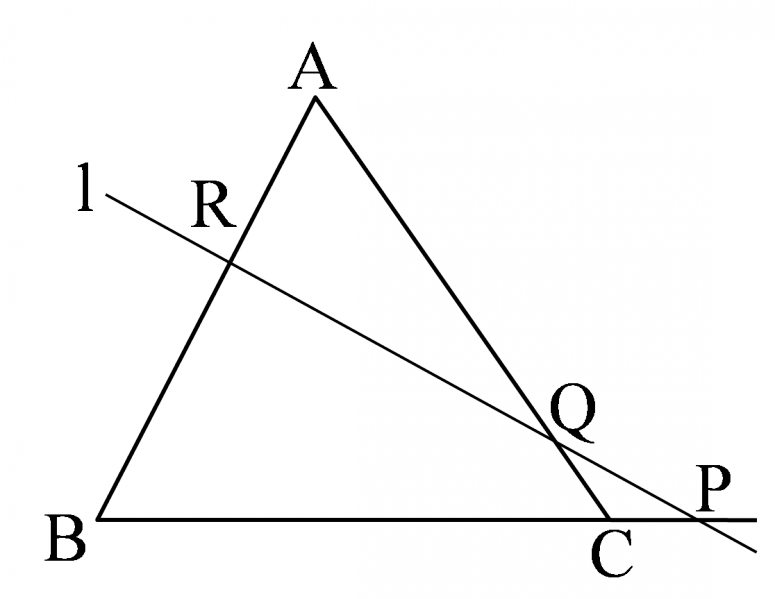
$\triangle{\mathrm{ABC}}$ の辺 $\mathrm{BC},\mathrm{CA},\mathrm{AB}$ またはその延長が,三角形の頂点を通らない直線 $\text{l}$ と,それぞれ点 $\mathrm{P},\mathrm{Q},\mathrm{R}$ で交わるとき
\[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}}=1\]証明
メネラウスの定理
無題
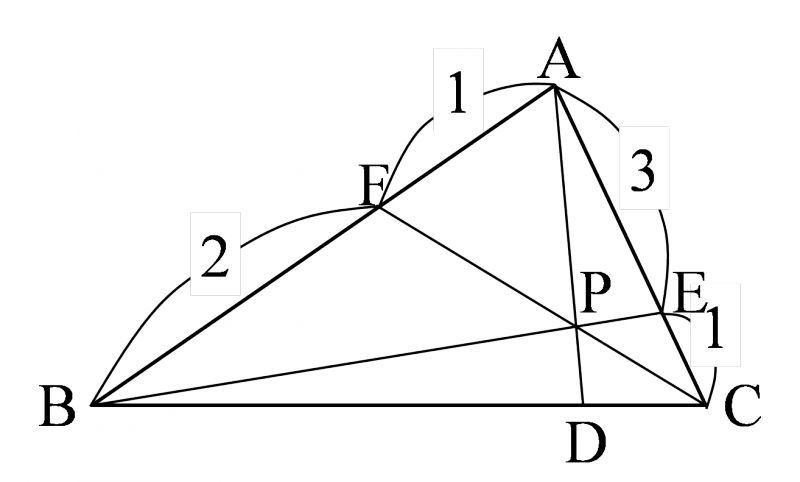
$\triangle{\mathrm{ABC}}$ において,辺 $\text{AC}$ を $3:1$ の比に内分する点を $\text{E}$ ,辺 $\text{AB}$ を $1:2$ の比に内分する点を $\text{F}$ とし, $\text{BE}$ と $\text{CF}$ の交点を $\text{P}$ , $\text{AP}$ と $\text{BC}$ の交点を $\text{D}$ とする.このとき,次のものを求めよ.
- $BD:DC$
- $AP:PD$
- $CP:PF$
- $\triangle{\mathrm{ABP}}:\triangle{\mathrm{ABC}}$
- チェバの定理より, \[\frac{\text{BD}}{\text{DC}}\cdot\frac{\text{CE}}{\text{EA}}\cdot\frac{\text{AF}}{\text{FB}}=1,\frac{\text{BD}}{\text{DC}}\cdot\frac{1}{3}\cdot\frac{1}{2}=1\]
- $\triangle{\mathrm{ADC}}$ と直線 $\text{BE}$ にメネラウスの定理を用いると, \[\frac{\text{DB}}{\text{BC}}\cdot\frac{\text{CE}}{\text{EA}}\cdot\frac{\text{AP}}{\text{PD}}=1,\frac{6}{7}\cdot\frac{1}{3}\cdot\frac{\text{AP}}{\text{PD}}=1\]
- $\triangle{\mathrm{ACF}}$ と直線 $\text{BE}$ にメネラウスの定理を用いると, \[\frac{\text{CP}}{\text{PF}}\cdot\frac{\text{FB}}{\text{BA}}\cdot\frac{\text{AE}}{\text{EC}}=1,\frac{\text{CP}}{\text{PF}}\cdot\frac{2}{3}\cdot\frac{3}{1}=1\]
- $AP:PD=7:2$ より, $\triangle{\mathrm{ABP}}=\dfrac{7}{9}\triangle{\mathrm{ABD}}$
よって,
\[BD:DC=\boldsymbol{6:1}\]よって,
\[AP:PD=\boldsymbol{7:2}\]よって,
\[CP:PF=\boldsymbol{1:2}\]$BD:DC=6:1$ より, $\triangle{\mathrm{ABD}}=\dfrac{6}{7}\triangle{\mathrm{ABC}}$
よって, $\triangle{\mathrm{ABP}}=\dfrac{7}{9}\times\dfrac{6}{7}\triangle{\mathrm{ABC}}=\dfrac{2}{3}\triangle{\mathrm{ABC}}$
ゆえに, $\triangle{\mathrm{ABP}}:\triangle{\mathrm{ABC}}=\boldsymbol{2:3}$