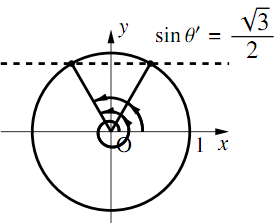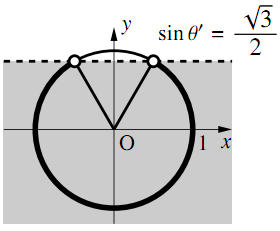三角関数の定義

三角関数の定義について

三角関数の定義について

FTEXT 数学Iで学んだ三角比(trigonometric ratio) で扱う角を任意の実数 とすれば，次の三角関数(trigonometric function) の定義となる．

三角関数の定義

無題

無題

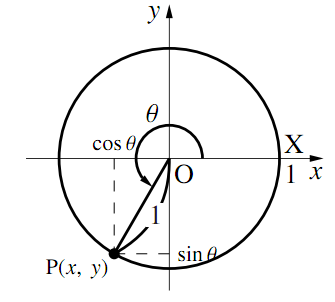
単位円周と動径の交点を$\text{P},\text{X}(1,~0)$とする．

$\angle{\text{POX}}=\theta$($\theta$は任意の実数)とするとき

$\cos\theta = $(動点$\text{P}$の$x$座標)

$\sin\theta = $(動点$\text{P}$の$y$座標)

$\tan\theta =$ (動点$\text{P}$の$y$座標)$/$(動点$\text{P}$の$x$座標)$=$(動径$\text{OP}$の傾き)

とする． ただし，動点$\text{P}$の$x$座標が$0$のとき， つまり$\theta=\dfrac{\pi}{2} +n\pi$($n$は整数) のときは$\tan\theta$は定義されない．

（注） （注）

具体的な例で確認してみよう．

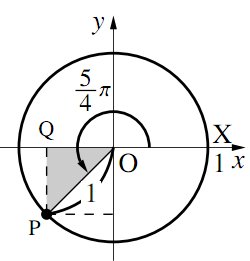
三角関数の定義についての図その１

1)$\theta=\dfrac{5}{4}\pi$のとき

$\triangle{\text{OPQ}}$は$\text{PQ}:\text{QO}:\text{OP}=1:1:\sqrt{2}$の直角三角形である．つまり，$\text{P}\left(-\dfrac{\sqrt{2}}{2},~-\dfrac{\sqrt{2}}{2}\right)$なので

\begin{align} &\cos\dfrac{5}{4}\pi=-\dfrac{\sqrt{2}}{2},~~~\\ &\sin\dfrac{5}{4}\pi=-\dfrac{\sqrt{2}}{2},~~~\\ &\tan\dfrac{5}{4}\pi=1 \end{align}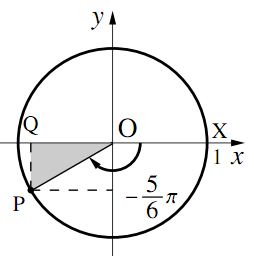
三角関数の定義についての図その２

2)$\theta=-\dfrac{5}{6}\pi$のとき

$\triangle{\text{OPQ}}$は$\text{PQ}:\text{QO}:\text{OP}=1:\sqrt{3}:2$の直角三角形である．つまり，$\text{P}\left(-\dfrac{\sqrt{3}}{2},~-\dfrac{1}{2}\right)$なので

\begin{align} &\cos\left(-\dfrac{5}{6}\pi\right)=-\dfrac{\sqrt{3}}{2},~~~\\ &\sin\left(-\dfrac{5}{6}\pi\right)=-\dfrac{1}{2},~~~\\ &\tan\left(-\dfrac{5}{6}\pi\right)=\dfrac{1}{\sqrt{3}} \end{align}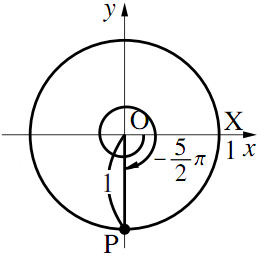
三角関数の定義についての図その３

3)$\theta=-\dfrac{5}{2}\pi$のとき

$-\dfrac{5}{2}\pi=-\dfrac{1}{2}\pi -2\pi$より， $\text{X}$から負の方向へ$-\dfrac{1}{2}\pi$移動した$(0,~-1)$に$\text{P}$があるので

\begin{align} &\cos\left(-\dfrac{5}{2}\pi\right)=0,~\\ &\sin\left(-\dfrac{5}{2}\pi\right)=-1,~\\ &\tan\left(-\dfrac{5}{2}\pi\right) \end{align} は定義できない

$\tan\theta$には次のような意味もあることを理解しておこう．

$\tan\theta$の図形的意味

無題

無題

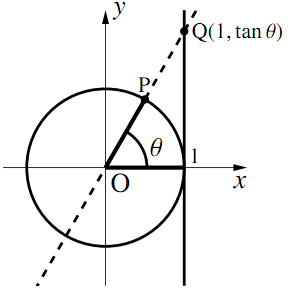
$\tan\theta$の定義は，動径$\text{OP}$の傾きであるが，傾きとは$x$軸方向に$1$増加するときの$y$軸方向の増加量である． そのため，図のように直線$\text{OP}$と直線$x = 1$の交点を$\text{Q}$とすると，$\text{Q}$の$y$座標が$\tan\theta$になる．

三角関数の定義域と値域

三角関数の定義域と値域

以上のことから，三角関数の定義域と値域は次のようにまとめられる．

三角関数の定義域と値域

  1. 三角関数の定義域

    1. $\sin\theta,\cos\theta$の$\theta$は，任意の実数をとることができる．

    2. $\tan\theta$の$\theta$は，$\dfrac{\pi}{2}+n\pi$($n$は整数)以外の任意の実数をとることができる．

  2. 三角関数の値域

    1. 任意の実数$\theta$に対し，$\sin\theta,\cos\theta$は$ − 1$以上$1$以下の値をとる．

    2. $\dfrac{\pi}{2}+n\pi$($n$は整数)以外の任意の実数$\theta$に対し，$\tan\theta$は任意の実数をとる．

三角関数の符号と動径の象限

三角関数の符号と動径の象限

三角関数の値の符号は，その角の動径がどの象限に含まれるかで決定する． まとめると次のようになる．

三角関数の符号と動径の象限

三角関数の値の符号は，動径のある象限によって次のように決まる．

1)$\sin\theta$の符号

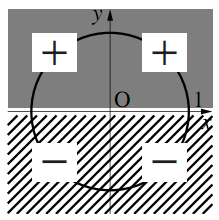
三角関数の符号と動径の象限の図その１

2)$\cos\theta$の符号

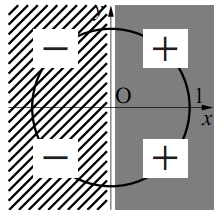
三角関数の符号と動径の象限の図その２

3)$\tan\theta$の符号

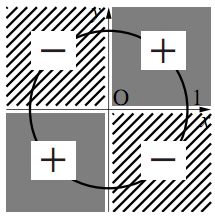
三角関数の符号と動径の象限の図その３

任意の角に対する三角関数の値

以下の角度に対する，正弦，余弦，正接の値をそれぞれ求めよ．

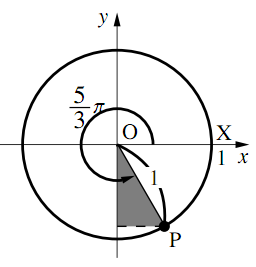
  1. $\dfrac{5}{3}\pi$
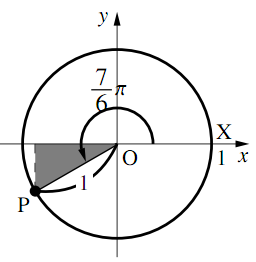
  2. $\dfrac{7}{6}\pi$
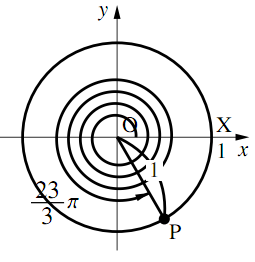
  3. $\dfrac{23}{3}\pi$
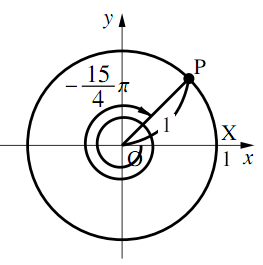
  4. $-\dfrac{15}{4}\pi$

    任意の角に対する三角関数の値の解答の図その１


  1. $\text{P}~\left(\dfrac{1}{2},~-\dfrac{\sqrt{3}}{2}\right)$なので

    $\boldsymbol{\cos\dfrac{5}{3}\pi=\dfrac{1}{2}}$

    $\boldsymbol{\sin\dfrac{5}{3}\pi=-\dfrac{\sqrt{3}}{2}}$

    $\boldsymbol{\tan\dfrac{5}{3}\pi=-\sqrt{3}}$

    2. 任意の角に対する三角関数の値の解答の図その２


  2. $\text{P}~\left(-\dfrac{\sqrt{3}}{2},~ -\dfrac12\right)$なので

    $\boldsymbol{\cos\dfrac{7}{6}\pi=-\dfrac{\sqrt{3}}{2}}$

    $\boldsymbol{\sin\dfrac{7}{6}\pi=-\dfrac{1}{2}}$

    $\boldsymbol{\tan\dfrac{7}{6}\pi=\dfrac{\sqrt{3}}{3}}$

    3. 任意の角に対する三角関数の値の解答の図その３


  3. $\dfrac{23}{3}\pi=\dfrac{5}{3}\pi +3\cdot 2\pi$より，$\dfrac{5}{3}\pi$の三角関数に等しい．1.より

    $\boldsymbol{\cos\dfrac{23}{3}\pi=\dfrac{1}{2}}$

    $\boldsymbol{\sin\dfrac{23}{3}\pi=-\dfrac{\sqrt{3}}{2}}$

    $\boldsymbol{\tan\dfrac{23}{3}\pi=-\sqrt{3}}$

    4. 任意の角に対する三角関数の値の解答の図その４


  4. $-\dfrac{15}{4}\pi=\dfrac{1}{4}\pi +(-2)\cdot 2\pi$より，$\dfrac{1}{4}\pi$の三角関数に等しい．よって

    $\boldsymbol{\cos\left(-\dfrac{15}{4}\pi\right)=\dfrac{\sqrt{2}}{2}}$

    $\boldsymbol{\sin\left(-\dfrac{15}{4}\pi\right)=\dfrac{\sqrt{2}}{2}}$

    $\boldsymbol{\tan\left(-\dfrac{15}{4}\pi\right)=1}$

三角関数を含む方程式

  1. $0\leqq \theta<2\pi$のとき，$\sin\theta =-\dfrac{1}{2}$を満たす$\theta$を求めよ．
  2. $0\leqq \theta<4\pi$のとき，$\sin\theta =-\dfrac{1}{2}$を満たす$\theta$を求めよ．
  3. $\theta$を任意の実数とする．$\sin\theta =-\dfrac{1}{2}$を満たす$\theta$を求めよ．
  4. $-\pi\leqq \theta<\pi$のとき，$\sin\theta =-\dfrac{1}{2}$を満たす$\theta$を求めよ．

無題
無題

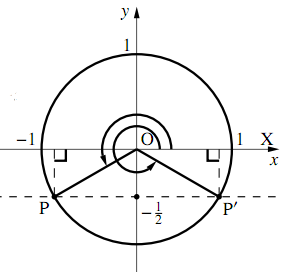
(動点の$y$座標の値)$=-\dfrac{1}{2}$であればよいので，求める$\theta$は，図の$\angle{\text{POX}},~\angle{\text{P}’\text{OX}}$に等しい．

  1. $0\leqq \theta < 2\pi$の範囲では

    $\angle{\text{POX}}=\dfrac{7}{6}\pi,~~$

    $\angle{\text{P}’\text{OX}}=\dfrac{11}{6}\pi$

    となる．つまり，$\boldsymbol{\theta=\dfrac{7}{6}\pi,~\dfrac{11}{6}\pi}$．

  2. $0\leqq \theta < 4\pi$の範囲では

    \begin{align} &\angle{\text{POX}}=\dfrac{7}{6}\pi,~\dfrac{7}{6}\pi +2\pi\\ &\angle{\text{P}’\text{OX}}=\dfrac{11}{6}\pi,~\dfrac{11}{6}\pi +2\pi \end{align}

    となる．つまり，

    $\boldsymbol{\theta=\dfrac{7}{6}\pi,~\dfrac{11}{6}\pi,~\dfrac{19}{6}\pi,~\dfrac{23}{6}\pi}$．

  3. $\theta$は任意なので，$n$を整数として

    \begin{align} &\angle{\text{POX}}=\dfrac{7}{6}\pi +2n\pi,~~\\ &\angle{\text{P}’\text{OX}}=\dfrac{11}{6}\pi +2n\pi \end{align}

    となる．つまり，$ \boldsymbol{\theta=\dfrac{7}{6}\pi +2n\pi,~\dfrac{11}{6}\pi +2n\pi}$．

  4. $-\pi\leqq \theta < \pi$の範囲では

    \begin{align} &\angle{\text{POX}}=\dfrac{7}{6}\pi -2\pi,~~\\ &\angle{\text{P}’\text{OX}}=\dfrac{11}{6}\pi -2\pi \end{align}

    となる．つまり， $\boldsymbol{\theta=-\dfrac{5}{6}\pi,~ -\dfrac{1}{6}\pi}$．

三角関数を含む不等式

  1. $0\leqq \theta<2\pi$のとき，$\cos\theta <\dfrac{1}{2}$を満たす$\theta$の範囲を求めよ．
  2. $0\leqq \theta<4\pi$のとき，$\cos\theta <\dfrac{1}{2}$を満たす$\theta$の範囲を求めよ．
  3. $\theta$を任意の実数とする．$\cos\theta <\dfrac{1}{2}$を満たす$\theta$の範囲を求めよ．
  4. $-\pi\leqq \theta<\pi$のとき，$\cos\theta <\dfrac{1}{2}$を満たす$\theta$の範囲を求めよ．

無題
無題

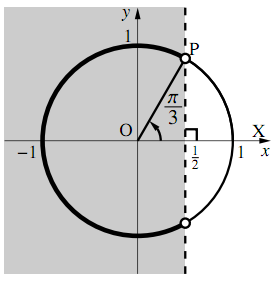
(動点の$x$座標の値)$<\dfrac{1}{2}$であればよい．

そのためには，動点が図の太線部分にあればよい．

  1. $0\leqq \theta < 2\pi$の範囲では， $\boldsymbol{\dfrac{1}{3}\pi<\theta<\dfrac{5}{3}\pi}$．

  2. $0\leqq \theta < 4\pi$の範囲では， 1.の答えに加えて

    $\dfrac{1}{3}\pi +2\pi <\theta<\dfrac{5}{3}\pi +2\pi$

    も満たすので， $\boldsymbol{\dfrac{1}{3}\pi <\theta<\dfrac{5}{3}\pi,~\dfrac{7}{3}\pi <\theta<\dfrac{11}{3}\pi}$．

  3. $\theta$は任意なので，

    $\boldsymbol{\dfrac{1}{3}\pi +2n\pi <\theta<\dfrac{5}{3}\pi +2n\pi~~}$($n$は整数)

    が求める答えとなる．

  4. $-\pi\leqq \theta < \pi$の範囲では

    \begin{align} -\pi \leqq \theta<\dfrac{5}{3}\pi -2\pi,~~ \dfrac{1}{3}\pi <\theta< \pi \end{align}

    となる．つまり， $\boldsymbol{-\pi \leqq \theta<-\dfrac{1}{3}\pi,~ \dfrac{1}{3}\pi <\theta<\pi}$．

範囲をもつ変数の置き換え

  1. $0\leqq \theta <2\pi,~\theta'=2 \theta -\dfrac{\pi}{3}$とする． $\theta'$のとりうる範囲を求めよ．
  2. $0\leqq \theta <2\pi$のとき， 方程式$\sin\left(2 \theta -\dfrac{\pi}{3}\right) =\dfrac{\sqrt{3}}{2}$を満たす$\theta$の値を求めよ．
  3. $0\leqq \theta <2\pi$のとき， 不等式$\sin\left(2 \theta -\dfrac{\pi}{3}\right) <\dfrac{\sqrt{3}}{2}$を満たす$\theta$の範囲を求めよ．

  1. \begin{align} &0\leqq \theta <2\pi\\ \Leftrightarrow~&0\leqq 2\theta <4\pi\\ \Leftrightarrow~&0-\dfrac{\pi}{3} \leqq 2\theta-\dfrac{\pi}{3} <4\pi-\dfrac{\pi}{3} \end{align}

    より$\boldsymbol{-\dfrac{\pi}{3} \leqq \theta' <\dfrac{11}{3}\pi}$と分かる．

    ←$2$倍しても，$\dfrac{\pi}{3}$を引いても大小関係は変わらない

    2. 範囲をもつ変数の置き換えの解答の図その１

  2. 1.の$ \theta'$を用いると，与えられた方程式は$\sin\theta' =\dfrac{\sqrt{3}}{2}$となる． 1.より$-\dfrac{\pi}{3} \leqq \theta' <\dfrac{11}{3}\pi$なので，図より

    $\theta' =\dfrac13\pi,~\dfrac23\pi,~\dfrac73\pi,~\dfrac83\pi$となる．

    $\theta=\dfrac{\theta'}{2}+\dfrac{\pi}{6}$なので

    \begin{align} \boldsymbol{\theta= \dfrac13\pi,~\dfrac12\pi,~\dfrac43\pi,~\dfrac32\pi} \end{align}
    3. 範囲をもつ変数の置き換えの解答の図その２

  3. 1.の$ \theta'$を用いると，与えられた不等式は$\sin\theta' <\dfrac{\sqrt{3}}{2}$となる． 1.より$-\dfrac{\pi}{3} \leqq \theta' <\dfrac{11}{3}\pi$なので

    $-\dfrac{\pi}{3}\leqq \theta' <\dfrac13\pi,~\dfrac23\pi< \theta' <\dfrac73\pi,$
    $~\dfrac83\pi< \theta' <\dfrac{11}{3}\pi$となる．$ \theta'=2\theta-\dfrac{\pi}{3}$を代入して$\theta$について解けば

    ←たとえば

    \begin{align} &\dfrac{2}{3}\pi< 2\theta-\dfrac{\pi}{3} <\dfrac{7}{3}\pi\\ \Leftrightarrow~&\pi< 2\theta<\dfrac83\pi ~\Leftrightarrow~\dfrac{\pi}{2}< \theta<\dfrac{4}{3}\pi \end{align} \begin{align} &\boldsymbol{0\leqq\theta< \dfrac{\pi}{3},~\dfrac{\pi}{2}<\theta<\dfrac43\pi,}\\ &\boldsymbol{\dfrac32\pi<\theta <2\pi} \end{align}