三角関数の性質

$\theta+2n\pi$の三角関数

$\pi+2n\pi$の三角関数

$n$が整数のとき，角$\theta+2n\pi$の動径は，角$\theta$の動径と一致するので，次の公式が成り立つ．

$\pi+\theta$の三角比

任意の角$\theta$について

\begin{align} &\sin(\theta+2n\pi)=\sin\theta\\ &\cos(\theta+2n\pi)=\cos\theta\\ &\tan(\theta+2n\pi)=\tan\theta \end{align}

が成り立つ．ただし，$n$は整数とする．

$-\theta$の三角関数

暗記$-\theta$の三角関数

$\sin(-\theta),\cos(-\theta),\tan(-\theta)$を，それぞれ$\sin\theta,\cos\theta,\tan\theta$で表せ．

$−\theta$ の三角関数の解答

無題

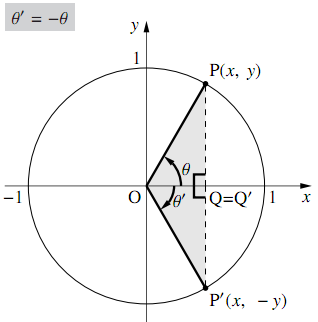
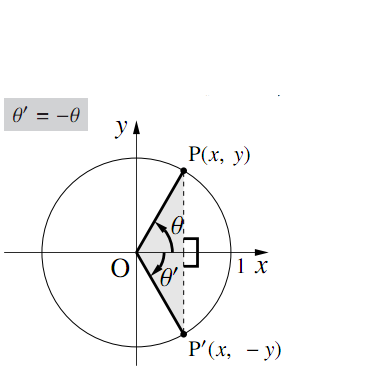
図のように，単位円周上に角$\theta$の動径$\text{OP}$と角 $-\theta$( $=\theta'$とする)の動径$\text{OP}'$をとる．

点$\text{P}$の座標を$(x,~y)$とすると，$ \triangle{\text{OPQ}}と\triangle{\text{OP}'\text{Q}'}$は合同なので，点$\text{P}'$の座標は$(x,~-y)$となるから

\begin{align} &\sin{\theta'}=-y=\boldsymbol{-\sin\theta}\\ &\cos{\theta'}=x=\boldsymbol{\cos\theta}\\ &\tan{\theta'}=\dfrac{-y}{x}=\boldsymbol{-\tan\theta} \end{align}

$-\theta$の三角比

無題

任意の角$\theta$について

\begin{align} &\sin(-\theta)=-\sin\theta\\ &\cos(-\theta)=\cos\theta\\ &\tan(-\theta)=-\tan\theta \end{align}

が成り立つ．

$\theta+\pi$の三角関数

暗記$\theta+\pi$の三角関数

$\sin(\theta+\pi),\cos(\theta+\pi),\tan(\theta+\pi)$を，それぞれ$\sin\theta,\cos\theta,\tan\theta$で表せ．

$\theta+\pi$の三角関数の解答

無題

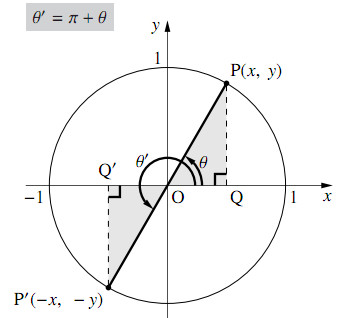
図のように，単位円周上に角$\theta$の動径$\text{OP}$と角$\pi +\theta$( $= \theta'$とする)の動径$\text{OP}'$をとる．

点$\text{P}$の座標を$(x,~y)$とすると， $\triangle{\text{OPQ}}と\triangle{\text{OP}'\text{Q}'}$は合同なので，点$\text{P}'$の座標は$(-x,~-y)$となるから

\begin{align} &\sin{\theta'}=-y=\boldsymbol{-\sin\theta}\\ &\cos{\theta'}=-x=\boldsymbol{-\cos\theta}\\ &\tan{\theta'}=\dfrac{-y}{-x}=\dfrac{y}{x}=\boldsymbol{\tan\theta} \end{align}

$\theta+\pi$の三角比

無題

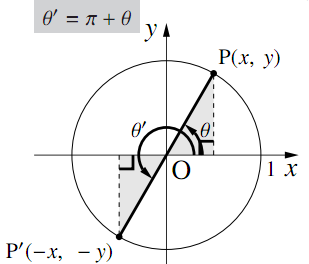
任意の角$\theta$について

\begin{align} &\sin(\theta+\pi)=-\sin\theta\\ &\cos(\theta+\pi)=-\cos\theta\\ &\tan(\theta+\pi)=\tan\theta \end{align}

が成り立つ．

$\theta+\dfrac{\pi}{2}$の三角関数

暗記$\theta+\dfrac{\pi}{2}$の三角関数

$\sin\left(\theta+\dfrac{\pi}{2}\right),\cos\left(\theta+\dfrac{\pi}{2}\right),\tan\left(\theta+\dfrac{\pi}{2}\right)$を，それぞれ$\sin\theta,\cos\theta,\tan\theta$で表せ．

$\theta+\dfrac{\pi}{2}$の三角関数の解答

無題

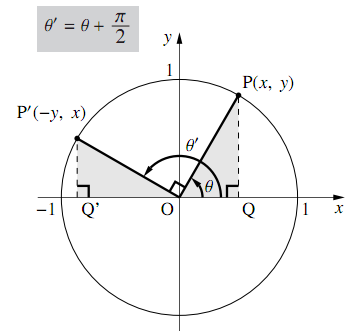
図のように，単位円周上に角$\theta$の動径$\text{OP}$と角$\theta+\dfrac{\pi}{2}$($ = \theta'$とする)の動径$\text{OP}'$をとる．

点$\text{P}$の座標を$(x,~y)$とすると，$ \triangle{\text{OPQ}}と\triangle{\text{OP}'\text{Q}'}$は合同なので，点$\text{P}'$の座標は$(-y,~x)$となるから

\begin{align} &\sin{\theta'}=x=\boldsymbol{\cos\theta}\\ &\cos{\theta'}=-y=\boldsymbol{-\sin\theta}\\ &\tan{\theta'}=\dfrac{x}{-y}=\boldsymbol{-\dfrac{1}{\tan\theta}} \end{align}

$\theta+\dfrac{\pi}{2}$の三角比

無題

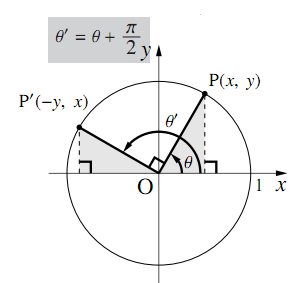
任意の角$\theta$について

\begin{align} &\sin\left(\theta+\dfrac{\pi}{2}\right)=\cos\theta\\ &\cos\left(\theta+\dfrac{\pi}{2}\right)=-\sin\theta\\ &\tan\left(\theta+\dfrac{\pi}{2}\right)=-\dfrac{1}{\tan\theta} \end{align}

が成り立つ．

吹き出し$\theta+\dfrac{\pi}{2}$の三角関数

この節で学んだ公式は丸暗記するようなものではない．図を書いてすぐに導けるように練習しておこう．