三角関数の加法定理

正弦と余弦の加法定理

正弦と余弦の加法定理

2つの角の和や差の三角関数は，それぞれの角の三角関数で表すことができる． まずはじめに

\begin{align} \cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta \end{align} $\tag{1}\label{seigentoyogennokahouteiri1}$

となることを証明してみよう．

【証明】

図のように，点$\text{P}(\cos\alpha,~\sin\alpha)$と点$\text{Q}(\cos\beta,~\sin\beta)$をとると， 2点間の距離の公式より

\begin{align} \text{PQ}^2&=(\cos\beta-\cos\alpha)^2+(\sin\beta-\sin\alpha)^2\\ &=2-2(\cos\alpha\cos\beta+\sin\alpha\sin\beta) \end{align}

である．

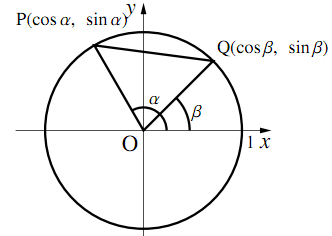
正弦と余弦の加法定理の図その１

次に，図のように，2点$\text{P}，\text{Q}$を原点を中心に$ − \beta$だけ回転させた図形を考える． このとき，動径$\text{OP}$のなす角は$\alpha − \beta$となるので，2点間の距離の公式より

\begin{align} \text{PQ}^2&=(1-\cos(\alpha-\beta))^2+\sin^2(\alpha-\beta)\\ &=2-2\cos(\alpha-\beta) \end{align}

よって

\begin{align} &2-2(\cos\alpha\cos\beta+\sin\alpha\sin\beta)\\ &=2-2\cos(\alpha-\beta)\\ \Leftrightarrow~&\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta \end{align}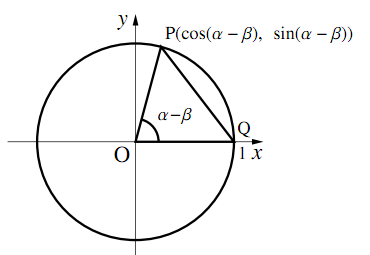
正弦と余弦の加法定理の図その２

暗記正弦と余弦の加法定理の導出

上の$\eqref{seigentoyogennokahouteiri1}$を利用して，次の等式を証明せよ．

  1. $\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$
  2. $\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta$
  3. $\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$

  1. $\eqref{seigentoyogennokahouteiri1}$で$\beta$を $− \beta$におきかえると

    \begin{align} &\cos\{\alpha-(-\beta)\}=\cos\alpha\cos(-\beta)\\ &\qquad\qquad\qquad+\sin\alpha\sin(-\beta)\\ \Leftrightarrow~&\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta \end{align}

    ← $-\theta$の三角比

  2. $\eqref{seigentoyogennokahouteiri1}$で$\beta$を$\beta-\dfrac{\pi}{2}$におきかえると

    \begin{align} &\cos\left\{\alpha-\left(\beta-\dfrac{\pi}{2}\right)\right\}\\ &\qquad=\cos\alpha\cos\left(\beta-\dfrac{\pi}{2}\right)\\ &\qquad+\sin\alpha\sin\left(\beta-\dfrac{\pi}{2}\right)\\ \Leftrightarrow~&\cos\left\{(\alpha-\beta)+\dfrac{\pi}{2}\right\}\\ &\qquad=\cos\alpha\cos\left(\beta-\dfrac{\pi}{2}\right)\\ &\qquad+\sin\alpha\sin\left(\beta-\dfrac{\pi}{2}\right)\\ \Leftrightarrow~&-\sin(\alpha-\beta)=\cos\alpha\sin\beta-\sin\alpha\cos\beta\\ \Leftrightarrow~&\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta \end{align}

  3. 2.で$\beta$を$ − \beta$におきかえると

    \begin{align} &\sin\left\{\alpha-(-\beta)\right\}=\sin\alpha\cos(-\beta)\\ &\qquad\qquad\qquad-\cos\alpha\sin(-\beta)\\ &\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta \end{align}

    ← $-\theta$の三角比

正弦と余弦の加法定理

\begin{align} 1)&\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\\ &\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta\\ 2)&\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\\ &\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta \end{align}

正弦と余弦の加法定理

  1. $45^\circ-30^\circ=15^\circ$であることに注意して，$\sin15^\circ$と$\cos15^\circ$の値を求めよ．

  2. $\dfrac{\pi}{4}+\dfrac{\pi}{6}=\dfrac{5}{12}\pi$であることに注意して$\sin\dfrac{5}{12}\pi$と$\cos\dfrac{5}{12}\pi$の値を求めよ．

  1. 加法定理をもちいて

    \begin{align} \sin15^\circ&=\sin(45^\circ-30^\circ)\\ &=\sin45^\circ\cos30^\circ-\cos45^\circ\sin30^\circ\\ &=\dfrac{\sqrt{2}}{2}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{2}\cdot\dfrac{1}{2}\\ &=\boldsymbol{\dfrac{\sqrt{6}-\sqrt{2}}{4}}\\ \cos15^\circ&=\cos(45^\circ-30^\circ)\\ &=\cos45^\circ\cos30^\circ+\sin45^\circ\sin30^\circ\\ &=\dfrac{\sqrt{2}}{2}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{2}\cdot\dfrac{1}{2}\\ &=\boldsymbol{\dfrac{\sqrt{6}+\sqrt{2}}{4}} \end{align}

  2. 加法定理をもちいて

    \begin{align} \sin\dfrac{5}{12}\pi&=\sin\left(\dfrac{\pi}{4}+\dfrac{\pi}{6}\right)\\ &=\sin\dfrac{\pi}{4}\cos\dfrac{\pi}{6}+\sin\dfrac{\pi}{4}\cos\dfrac{\pi}{6}\\ &=\dfrac{\sqrt{2}}{2}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{2}\cdot\dfrac{1}{2}\\ &=\boldsymbol{\dfrac{\sqrt{6}+\sqrt{2}}{4}}\\ \cos\dfrac{5}{12}\pi&=\cos\left(\dfrac{\pi}{4}+\dfrac{\pi}{6}\right)\\ &=\cos\dfrac{\pi}{4}\cos\dfrac{\pi}{6}-\sin\dfrac{\pi}{4}\sin\dfrac{\pi}{6}\\ &=\dfrac{\sqrt{2}}{2}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{2}\cdot\dfrac{1}{2}\\ &=\boldsymbol{\dfrac{\sqrt{6}-\sqrt{2}}{4}} \end{align}

三角関数の加法定理と平面図形

無題

無題

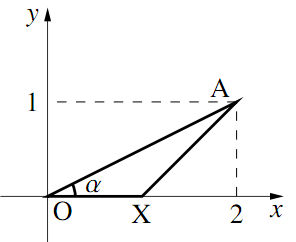
図のように$\text{X}(1,~0)$と$\text{A}(2,~1)$があり，$\angle{\text{AOX}}=\alpha$とする．

  1. $\cos\alpha,~\sin\alpha$の値を求めよ．

  2. $\triangle{\text{AOX}}$を$\text{O}$を中心に$\dfrac{\pi}{3}$回転移動し，$\triangle{\text{A}'\text{OX}'}$になったとする． このとき，$\text{X}'$，$\text{A}'$の座標を求めよ．

  1. $\text{OA}=\sqrt{5}$より，

    $\boldsymbol{\cos\alpha=\dfrac{2}{\sqrt{5}},~\sin\alpha=\dfrac{1}{\sqrt{5}}}$．

  2. 図のように書くことができ，

    三角関数の加法定理と平面図形の解答の図その１

    $ \text{X}'\left(\cos\dfrac{\pi}{3},~\sin\dfrac{\pi}{3}\right)$なので$\boldsymbol{ \text{X}'\left(\dfrac12,~\dfrac{\sqrt{3}}{2}\right)}$．

    $ \text{A}'\left(\sqrt{5}\cos\left(\alpha+\dfrac{\pi}{3}\right),~\sqrt{5}\sin\left(\alpha+\dfrac{\pi}{3}\right)\right)$であり，

    \begin{align} &\cos\left(\alpha+\dfrac{\pi}{3}\right)=\cos\alpha\cos\dfrac{\pi}{3}-\sin\alpha\sin\dfrac{\pi}{3}\\ &=\dfrac{2}{\sqrt{5}}\cdot\dfrac12 - \dfrac{1}{\sqrt{5}}\cdot\dfrac{\sqrt{3}}{2} =\dfrac{2-\sqrt{3}}{2\sqrt{5}}\\ &\sin\left(\alpha+\dfrac{\pi}{3}\right)=\sin\alpha\cos\dfrac{\pi}{3}+\cos\alpha\sin\dfrac{\pi}{3}\\ &=\dfrac{1}{\sqrt{5}}\cdot\dfrac12 + \dfrac{2}{\sqrt{5}}\cdot\dfrac{\sqrt{3}}{2} =\dfrac{1+2\sqrt{3}}{2\sqrt{5}} \end{align}

    ← 正弦と余弦の加法定理

    より，$\boldsymbol{ \text{A}'\left(\dfrac{2-\sqrt{3}}{2},~\dfrac{1+2\sqrt{3}}{2}\right)}$．

    ←$\cos\left(\alpha+\dfrac{\pi}{3}\right),~\sin\left(\alpha+\dfrac{\pi}{3}\right)$をそれぞれ$\sqrt{5}$倍した

正接の加法定理

正接の加法定理

正弦と余弦の加法定理から，次のような正接の加法定理を導くことができる．

\begin{align} \tan(\alpha+\beta)=\dfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta} \end{align} $\tag{2}\label{seisetunokahouteiri1}$

【証明】

\begin{align} &\tan(\alpha+\beta)=\dfrac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)}\\ &=\dfrac{\sin\alpha\cos\beta+\cos\alpha\sin\beta}{\cos\alpha\cos\beta-\sin\alpha\sin\beta}\\ &=\dfrac{\dfrac{\sin\alpha}{\cos\alpha}+\dfrac{\sin\beta}{\cos\beta}}{1-\dfrac{\sin\alpha}{\cos\alpha}\cdot\dfrac{\sin\beta}{\cos\beta}} \end{align}

←分母と分子を$\cos\alpha\cos\beta$で割った

\[=\dfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\]

暗記正接の加法定理の導出

上の$\eqref{seisetunokahouteiri1}$を利用して，次の等式を証明せよ．

\begin{align} \tan(\alpha-\beta)=\dfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta} \end{align}

$\eqref{seisetunokahouteiri1}$の$\beta$を$ − \beta$におきかえると

\begin{align} &\tan\{\alpha+(-\beta)\}=\dfrac{\tan\alpha+\tan(-\beta)}{1-\tan\alpha\tan(-\beta)}\\ \Leftrightarrow~&\tan(\alpha-\beta)=\dfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta} \end{align}

←$-\theta$ の三角比

正接の加法定理

\begin{align} &\tan(\alpha+\beta)=\dfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\\ &\tan(\alpha-\beta)=\dfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta} \end{align}

正接の加法定理

$0<\alpha<\dfrac{\pi}{2},~~0<\beta<\dfrac{\pi}{2}$で，$\tan\alpha=5,~\tan\beta=\dfrac{3}{2}$のとき，次の問いに答えよ．

  1. $\tan(\alpha+\beta),~\tan(\alpha-\beta)$の値を求めよ．
  2. $\alpha+\beta$の値を求めよ．

  1. 正接の加法定理より

    \begin{align} \tan(\alpha+\beta)&=\dfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\\ &=\dfrac{5+\dfrac{3}{2}}{1-5\cdot\dfrac{3}{2}}=\boldsymbol{-1}\\ \tan(\alpha-\beta)&=\dfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}\\ &=\dfrac{5-\dfrac{3}{2}}{1+5\cdot\dfrac{3}{2}}=\boldsymbol{\dfrac{7}{17}} \end{align}

  2. $0<\alpha+\beta<\pi$および，$\tan(\alpha+\beta)=-1$より，$\alpha+\beta=\boldsymbol{\dfrac{3}{4}\pi}$である．

2直線のなす角

2直線のなす角

正接の加法定理を利用すると，2直線のなす角の正接の値を求めることができる． そのことを次の例題で確認しよう．

2直線のなす角〜その1〜

直線$l:y=2x-1,m:y=\dfrac{1}{3}x+\dfrac{1}{3}$について，以下の問いに答えよ．

  1. 直線$l,m$が$x$軸の正の向きとなす角を$\alpha,\beta$とするとき，$\tan\alpha,\tan\beta$の値を求めよ． ただし，角は反時計回りを正の向きとする．

  2. 2直線$l,m$のなす鋭角を$\theta$とする．正接の加法定理を利用し$\theta$の値を求めよ．

無題
無題

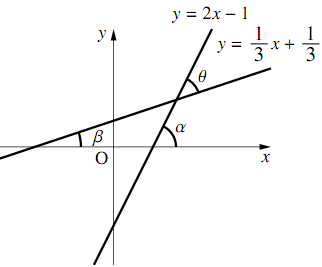
  1. 直線$l$と$m$の傾きはそれぞれ，$2,\dfrac{1}{3}$なので，

    $\tan\alpha=\boldsymbol{2},\tan\beta=\boldsymbol{\dfrac{1}{3}}$である．

  2. $\theta = \beta − \alpha$なので

    \begin{align} &\tan\theta\\ &=\tan(\alpha-\beta)\\ &=\dfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}\\ &=\dfrac{2-\dfrac{1}{3}}{1+2\cdot\dfrac{1}{3}}\\ &=1 \end{align}

    $0\leqq\theta\leqq\dfrac{\pi}{2}$より，$\theta=\boldsymbol{\dfrac{\pi}{4}}$となる．

以下では，交わる2直線$y=m_1x+n_1,y=m_2x+n_2$のなす鋭角$\theta$について，一般的に考えてみよう．

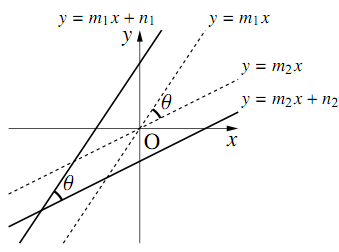
2直線のなす角の図その１

図のように，直線を平行移動しても2直線のなす角は変わらないので，$y=m_1x,y=m_2x$の場合について考えてゆけばよい．

直線$y=m_1 x,~y=m_2 x$が$x$軸の正の向きとなす，正の角をそれぞれ$\alpha,\beta~(\alpha>\beta)$とする．

正接の値は直線の傾きを表していたので，$\tan\alpha=m_1,~\tan\beta=m_2$である．

いま，正接の加法定理から

\begin{align} \tan(\alpha-\beta)&=\dfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}=\dfrac{m_1-m_2}{1+m_1m_2} \end{align}

と計算できる．

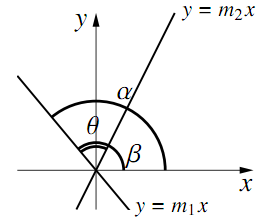
2直線のなす角の図その２

  1. $\dfrac{m_1-m_2}{1+m_1m_2}>0$,すなわち$0<\alpha-\beta <\dfrac{\pi}{2}$のとき

    \begin{align} \tan\theta=\tan(\alpha-\beta)=\dfrac{m_1-m_2}{1+m_1m_2}~(>0) \end{align}




    2直線のなす角の図その３

  2. $\dfrac{m_1-m_2}{1+m_1m_2}<0$,すなわち$\dfrac{\pi}{2}<\alpha-\beta<\pi$のとき

    \begin{align} \tan\theta&=\tan\left\{\pi-(\alpha-\beta)\right\}\\ &=-\tan(\alpha-\beta)\\ &=-\dfrac{m_1-m_2}{1+m_1m_2}~(>0) \end{align}

    いずれにしても，$\tan\theta > 0$なので，次のようにまとめられる．

2直線のなす角

無題

無題

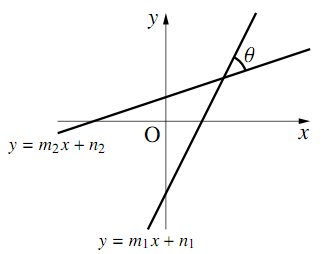
直交しない2直線

\begin{align} &y=m_1x+n_1~~~~~y=m_2x+n_2 \end{align}

のなす鋭角を$\theta$とすると

\begin{align} \tan\theta=\left|\dfrac{m_1-m_2}{1+m_1m_2}\right| \end{align}

と表すことができる．

2直線のなす鋭角〜その2〜

  1. 2直線$y=2x-1,~y=-x+3$なす角を$\theta$とするとき，$\tan\theta$の値を求めよ．

  2. 直線$y=2x+3$とのなす角が$\dfrac{\pi}{4}$である直線の傾き$m$を求めよ．

  1. それぞれ傾きは$2,~-1$なので

    \begin{align} \tan\theta =\left|\dfrac{2 -(-1)}{1+2\cdot (-1)}\right| =|-3| =\boldsymbol{3} \end{align}

  2. 傾きは$2,~m$である2直線のなす角が$\dfrac{\pi}{4}$なので

    \begin{align} \tan\dfrac{\pi}{4}=\left|\dfrac{2 -m}{1+2\cdot m}\right| \Leftrightarrow~ &1=\left|\dfrac{2-m}{2m+1}\right| \end{align}

    よって，$2m+1=2-m$または$2m+1=m-2$であればよいので， $\boldsymbol{m=\dfrac{1}{3},~-3}$．