三角関数の合成

三角関数の合成について

無題

無題

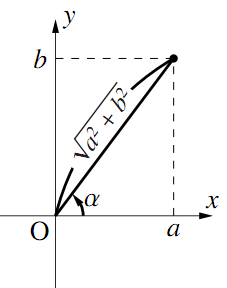
三角関数の合成について

$a\sin\theta + b\cos\theta$の形をしている式は，加法定理をもちいてより簡単な形に直すことができる．

図のように，$\sin\theta$の係数を$x$座標とし，$\cos\theta$の係数を$y$座標とする点$\text{P}(a,~b)$をとり， 線分$\text{OP}$が$x$軸の正の向きとなす，正の向きの角を$\alpha$とすると

\begin{align} \cos\alpha=\dfrac{a}{\sqrt{a^2+b^2}}~,~~\sin\alpha=\dfrac{b}{\sqrt{a^2+b^2}} \end{align} $\tag{1}\label{sankakukansuunogouseinituite1}$

だから

\[a\sin\theta + b\cos\theta\] \[=\sqrt{a^2+b^2}\left(\dfrac{a}{\sqrt{a^2+b^2}}\sin\theta\right.\] \[\qquad\qquad\qquad\left.+\dfrac{b}{\sqrt{a^2+b^2}}\cos\theta\right)\]

←$\sqrt{a^2+b^2}$で式全体をくくった

\[=\sqrt{a^2+b^2}(\cos\alpha\sin\theta+\sin\alpha\cos\theta)\]

←$\eqref{sankakukansuunogouseinituite1}$を使った

\[=\sqrt{a^2+b^2}\sin(\theta+\alpha)\]

←加法定理を使った

この変形のことを，三角関数の合成(combination of trigonometric function) という．

三角関数の合成

無題

無題

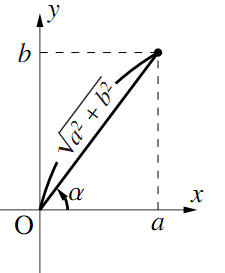
$a\sin\theta + b\cos\theta$は

\begin{align} \cos\alpha=\dfrac{a}{\sqrt{a^2+b^2}}~,~~\sin\alpha=\dfrac{b}{\sqrt{a^2+b^2}} \end{align}

を満たす$\alpha$をもちいて

\begin{align} a\sin\theta+b\cos\theta=\sqrt{a^2+b^2}\sin(\theta+\alpha) \end{align}

と変形できる．

三角関数の合成

次の三角関数を合成して，$A\sin(\theta+\alpha)$の形に変形せよ．$ \alpha$の値が求められるときには求めよ(ただし，$0\leqq\alpha<2\pi$とする)．

  1. $\sin\theta +\cos\theta$
  2. $-\sin\theta +\sqrt{3}\cos\theta$
  3. $3\sin\theta -4\cos\theta$

  1. 三角関数の合成の解答の図その１
    \begin{align} &\sin\theta+\cos\theta\\ &=\sqrt{1^2+1^2}\left(\dfrac{1}{\sqrt{2}}\sin\theta+\dfrac{1}{\sqrt{2}}\cos\theta\right)\\ &=\sqrt{2}\left(\cos\dfrac{\pi}{4}\sin\theta+\sin\dfrac{\pi}{4}\cos\theta\right)\\ &=\boldsymbol{\sqrt{2}\sin\left(\theta+\dfrac{\pi}{4}\right)} \end{align}




  2. 三角関数の合成の解答の図その２
    \begin{align} &-\sin\theta+\sqrt{3}\cos\theta\\ &=\sqrt{(-1)^2+\sqrt{3}^2}\left(\dfrac{-1}{2}\sin\theta+\dfrac{\sqrt{3}}{2}\cos\theta\right)\\ &=2\left(\cos\dfrac{2\pi}{3}\sin\theta+\sin\dfrac{2\pi}{3}\cos\theta\right)\\ &=\boldsymbol{2\sin\left(\theta+\dfrac{2\pi}{3}\right)} \end{align}




  3. 三角関数の合成の解答の図その３
    \begin{align} &3\sin\theta-4\cos\theta\\ &=\sqrt{3^2+(-4)^2}\left(\dfrac{3}{5}\sin\theta-\dfrac{4}{5}\cos\theta\right)\\ &=5\left(\cos\alpha\sin\theta+\sin\alpha\cos\theta\right)\\ &=\boldsymbol{5\sin\left(\theta +\alpha \right)} \end{align}

ただし，$\alpha$は図のような角度である．