外心の定理
外心の定理
外心
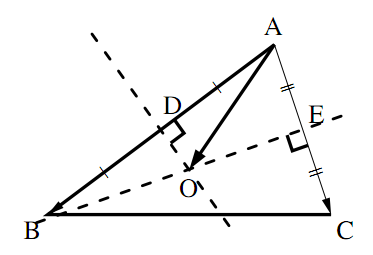
どんな三角形でも,3辺の垂直二等分線は1点で交わる.
証明
無題
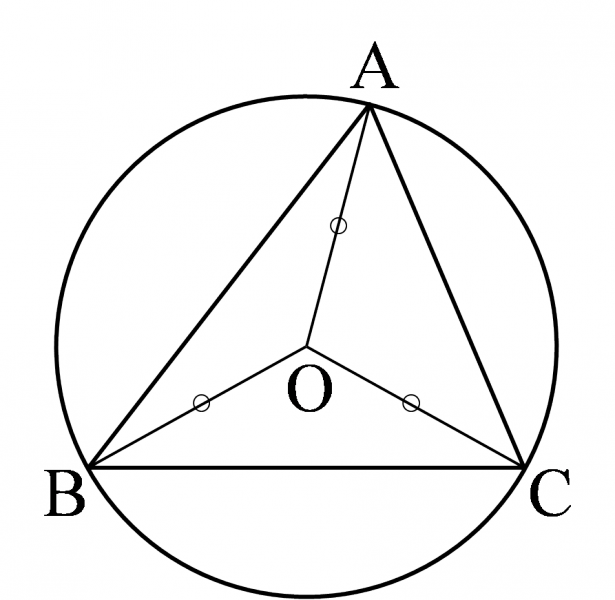
$\triangle{\mathrm{ABC}}$ において,3辺の垂直二等分線が交わる点を $\mathrm{O}$ とすると,上の証明により,点 $\mathrm{O}$ は $\triangle{\mathrm{ABC}}$ の3つの頂点から等距離にある.よって,この点 $\mathrm{O}$ を中心とする半径 $\mathrm{OA}$ の円は, $\triangle{\mathrm{ABC}}$ の3つの頂点を通る.
この円を, $\triangle{\mathrm{ABC}}$ の外接円といい,点 $\mathrm{O}$ を $\triangle{\mathrm{ABC}}$ の外心という.
外心
無題

次の図において,次の角の大きさを求めよ.ただし,点 $\text{O}$ は$\triangle{\mathrm{ABC}}$ の外心とする.
- $\angle{\text{ABO}}$
- $\angle{\text{BOC}}$
$\triangle{\mathrm{OAB}},\triangle{\mathrm{OBC}},\triangle{\mathrm{OCA}}$ は二等辺三角形である.
- $\angle{\mathrm{OAC}}=\angle{\mathrm{OCA}}=20^\circ$ より,
- $\triangle{\mathrm{ABC}}$ において,
$\angle{\mathrm{ABO}}=\angle{\mathrm{BAO}}=80^\circ-20^\circ=\boldsymbol{60^\circ}$
\begin{align} &20^\circ+80^\circ+60^\circ+\angle{\text{OBC}}+\angle{\text{OCB}}\\ &=180^\circ \end{align} よって,
$\angle{\text{OBC}}+\angle{\text{OCB}}=20^\circ$ だから, $\triangle{\mathrm{OBC}}$ において,
$\angle{\text{BOC}}=180^\circ-20^\circ=\boldsymbol{160^\circ}$