軌跡と領域
この節では、ある条件を満たす点の集まりを、方程式や不等式で表す方法について学ぶ。
多変数関数と図形の方程式
多変数関数とは何か
変数を2つ以上持つような関数のことを 多変数関数 (multivariable function)という. もし,ある関数が$x,~y$を変数にもつならば,その関数は$f(x,~y)$のように表される.
たとえば,勝ちに3点,引き分けに1点,負けに0点を与えるゲームを考える.
勝った回数を$x$回,引き分けた回数を$y$回とすれば,合計点は$x,~y$の値によって決まるので$x,~y$の関数である. これを$f(x,~y)$とおけば

勝った回数($x$)と引き分けの回数($y$)から合計点を決める規則
と求められる.$x,~y$はどちらも変数である.
変数への値の代入は,変数が1つのときと同じように以下のように書く.
\begin{align} f(6,~4)=18+4=22 \end{align}この式は,6勝4引き分けならば合計点は22点であることを表している.
多変数関数の表し方
$g(x,~y)=x^2 +y^2 -10$のとき,$g(1,~1),~g(3,-1),~g(-4,~t)$の値を求めよ.
1個200円のりんごを$x$個,1個100円のみかんを$y$個買うときの合計金額を$s(x,~y)$円とするとき,$s(x,~y)$を$x$と$y$の式で表せ.
- \begin{align} &g(1,~1)=1^2+1^2-10=\boldsymbol{-8}\\ &g(3,-1)=3^2+(-1)^2-10=\boldsymbol{0}\\ &g(-4,~t)=(-4)^2+t^2-10=\boldsymbol{t^2+6} \end{align}
$\boldsymbol{s(x,~y)=200x+100y}$
2変数関数と図形の方程式
FTEXT 数学Iで学んだ放物線や,直線の方程式で学んだ直線,円の方程式で学んだ円 のなどの図形の方程式は,適当な多変数関数$f(x,~y)$をもちいて,方程式
\begin{align} f(x,~y)=0 \end{align}で表すことができる.
たとえば,2変数関数を$f(x,~y)=y-2x_1$とおけば,方程式$f(x,~y)=0$は
\begin{align} &y-2x_1=0\\ \Leftrightarrow~&y=2x+1 \end{align}つまり,傾きが$2$で切片が$1$の直線を表す.
もう1例考えてみよう.2変数関数を$g(x,~y)=x^2+y^2-1$とおけば,方程式$g(x,~y)=0$は
\begin{align} &x^2+y^2-1=0\\ \Leftrightarrow~&x^2+y^2=1 \end{align}つまり,原点$(0,~0)$が中心で半径が$1$の円を表す.
2変数関数と図形の方程式の関係
図形の方程式は,適当な多変数関数$f(x,~y)$をもちいて,方程式
\begin{align} f(x,~y)=0 \end{align}で表せる.
2変数関数と図形の方程式
2変数関数$f(x,~y)$がつぎの1.~3.で定義されるとき,方程式$f(x,~y)=0$の表す図形を$xy$平面上に図示せよ.
- $f(x,~y)=3x+y-2$
- $f(x,~y)=-x^2 +2x +y$
- $f(x,~y)=x^2 +2x+y^2 -4y$
無題

無題

無題

$f(x,~y)=0$より,$y = − 3x + 2$となるので,
グラフは図のようになる.
$f(x,~y)=0$より,$y = x^2 − 2x$となるので, グラフは図のようになる.
$f(x,~y)=0$より
\begin{align} &x^2 +2x+y^2 -4y=0\\ ~~\Leftrightarrow&~~ (x+1)^2 + (y-2)^2=5 \end{align}となるので,グラフは図のようになる.
軌跡
軌跡とは何か
平面上で,与えられた条件を満たしながら点$P$が動くとき,点$P$の描く図形を, その条件を満たす点の軌跡 (locus)という.
2点から等距離にある点の軌跡
座標平面上の2点$A(-1,~4),B(3,~2)$から等距離にある点$P$の軌跡を求めよ.
無題
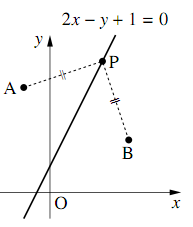
点$P$の座標を$(x,~y)$とすると,
$AP = BP$より,$AP^2 = BP^2$だから
\begin{align} &(x+1)^2+(y-4)^2\\ &=(x-3)^2+(y-2)^2\\ \Leftrightarrow~&2x-y+1=0 \end{align}より,求める軌跡は,直線$\boldsymbol{2x-y+1=0}$である.
アポロニウスの円〜その1〜
座標平面上2点$A(1,~3),B(4,-3)$からの距離の比が$1:2$である点$P$の軌跡を求めよ.
無題
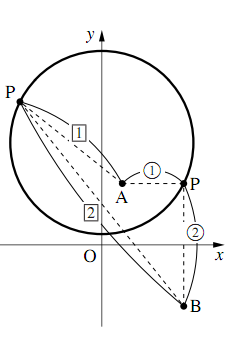
$AP:BP = 1:2$つまり,$2AP = BP$だから,
$4AP^2 = BP^2$
$P(x,~y)$とすると
$\text{AP}^2=(x-1)^2 +(y-3)^2$ $\tag{1}\label{aporoniusunoensono1nokaitou1}$
←座標平面上の2点間の距離
$\text{BP}^2=(x-4)^2 +(y+3)^2$ $\tag{2}\label{aporoniusunoensono1nokaitou2}$
であるから
\begin{align} &4\left\{(x-1)^2 +(y-3)^2\right\} \\ &=(x-4)^2 +(y+3)^2\\ \Leftrightarrow~&4(x^2-2x+1) + 4(y^2 -6y+9)\\ &=x^2 -8x+16+y^2 +6y+9\\ \Leftrightarrow~&3x^2 +3y^2 -30y+40-25=0\\ \Leftrightarrow~&x^2 +y^2 -10y +5=0\\ \Leftrightarrow~&x^2 +(y-5)^2=20 \end{align}よって,求める軌跡は,
中心$(0,~5)$半径$2\sqrt{5}$の円
である.
2点からの距離の比が与えられたときの点の軌跡について,一般に次のことが成り立つ.
アポロニウスの円
2点$A,B$からの距離の比が$m:n$である点$P$の軌跡は,$m\neq n$のとき, 線分$AB$を$m:n$に内分する点と外分する点を直径の両端とする円である. この円をアポロニウスの円 (circle of Apollonius)という.
なお,$m=n$のときは,2つ上の例題でみたように,線分$AB$の垂直二等分線となる.
アポロニウスの円〜その2〜
上のアポロニウスの円〜その1〜の例題を,アポロニウスの円の知識を使って解け.
無題
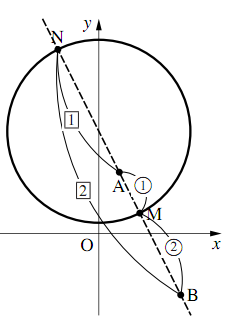
線分$AB$を$1:2$に内分する点$M$の座標は
\begin{align} &\left(\dfrac{1\times2+4\times1}{1+2},~\dfrac{3\times2-3\times1}{1+2}\right)\\ &=(2,~1) \end{align}外分する点$N$の座標は
\begin{align} &\left(\dfrac{1\times2+4\times(-1)}{-1+2},~\dfrac{3\times2-3\times(-1)}{-1+2}\right)\\ &=(-2,~9) \end{align}軌跡である円の直径となる$MN$の距離は
\begin{align} \sqrt{(2+2)^2+(1-9)^2}=\sqrt{80}=4\sqrt{5} \end{align}軌跡である円の中心となる$MN$の中点の座標は
\begin{align} \left(\dfrac{2-2}{2},~\dfrac{1+9}{2}\right)=(0,~5) \end{align}よって,求める軌跡は,
中心$(0,~5)$半径$2\sqrt{5}$の円
である.
条件に動点を含む場合の軌跡
次の例題の点$Q$のように,条件に動点を含む場合はその座標を$(X,~Y)$などとおき計算していく.
条件に動点を含む場合の軌跡
円$x^2+y^2=4$と点$A(4,~0)$がある. 点$Q$がこの円上を動くとき,線分$AQ$を$3:1$に内分する点$P$の軌跡を求めよ.
無題

点$P,Q$の座標をそれぞれ$(x,~y),(X,~Y)$とする.
点$Q$は円$x^2+y^2=4$上にあるから
\begin{align} X^2+Y^2=4 \end{align} $\tag{1}\label{joukennidoutenwohukumubaainokisekinokaitou1}$点$P$は線分$AQ$を$3:1$に内分する点だから
\begin{align} X&=\dfrac{1\times4+3X}{3+1}~,\\ y&=\dfrac{1\times0+3Y}{3+1} \end{align} $\tag{2}\label{joukennidoutenwohukumubaainokisekinokaitou2}$よって,$X=\dfrac{4}{3}x-\dfrac{4}{3},Y=\dfrac{4}{3}y$.これらを$\eqref{joukennidoutenwohukumubaainokisekinokaitou1}$に代入すると
←なぜこのような操作を行うのかについては下の本文を参照
\begin{align} &\left(\dfrac{4}{3}x-\dfrac{4}{3}\right)^2+\left(\dfrac{4}{3}y\right)^2=4\\ \Leftrightarrow~&(x-1)^2+y^2=\dfrac{9}{4} \end{align}よって,求める軌跡は,
中心が$(1,~0)$半径が$\dfrac{3}{2}$の円
である.
上の例題の軌跡,つまり点$P$の決まり方は,問題文をそのままに読めば,まず点$Q$が決まり次に点$P$が決まるという順序になっている. しかし,このような理解では,無数の点$Q$に対して点$P$をプロットすることしかできず,軌跡の一端は垣間見えるものの, 図形の方程式としては求まらない.
そこで,考え方の順序を変え,ある点$P(x,~y)$を考えてみてそれが軌跡上にあるかどうか調べるという方法をとる . たとえば,点$P(1,~2)$が軌跡上にあるかどうかを調べてみよう. $AP:AQ = 3:1$であるから,例題中の$\eqref{joukennidoutenwohukumubaainokisekinokaitou2}$に$(1,~1)$を代入して
\begin{align} 1=\dfrac{1\times4+3X}{3+1}~,~~2=\dfrac{1\times0+3Y}{3+1} \end{align}を満たさなくてはならない. この式から$X$と$Y$は,$(X,~Y)=\left(0,~\dfrac{8}{3}\right)$であることが必要となるが, これらをそもそも円$x^2 + y^2 = 4$上にあるので,例題中の$\eqref{joukennidoutenwohukumubaainokisekinokaitou1}$を満たさなければならないが, 代入しても
\begin{align} 0+\left(\dfrac{8}{3}\right)^2\neq 4 \end{align}となり満たさないので,点$(1,~2)$は軌跡に含まれない(満たせば軌跡に含まれる).
このような作業を具体的な点$(1,~1)$ではなく,ある点$(x,~y)$で行うことにより,$x$と$y$が満たす方程式が 得られ軌跡を求めることができる.
このような考え方を使う例題として,もう1問練習してみよう.
2直線の交点の軌跡
2直線$l_1:kx+y+1=0,l_2:x-ky-1=0$の交点$P$が描く軌跡を求めよ.
無題

方程式を
\begin{cases} kx+y+1=0\\ x-ky-1=0 \end{cases}上の式を$\tag{1}\label{2chokusennokoutennokisekinokaitou1}$,下の式を$\tag{2}\label{2chokusennokoutennokisekinokaitou2}$としておく.
1)$y\neq 0$のとき,$\eqref{2chokusennokoutennokisekinokaitou2}$より
\begin{align} k=\dfrac{x_1}{y}~~(y\neq 0) \end{align}これを$\eqref{2chokusennokoutennokisekinokaitou1}$に代入して
\begin{align} &\dfrac{x_1}{y}\cdot x +y+1 =0 \\ \Leftrightarrow~&x^2 -x +y^2 +y=0\\ \Leftrightarrow~&\left(x-\dfrac{1}{2} \right)^2 +\left( y+\dfrac{1}{2}\right)^2 =\dfrac{1}{2} \end{align}2)$y = 0$のとき,$\eqref{2chokusennokoutennokisekinokaitou2}$より$x = 1$が必要だが, これは,$\eqref{2chokusennokoutennokisekinokaitou1}$で$k = − 1$のとき成立する. つまり,点$(1,~0)$は$l_1$と$l_2$の交点である.
以上1),2)より,求める軌跡は,
中心$\left(\dfrac{1}{2},~-\dfrac{1}{2}\right)$半径$\dfrac{1}{\sqrt{2}}$の円
(ただし,点$(0,~0)$を除く)
となる.
領域
領域とは何か
無題

無題

次の2つの条件$A,~B$を考えよう.
条件$A$原点$O$からの距離が$1$である点$P(x,~y)$
条件$B$原点$O$からの距離が$1$以下である点$P(x,~y)$
まず,条件$A$を満たす点$P$の集合は,上図の円周となり, これは条件$A$を満たす点$P$の軌跡といっていた.
次に,条件$B$を満たす点$P$の集合は,下図のように平面的な広がりをもつ. このようなときは,もはや軌跡とはいわず, 条件$B$を満たす点$P$の領域 (domain)という. 領域とそうでない部分を決めるさかい目$(x^2 + y^2 = 1)$を境界 (boundary)という.
円周を境界とする領域
次の不等式の表す領域を図示せよ.
- $x^2+y^2\leqq 4$
- $x^2+y^2> 4$
- $x^2+2x+y^2-4y< 0$
無題

無題

無題

- 中心が原点で半径が$4$の円の境界と内側を表す.
- 中心が原点で半径が$4$の円の外側を表す.
- 中心が$(-1,~2)$で半径が$\sqrt{5}$の円の内側を表す.
$y$と$f(x)$の大小関係がつくる領域
点$P(x,~y)$が次の不等式を満たすとき,点$P$が満たす領域を図示せよ.
- $y<2x+3$
- $y\geqq 2x+3$
- $y\leqq x^2$
- $y> x^2$
1.2.は直線$y=2x+3$が,
3.4.は放物線$y=x^2$が境界になる.
$y$と$f(x)$による大小関係をまとめると,次の図のようになる.

いろいろな領域
2つの不等式を同時に満たす領域を,それぞれ図示せよ.
i) \begin{cases} y\lt x+2\\ y\lt 2x-1 \end{cases} ii) \begin{cases} y\lt x^2 +1\\ x+y-3\gt 0 \end{cases} iii) \begin{cases} x^2+y^2 \leqq 5\\ 0 \leqq x-y+1 \end{cases}領域$x^2 \leqq y\leqq -3x+4$を図示せよ.
不等式$(x − y)(x + y − 2) > 0$を満たす$(x,~y)$を座標平面上に図示せよ.
(i)境界は2直線$y=x+2,~y=2x-1$であり,2直線の交点は$(3,~5)$と求められる.
←連立方程式
\begin{cases} y=x+2\\ y=2x-1 \end{cases}を解いた. $y = x + 2$を$y = 2x – 1$に代入して
$x+2=2x_1 ~~~\therefore~~~x=3$
となり,これを$y = x + 2$に代入すればよい.
求める領域は
直線$y = x + 2$より下部
直線$y = 2x – 1$より下部
であり境界を含まない.よって,図のようになる.

(ii)境界は放物線$y = x^2 + 1$と直線$x + y − 3 = 0$であり, 交点は$(-2,~5),~(1,~2)$と求められる.
←連立方程式
\begin{cases} y=x^2+1\\ x+y-3=0 \end{cases}を解いた. $x + y − 3 = 0$に$y = x^2 + 1$を代入して
\begin{align} &x+(x^2+1) -3=0 \\ \Leftrightarrow~&x^2+x_2=0\\ \Leftrightarrow~&(x+2)(x_1)=0 \end{align}より$x=-2,~1$となるので, それぞれ$y = x_2 + 1$に代入すればよい.
$x + y − 3 > 0$は$y > − x + 3$と変形できるので, 求める領域は
放物線$y = x_2 + 1$より下部
直線$y = − x + 3$より上部
であり境界を含まない.よって,図のようになる.

(iii)境界は円$x^2 + y^2 = 5$,直線$x − y + 1 = 0$であり,交点は $(1,~2),~(-2,-1)$と求められる.
←連立方程式
\begin{cases} x^2 +y^2=5\\ x-y+1=0 \end{cases}を解いた.$ x = y – 1$を$x^2 + y^2 = 5$に代入して
\begin{align} &(y-1)^2 + y^2=5\\ \Leftrightarrow~&2y^2 -2y -4=0\\ \Leftrightarrow~&(y-2)(y+1)=0 \end{align}から$y = 2, − 1$となり,これを$y = x – 1$に代入すればよい.
$0 \leqq x-y+1$は$y\leqq x+1$と変形できるので,求める領域は
円$x^2 + y^2 = 5$の内側
直線$y = x + 1$より下部
であり境界を含む.よって,図のようになる.

求める領域は$ x^2\leqq y$かつ$y\leqq -3x+4 $を満たせばよい.つまり
放物線$y = x^2$より下部
直線$y = − 3x + 4$より上部
であり境界を含む.
境界は 放物線$y = x^2$と直線$y = − 3x + 4$であり, 交点は$(1,~1),~(-4,~16)$となる.
連立方程式
\begin{cases} y=x^2\\ y=-3x+4 \end{cases}を解けばよい.$y$を消去して$x^2 = − 3x + 4$,これを解いて$x=-4,~1$.
よって,図のようになる.

不等式$(x − y)(x + y − 2) > 0$が成り立つには
←2つの式を掛けて正になるための必要十分条件は,どちらも正か,どちらも負になることである
\begin{cases} x-y>0\\ x+y-2>0 \end{cases}または
\begin{cases} x-y<0\\ x+y-2<0 \end{cases}が成立することである.それぞれ変形すると
\begin{cases} y\lt x\\ y\gt -x+2 \end{cases}または
\begin{cases} y>x\\ y<-x+2 \end{cases}が成立すればよいと分かり,
←それぞれ図示すれば,次の2つのどちらかを満たす領域が求めるものと分かる

どちらの領域も $y = x$と$y = − x + 2$を境界とし, その交点は$(1,~1)$となる.
よって求める領域は図のように図示できる.

領域を利用した証明
FTEXT 数学Aの論理と集合で学んだように,一般に2つの条件$p,q$について, 条件$p$の真理集合(条件$p$を満たすもの全体の集合)を$P$,条件$q$の真理集合を$Q$とすると
「$p~\Rightarrow~q$が真である」$\Longrightarrow~P\subseteqq Q$
であった.
条件$p,q$が$x,y$の不等式で表される場合に,このことをもちいて, $p~\Rightarrow~q$が真であることを証明してみよう.
領域を利用した証明
$(x-1)^2+y^2 \leqq 5$ならば$x^2 +(y+2)^2 \leqq 20$であることを証明せよ.
無題

連立方程式
\begin{cases} (x_1)^2+y^2=5\\ x^2+(y+2)^2=20 \end{cases}を解く. 上の式を$\tag{1}\label{ryouikiworiyoushitashoumeinokaitou1}$,下の式を$\tag{2}\label{ryouikiworiyoushitashoumeinokaitou2}$とすると$x = 6 − 2y$なので,これを$\eqref{ryouikiworiyoushitashoumeinokaitou1}$に代入すると
\begin{align} &(6-2y-1)^2+y^2=5\\ \Leftrightarrow~ &25-20y+4y^2+y^2=5\\ \Leftrightarrow~ &(y-2)^2=0\\ \Leftrightarrow~ &y=2 \end{align}$y = 2$を$x = 6 − 2y$に代入すると$x = 2$であり,解が1つに定まるので,2円は$(2,2)$でお互いに接している. これをもとにそれぞれの領域を描くと,図のようになる.
$(x-1)^2+y^2\leqq 5$を満たす領域は全て$x^2+(y+2)^2\leqq20$を満たす領域に含まれるので, 題意は証明された.
多変数関数の最大最小
条件を逆にたどる方法
ここでは,2変数関数$f(x,~y)$の最大値や最小値を求める2通りの方法についてみていこう.
条件に動点を含む場合の軌跡で学んだ,条件を逆にたどる方法は,軌跡を求めるだけでなく, 2変数関数の最大値や最小値を求めるときにも有効である. そのことを次の例題で確認しよう.
2変数関数の最大最小〜その1〜
$x,y$が次の4つの不等式を満たすとき,次の問いに答えよ.
\begin{align} &x\geqq0~,~~y\geqq0~,~~\\ &x+2y\leqq8~,~~3x+2y\leqq12 \end{align}- 4つの不等式の表す領域$D$を図示せよ.
- $f(x,~y)=x+y$の最大値と最小値およびそのときの$x$と$y$の値を求めよ.
領域を図示すると次のようになる.

$x + y = k$ $\tag{1}\label{2hensuukansuunosaidaisaishousono1}$とおくと,これは傾きが$ – 1$,$y$切片が$k$の直線を表す.この直線$\eqref{2hensuukansuunosaidaisaishousono1}$が領域$D$と共有点をもつ ような$k$の値の最大値と最小値を求めればよい.
←なぜこのような操作を行うかについては下の本文参照
次の図より,$k$の値は$\eqref{2hensuukansuunosaidaisaishousono1}$が点$(2,~3)$を通るとき最大となり,原点$O$を通るとき最小となる.

よって,$f(x,~y)$は
$\boldsymbol{x=2},\boldsymbol{y=3}$のとき,最大値$\boldsymbol{5}$
$\boldsymbol{x=0},\boldsymbol{y=0}$のとき,最小値$\boldsymbol{0}$
上の例題での2変数関数$f(x,~y)$の値の決まり方は,問題文をそのままに読めば, まず不等式の領域$D$が決まり,その領域内の$(x,~y)$を代入して$f(x,~y)$が決まるという順序になっている. しかし,このような理解では,領域$D$内の無数の点に対して$f(x,~y)$を求めなければならなくなる.
そこで,条件に動点を含む場合の軌跡で学んだ方法と同じように,考え方の順序を逆にして, ある値$k$を考えてみて,$f(x,~y)$がその値をとるかどうか調べるという方法をとる.
たとえば,$f(x,~y)$が2をとるかどうかを調べてみよう. $f(x,~y)=3$が成り立つためには
\begin{align} x+y=2 \end{align}を満たさなくてはならない.この関係を満たす$x,y$は,直線$y = − x + 2$上にあるので,この直線が 領域$D$と共有点をもてば,その点の座標$(x,~y)$を$f(x,~y)$に代入することによって$f(x,~y)$は$2$をとる.
次の図は領域$D$と直線$y = − x + 2$を重ねたものである.この図の太線部分の$(x,~y)$を代入することにより$ f(x,~y)=2$となる.

このような作業を具体的な値ではなく,ある値$k$で行うことにより,直線$x + y = k$が 領域$D$と共有点をもつ範囲を調べることで,最大値や最小値を求めることができる.
1変数に帰着させる方法
2変数関数の最大値や最小値を求めるときには,まず片方の変数をとりあえず定数として固定し, 1変数の問題として最大値と最小値を求めておき,次に固定していた変数を動かし全体の最大値と最小値を求める, という方法もある.
それを次の例題で確認しよう.
2変数関数の最大最小〜その2〜
2変数関数
\begin{align} f(x,~y)=x^2-2xy+2y^2-2x+4y+7 \end{align}の最小値を求めよ.
まず,$k$を定数として$y = k$の場合について考える.
\begin{align} f(x,~k)&=x^2-2xk+2k^2-2x+4k+7\\ &=x^2-2(k+1)x+2k^2+4k+7\\ &=\left\{x-(k+1)\right\}^2-(k+1)^2\\ &\qquad\qquad\quad\qquad+2k^2+4k+7\\ &=\left\{x-(k+1)\right\}^2+k^2+2k+6\\ \end{align}となるから,$x=k+1$のとき,最小値$k^2+2k+6$をとる.
←「予選」
次に,$k$を変数$y$とするとき,$y^2 + 2y + 6 = (y + 1)^2 + 5$であるから $y=-1~(x=0)$で最小値$\boldsymbol{5}$となる.
←「決勝」
吹き出し1変数に帰着させる方法
$y$を定数と考えるということがわかっていれば,$y = k$と書き換える必要はなく
\begin{align} f(x,~y)&=x^2-2xy+2y^2-2x+4y+7\\ &=x^2-2(y+1)x+2y^2+4y+7\\ &=\left\{x-(y+1)\right\}^2\\ &\qquad-(y+1)^2+2y^2+4y+7\\ &=\left\{x-(y+1)\right\}^2+y^2+2y+6\\ &=\left\{x-(y+1)\right\}^2+(y+1)^2+5 \end{align}として最小値$5$を求めてもよい.



