累乗と累乗根

同じ数$x$を何回か掛けて$a$という値になるとき、$x$を「$a$の累乗根」という。ここでは、累乗根に関する計算法則を学ぶ。

累乗と指数法則

累乗と指数法則について

累乗と指数法則について

\FTEXT 数学Iで学んだように， 数$a$の$n$個の積 $ \begin{array}{c} n個 \\ \overbrace{a\times a\times\cdots\times a}^{} \end{array} $ を $a^n$と書き，「$a$の$n$乗」と読む．つまり

\[ \begin{array}{c} \underbrace{a\times a\times\cdots\times a}_{}=a^n \\ n個 \qquad \end{array} \]

である． このとき，$a$の右上に乗っている数$n$のことを$a^n$の指数（index number）という． $a^1 = a$とし，特に，$a^2$のことを$a$の平方（square）， $a^3$のことを$a$の立方（cube）という． また，$a，a^2，a^3，\cdots$を総称して$a$の累乗（power）という．

累乗に関して

  1. $a^2\times a^4= \begin{array}{c} \\ \\ (\underbrace{a\times a}_{}) \\ 2個 \end{array} \times \begin{array}{c} \\ \\ (\underbrace{a\times a\times a\times a}_{}) \\ 4個 \end{array} $
    $ =a^6~(=a^{2+4})$
  2. $(a^2)^4= \begin{array}{c} \\ \\ (\underbrace{a\times a}_{}) \\ 2個 \end{array} \begin{array}{c} \\ \\ (\underbrace{a\times a}_{}) \\ 2個 \end{array} \begin{array}{c} \\ \\ (\underbrace{a\times a}_{}) \\ 2個 \end{array} \begin{array}{c} \\ \\ (\underbrace{a\times a}_{}) \\ 2個 \end{array} $
    $ =a^8~(=a^{2\times4})$
  3. $(a\times b)^4$
    $ =(a\times b)\times(a\times b)\times(a\times b)\times(a\times b)$
    $ =a^4\times b^4$

などの例からわかるように，一般に次のような指数法則（law of exponents）が成り立つ．

指数法則

$x，y$が自然数のとき，次の関係が成り立つ．

  1. $a^xa^y=a^{x+y}$
  2. $({a}^{x})^{y}=a^{xy}$
  3. $ (ab)^x=a^xb^x$

累乗根

累乗根とは何か

累乗根とは何か

$2$乗して$3$になる数を$3$の平方根とよび$\pm\sqrt{3}$と表していた． ここでは，$2$乗だけに限らず，$3$乗，$4$乗，$\cdots$の場合についても拡張して考えてみよう．

$n$乗根の定義

$n$を自然数とする．$n$乗すると$a$になる数，つまり

\begin{align} x^n=a \end{align}

となる$x$の値を，$a$の$n$乗根（$n$th root）という．

たとえば，$2^3 = 8$なので，$2$は$8$の$3$乗根である． また，$2^4 = 16$であり$( − 2)^4 = 16$であるから， $− 2$と$2$はともに$16$の$4$乗根である．

特に，$2$乗根を平方根（square root）， $3$乗根を立方根（cubic root）という． また，$2$乗根，$3$乗根，$4$乗根，$\cdots$を総称して， 累乗根（radical root）という．

$a$の$n$乗根の表し方

$0$でない実数$a$の$n$乗根は，次のようになる．

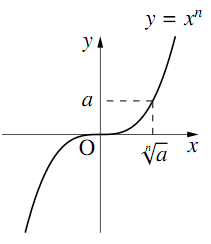
aのn乗根の表し方の図その１

  1. $n$が奇数のとき

    $y = x^n$のグラフは図のようになるので（たとえば$n = 3$として$x$を変化させて計算してみるとよい），$a$の正負に関係なく，$a$の$n$乗根はただ1つだけ存在し，それを$\sqrt[n]{a}$（$n$乗根$a$と読む） と表す．

    $\sqrt[n]{a}$の正負は$a$の正負と同じになる．

    たとえば，$2^3 = 8$であるから，$\sqrt[3]{8}=2$である．

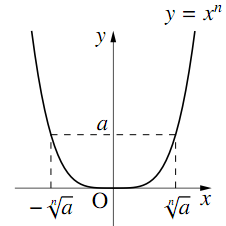
    2. aのn乗根の表し方の図その２

  2. $n$が偶数のとき

    $y = x^n$のグラフは図のようになるので（たとえば$n = 4$として$x$を変化させて計算してみるとよい）， $a$が正のときに正と負の2つの$n$乗根が存在する． そのうち正のものを$\sqrt[n]{a}$と表し，負のものを$-\sqrt[n]{a}$と表す．

    たとえば，$2^4 = 16，( − 2)^4 = 16$であるから，

    $\sqrt[4]{16}=2，-\sqrt[4]{16}=-2$である．

    なお，$a$が負のときには，$a$の$n$乗根は存在しない．

    $0$は何乗しても$0$なので，$0$の累乗根はすべて$0$である．つまり，$\sqrt[n]{0}=0$である．

累乗根の値を求める-その1-

次の値を求めよ．

  1. $\sqrt[3]{-27}$
  2. $-\sqrt[4]{81}$
  3. $\sqrt[6]{0.000001}$
  4. $\sqrt[3]{0.125}$

    $\blacktriangleleft$

    \begin{align} &x^3=-27\\ &\Leftrightarrow~x^3+27=0\\ &\begin{array}{c} \Leftrightarrow~(x+3)\underbrace{(x^2+3x+9)}_{}=0\\ \qquad\quad正 \end{array} \end{align}

  1. $− 27$の$3$乗根，つまり$x^3 = − 27$となる$x$は $− 3$である．

    よって

    \begin{align} \sqrt[3]{-27}=\boldsymbol{-3} \end{align}

    2. $\blacktriangleleft$

    \begin{align}&x^4=81\\ &\Leftrightarrow~x^4-81=\\ &\Leftrightarrow~(x^2-9)(x^2+9)=0\\ &\begin{array}{c} \Leftrightarrow~(x-3)(x+3)\underbrace{(x^2+9)}_{}=0\\ \qquad\qquad\qquad正 \end{array} \end{align}

  2. $81$の$4$乗根， つまり$x^4 = 81$となる$x$は $− 3$と$3$である． $-\sqrt[4]{81}$は負の方を表すから

    \begin{align} -\sqrt[4]{81}=\boldsymbol{-3} \end{align} $\blacktriangleleft$正の方の$\sqrt[4]{81}=3$にマイナスがつき $− 3$となると考えても良い

    3. $\blacktriangleleft$

    \begin{align}&x^6=0.000001\\ &\Leftrightarrow~x^6-0.000001=0\\ &\Leftrightarrow~(x^3-0.001)(x^3+0.001)=0\\ &\begin{array}{c} (x-0.1)\underbrace{(x^2+0.1x+0.01)}_{}=0\\ \qquad正 \end{array} \end{align}

    または

    \begin{align} \begin{array}{c} (x+0.1)\underbrace{(x^2-0.1x+0.01)}_{}=0\\ \qquad正 \end{array} \end{align}

  3. $0.000001$の$6$乗根， つまり$x^6 = 0.000001$となる$x$は $− 0.1$と$0.1$である． $ \sqrt[6]{0.000001}$は正の方を表すから

    \begin{align} \sqrt[6]{0.000001}=\boldsymbol{0.1} \end{align}

    4. $\blacktriangleleft$

    \begin{align} &x^3=0.125\\ &\Leftrightarrow~x^3-0.125=0\\ &\begin{array}{c} \Leftrightarrow~(x-0.5)\underbrace{(x^2+0.5x+0.25)}_{}=0\\ \qquad\qquad正 \end{array} \end{align}

  4. $0.125$の$3$乗根， つまり$x^3 = 0.125$となる$x$は$0.5$である．よって

    \begin{align} \sqrt[3]{0.125}=\boldsymbol{0.5} \end{align}

$a$の$n$乗根の表し方でもみたように， 負の数$a$の$n$乗根は存在しないことがある． 以下では簡単のため，特にことわりのない限り正の数$a$の$n$乗根について考えることにする．

一般に，累乗根について，次のことが成り立つ．

累乗根の基本性質

$a > 0，b > 0$で，$m，n，l$が自然数のとき，次の等式が成り立つ．

  1. $\left(\sqrt[n]{a}~\right)^n=a$
  2. $\sqrt[n]{a}\sqrt[n]{b}=\sqrt[n]{ab} $
  3. $\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\dfrac{a}{b}}$
  4. $\left(\sqrt[n]{a}~\right)^m=\sqrt[n]{a^m}$
  5. $\sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}$
  6. $\sqrt[n]{a^m}=\sqrt[nl]{a^{ml}}$

この基本法則により，たとえば$\sqrt[4]{2}\sqrt[4]{8}$は2.と4.と1.を使い

\begin{align} &\sqrt[4]{2}\sqrt[4]{8}=\sqrt[4]{2\times8}=\sqrt[4]{2^4}=(\sqrt[4]{2})^4=2 \end{align}

と計算できる．

【証明】

  1. $\sqrt[n]{a}$の定義は，$n$乗して$a$になる数であるから，$\sqrt[n]{a}$を$n$乗すれば当然$a$になる．

  2. $\sqrt[n]{a}>0，\sqrt[n]{b}>0$より，$\sqrt[n]{a}\sqrt[n]{b}>0$であり，

    $\left(\sqrt[n]{a}\sqrt[n]{b}\right)^n=\left(\sqrt[n]{a}\right)^n\left(\sqrt[n]{b}\right)^n$ $\blacktriangleleft$指数法則の3.

    $=ab$ $\blacktriangleleft$指数法則の1.

    であるから，左辺の$\sqrt[n]{a}\sqrt[n]{b}$は，$ab$の$n$乗根のうち正のもの，すなわち$\sqrt[n]{ab}$を表す．

  3. $\sqrt[n]{a}>0，\sqrt[n]{b}>0$より，$\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}>0$であり

    $\left(\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}\right)^n=\dfrac{\left(\sqrt[n]{a}\right)^n}{\left(\sqrt[n]{b}\right)^n}$ $\blacktriangleleft$指数法則の3.

    $=\dfrac{a}{b}$ $\blacktriangleleft$指数法則の1.

    であるから，左辺の$\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}$は，$\dfrac{a}{b}$の$n$乗根のうち正のもの， すなわち$\sqrt[n]{\dfrac{a}{b}}$を表す．

暗記累乗根の基本性質の証明

指数法則を利用して，累乗の基本性質の4.～6.を証明せよ．

  • 4.$\left(\sqrt[n]{a}\right)^m>0$であり

    $\left\{\left(\sqrt[n]{a}\right)^m\right\}^n=\left(\sqrt[n]{a}\right)^{mn}$ $\blacktriangleleft$ 指数法則2.

    $=\left\{\left(\sqrt[n]{a}\right)^n\right\}^m$ $\blacktriangleleft$ 指数法則2.

    $=a^m$ $\blacktriangleleft$ 累乗根の基本性質1.

    であるから，左辺の$\left(\sqrt[n]{a}\right)^m$は，$a^m$の$n$乗根のうち正のものを表す． これは，右辺の$\sqrt[n]{a^m}$にほかならない．

  • 5.$\sqrt[m]{\sqrt[n]{a}}>0$であり

    $\left\{\sqrt[m]{\sqrt[n]{a}}\right\}^{mn}=\left\{\left(\sqrt[m]{\sqrt[n]{a}}\right)^m\right\}^n$ $\blacktriangleleft$ 指数法則2.

    $=\left(\sqrt[n]{a}\right)^n$ $\blacktriangleleft$ 累乗根の基本性質1.

    $=a$ $\blacktriangleleft$ 累乗根の基本性質1.

    であるから，左辺の$\sqrt[m]{\sqrt[n]{a}}$は，$a$の$mn$乗根のうち正のものを表す． これは，右辺の$\sqrt[mn]{a}$にほかならない．

  • 6.$\sqrt[n]{a^m}>0$であり

    $\left\{\sqrt[n]{a^m}\right\}^{nl}=\left\{\left(\sqrt[n]{a^m}\right)^n\right\}^l$ $\blacktriangleleft$ 指数法則2.

    $=\left({a^m}\right)^l$ $\blacktriangleleft$ 累乗根の基本性質1.

    $=a^{ml}$ $\blacktriangleleft$ 指数法則2.

    であるから，左辺の$\sqrt[n]{a^m}$は，$a^{ml}$の$nl$乗根のうち正のものを表す． これは，右辺の$\sqrt[nl]{a^{ml}}$にほかならない．

累乗根の値を求める-その2-

次の式を簡単にせよ．

  1. $\sqrt[3]{4}\sqrt[3]{16}$
  2. $\dfrac{\sqrt[5]{96}}{\sqrt[5]{3}}$
  3. $\sqrt[3]{216}$
  4. $\sqrt[3]{\sqrt{729}}$
  5. $\sqrt[6]{8}$
  6. $\sqrt[15]{27}$

  1. \begin{align} \sqrt[3]{4}\sqrt[3]{16}=\sqrt[3]{4\times16}\\ =\sqrt[3]{4^3}=\boldsymbol{4} \end{align} $\blacktriangleleft$ 累乗根の基本性質2.

  2. \begin{align} \dfrac{\sqrt[5]{96}}{\sqrt[5]{3}}=\sqrt[5]{\dfrac{96}{3}}\\ =\sqrt[5]{32}=\sqrt[5]{2^5}=\boldsymbol{2} \end{align} $\blacktriangleleft$ 累乗根の基本性質3.

  3. \[\sqrt[3]{216}=\sqrt[3]{6^3}=\boldsymbol{6}\]

  4. \begin{align} \sqrt[3]{\sqrt{729}}=\sqrt[6]{729}\\ =\sqrt[6]{3^6}=\boldsymbol{3} \end{align} $\blacktriangleleft$ 累乗根の基本性質5.

  5. \begin{align} \sqrt[6]{8}=\sqrt[6]{2^3}\\ =\boldsymbol{\sqrt{2}} \end{align} $\blacktriangleleft$ 累乗根の基本性質6.

  6. \begin{align} \sqrt[15]{27}=\sqrt[15]{3^3}\\ =\boldsymbol{\sqrt[5]{3}} \end{align} $\blacktriangleleft$ 累乗根の基本性質6.