空間ベクトルの内積
空間ベクトルの正射影
ベクトルのなす角の定義(空間)
ベクトルのなす角の定義

まず平面ベクトルの場合と同じように、空間ベクトルでもベクトルのなす角を定義する。
ベクトルのなす角の定義

$\vec{0}$ でない2つの空間ベクトル、$\vec{a}$、$\vec{b}$ に対して、点 $\text{O}$ を始点として \[\vec{a}=\overrightarrow{\text{OA}} , \vec{b}=\overrightarrow{\text{OB}}\] となるように点 $\text{A}$、$\text{B}$ をとる。このとき、$\angle\text{AOB}$ の大きさ $\theta$ は、$\vec{a}$、$\vec{b}$ によって決まる。この $\theta$ を、$\vec{a}$ と $\vec{b}$ のなす角とする。
なす角の取り得る範囲

なす角の取り得る範囲は、平面ベクトルの場合と同様に $0^\circ\leqq\theta\leqq180^\circ$ となる。
ベクトルの正射影と有向距離(空間)

平面ベクトルの場合と同じように,空間ベクトルでもベクトルの正射影と有向距離を定義する.
$\vec{0}$ でない2 つの空間ベクトル,$\vec{a},\vec{b}$ に対して,点$\text{O}$ を始点として
\[\vec{a} =\overrightarrow{\text{OA}} , \vec{b} =\overrightarrow{\text{OB}}\]となるように点$\text{A},\text{B}$ をとる.
いま,右図の点$\text{B}$ からから直線$\text{OA}$ に下ろした垂線の足を$\text{H}$ とする.このとき,$\overrightarrow{\text{OH}}$を$\vec{b}$ の$\vec{a}$ への正射影ベクトルといい$_{\vec{b}\rightarrow}\vec{a}$ と表す.正射影ベクトル$_{\vec{b}\rightarrow}\vec{a}$ は,$\vec{a},\vec{b}$ とそのなす角$\theta$ を用いて次のように表すことができる.
$\boldsymbol{0^\circ \leqq \theta \leqq 90^\circ}$ のとき
\begin{align} _{\vec{b}\rightarrow}\vec{a} &= \dfrac{\text{OH}}{\text{OA}}\overrightarrow{\text{OA}}\\ &= \dfrac{\text{OB}\cos \theta}{\text{OA}}\overrightarrow{\text{OA}}\\ &=\dfrac{\left|\vec{b}\right| \cos \theta}{\left|\vec{a}\right|}\vec{a} \end{align}
$\boldsymbol{90^\circ < \theta \leqq 180^\circ}$ のとき
\begin{align} _{\vec{b}\rightarrow}\vec{a} &= − \dfrac{\text{OH}}{\text{OA}}\overrightarrow{\text{OA}}\\ &= − \dfrac{\text{OB}\cos(180^\circ − \theta)}{\text{OA}}\overrightarrow{\text{OA}}\\ &=\dfrac{\left|\vec{b}\right| \cos \theta}{\left|\vec{a}\right|}\vec{a} \end{align}
つまり,$0^\circ \leqq \theta \leqq 180^\circ$ で$_{\vec{b}\rightarrow}\vec{a} =\dfrac{\left|\vec{b}\right| \cos \theta}{\left|\vec{a}\right|}\vec{a}$と表せる.この$\left|\vec{b}\right| \cos \theta$ の値のことを,$_{\vec{b}\rightarrow}\vec{a}$の有向距離または符号付長さという.
なお,$_{\vec{b}\rightarrow}\vec{a}$ の大きさは
\begin{align} \left|_{\vec{b}\rightarrow}\vec{a}\right| &= \left|\dfrac{\left|\vec{b}\right| \cos \theta}{\left|\vec{a}\right|}\vec{a}\right|\\ &=\dfrac{\left|\vec{b} \cos \theta \right|}{\left|\vec{a}\right|}\left|\vec{a}\right|\\ &=\left|\vec{b} \cos \theta \right| \end{align}で表される.
ベクトルの内積(空間)
ベクトルの内積の定義(空間)
平面ベクトルの場合と同じように,空間ベクトルでもベクトルの内積を定義 する.
任意の2 つの空間ベクトル,$\vec{a},\vec{b}$ に対して内積という演算$\vec{a} \cdot \vec{b}$ を次のように定義する.
$\boldsymbol{\vec{a} \neq \vec{0}}$ かつ$\boldsymbol{\vec{b} \neq \vec{0}}$ のとき
「$\vec{a}$ の大きさに,$_{\vec{b}\rightarrow}\vec{a}$ の有向距離をかけたもの」,すなわち
\[\vec{a} \cdot \vec{b} = \left|\vec{a}\right| \times \left|\vec{b}\right| \cos \theta\]とする.ここで,$\theta$ は$\vec{a}$ と$\vec{b}$ のなす角である.
$\boldsymbol{\vec{a} = \vec{0}}$ または$\boldsymbol{\vec{b} = \vec{0}}$ のとき
\[\vec{a} \cdot \vec{b} = 0\]とする.

空間の正射影ベクトルの内積での表し方
平面ベクトルの場合と同じように,空間ベクトルでも同様な形で,正射影ベク トルを内積で表すことができる.
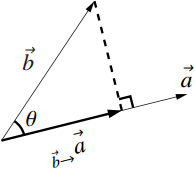
$\vec{b}$ の$\vec{a}$ への正射影ベクトル$_{\vec{b}\rightarrow}\vec{a}$ は
\begin{align} _{\vec{b}\rightarrow}\vec{a} &= \dfrac{\left|\vec{b}\right| \cos \theta}{\left|\vec{a}\right|}\vec{a}\\ &=\dfrac{\left|\vec{a}\right|\left|\vec{b}\right| \cos \theta}{\left|\vec{a}\right|^2}\vec{a}\\ &\because 分母分子に\left|\vec{a}\right| をかけた\\ &=\dfrac{\vec{a} \cdot \vec{b}}{\left|\vec{a}\right|^2}\vec{a}\\ &\because \vec{a} \cdot \vec{b} = \left|\vec{a}\right|\left|\vec{b}\right| \cos \theta \end{align}と表すことができる.
内積の計算法則(空間)
平面ベクトルの場合と同じように,空間ベクトルの内積でも,次のような計算 法則が成り立つ.
内積に関する計算法則
- 交換法則 \[\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}\]
- 結合法則 \[\vec{a} \cdot (k\vec{b}) = k(\vec{a} \cdot \vec{b})\]
- 分配法則 \[\vec{a} \cdot (\vec{b} +\vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c}\]
- \[\vec{a} \cdot \vec{a} = 0\]
【証明】は平面の時の内積に関する計算法則と同様.
成分表示された空間ベクトルの内積
成分表示された2 つの空間ベクトル,$\vec{a} = \left( \begin{array}{c} a_x\\ a_y\\ a_z\\ \end{array} \right), \vec{b} = \left( \begin{array}{c} b_x\\ b_y\\ b_z\\ \end{array} \right)$ の内積について考えてみよう.
まず,$\vec{e_x} = \left( \begin{array}{c} 1\\ 0\\ 0\\ \end{array} \right), \vec{e_y} = \left( \begin{array}{c} 0\\ 1\\ 0\\ \end{array} \right), \vec{e_z} = \left( \begin{array}{c} 0\\ 0\\ 1\\ \end{array} \right)$ について,それぞれのベクトルの大きさは$1$であり,どの2 つのベクトルのなす角も$90^\circ$ であるから
\begin{align} &\left|\vec{e_x}\right|=\left|\vec{e_y}\right|=\left|\vec{e_z}\right|= 1 \tag{1}\label{seibunhyouzisaretakuukanbekutorunonaiseki1}\\ &\vec{e_x} \cdot \vec{e_y} = 0 , \vec{e_y} \cdot \vec{e_z} = 0 , \vec{e_z} \cdot \vec{e_x} = 0 \tag{2}\label{seibunhyouzisaretakuukanbekutorunonaiseki2} \end{align}が成り立つ.
ここで,$\vec{a}$ は
\begin{align} \vec{a} = \left( \begin{array}{c} a_x\\ a_y\\ a_z\\ \end{array} \right) &= \left( \begin{array}{c} a_x\\ 0\\ 0\\ \end{array} \right) + \left( \begin{array}{c} 0\\ a_y\\ 0\\ \end{array} \right) + \left( \begin{array}{c} 0\\ 0\\ a_z\\ \end{array} \right)\\ &= a_x \left( \begin{array}{c} 1\\ 0\\ 0\\ \end{array} \right) + a_y \left( \begin{array}{c} 0\\ 1\\ 0\\ \end{array} \right) + a_z \left( \begin{array}{c} 0\\ 0\\ 1\\ \end{array} \right) \end{align}であるから,$\vec{a}$ を$\vec{e_x},\vec{e_y},\vec{e_z}$ に分解すると
\[\vec{a} = a_x \vec{e_x} + a_y \vec{e_y} + a_z \vec{e_z} \tag{3}\label{seibunhyouzisaretakuukanbekutorunonaiseki3}\]となる.
同様にして
\[\vec{b} = b_x \vec{e_x} + b_y \vec{e_y} + b_z \vec{e_z} \tag{4}\label{seibunhyouzisaretakuukanbekutorunonaiseki4}\]となる.
よって, $\eqref{seibunhyouzisaretakuukanbekutorunonaiseki3},\eqref{seibunhyouzisaretakuukanbekutorunonaiseki4}$より
\begin{align} \vec{a} \cdot \vec{b} &= (a_x \vec{e_x} + a_y \vec{e_y} + a_z \vec{e_z}) \\ &\quad \cdot (b_x \vec{e_x} + b_y \vec{e_y} + b_z \vec{e_z})\\ &= a_xb_x \left|\vec{e_x}\right|^2 + a_yb_y \left|\vec{e_y}\right|^2 + a_zb_z \left|\vec{e_z}\right|^2 \quad \because \eqref{seibunhyouzisaretakuukanbekutorunonaiseki2}\\ &= a_xb_x + a_yb_y + a_zb_z \qquad \because \eqref{seibunhyouzisaretakuukanbekutorunonaiseki1} \end{align} となる.空間ベクトルの内積
次の2 つのベクトルの内積の値とそのなす角$\theta (0^\circ \leqq \theta \leqq 180^\circ)$ を求めよ.
- $(−1, − 2, 1),(1, − 1, 2)$
- $(1, 0, − 1),(1, 2, − 2) $
- \[\vec{a} \cdot \vec{b} = −1 \cdot 1 − 2 \cdot (−1) + 1 \cdot 2 = \boldsymbol{3}\]
$\cos \theta =\dfrac{\vec{a} \cdot \vec{b}}{\left|\vec{a}\right|\left|\vec{b}\right|}$ であるので,
\begin{align} &\cos \theta \\ &= \dfrac{3}{ \sqrt{(−1)^2 + (−2)^2 + 1^2} \sqrt{1^2 + (−1)^2 + 2^2} }\\ &=\dfrac{3}{ \sqrt{6}\sqrt{6} }=\dfrac{1}{2} \end{align}$0^\circ \leqq \theta \leqq 180^\circ$ より,$\boldsymbol{\theta = 60^\circ}$
- \[\vec{a} \cdot \vec{b} = 1 \cdot 1 + 0 \cdot 2 − 1 \cdot (−2) =\boldsymbol{3}\]
$\cos \theta =\dfrac{\vec{a} \cdot \vec{b}}{\left|\vec{a}\right|\left|\vec{b}\right|}$ であるので,
\begin{align} &\cos \theta \\ &= \dfrac{3}{ \sqrt{1^2 + 0^2 + (-1)^2} \sqrt{1^2 + 2^2 + (-2)^2} }\\ &=\dfrac{3}{ \sqrt{2}\sqrt{9} }=\dfrac{1}{\sqrt{2}} \end{align}$0^\circ \leqq \theta \leqq 180^\circ$ より,$\boldsymbol{\theta = 45^\circ}$
空間ベクトルの垂直条件
平面ベクトルの場合と同じように,空間ベクトルでもベクトルの垂直を定義する.
$\vec{0}$ でない2 つのベクトル,$\vec{a}$ と$\vec{b}$ のなす角が$90^\circ$ とき,$\vec{a}$ と$\vec{b}$ は垂直であるといい,$\boldsymbol{\vec{a}\perp\vec{b}}$と表す.また,$\vec{0}$ はすべてのベクトルに対し垂直と定める.
このとき,$\vec{a}$ と$\vec{b}$ の内積は,$\vec{a} \cdot \vec{b} = 0$ となる.逆に,$\vec{a} \cdot \vec{b} = 0$ ならば$\vec{a}\perp\vec{b}$ といえる.つまり
\[\vec{a}\perp\vec{b} \Longleftrightarrow\vec{a} \cdot \vec{b} = 0\]である.
また,成分表示された2 つのベクトル,$\vec{a} = \left( \begin{array}{c} a_x\\ a_y\\ a_z\\ \end{array} \right)$ と$\vec{b} = \left( \begin{array}{c} b_x\\ b_y\\ b_z\\ \end{array} \right)$ が垂直であるとき
\[ \left( \begin{array}{c} a_x\\ a_y\\ a_z\\ \end{array} \right) \cdot \left( \begin{array}{c} b_x\\ b_y\\ b_z\\ \end{array} \right) = 0 \Longleftrightarrow a_xb_x + a_yb_y + a_zb_z = 0\] が成り立つ.空間ベクトルの垂直条件
無題

正四面体$\text{O-ABC}$ で,$\text{OA}\perp\text{OB}$ が垂直であることを証明せよ.
正四面体であるので
\[\overrightarrow{\text{OA}} \cdot \overrightarrow{\text{OB}} =\overrightarrow{\text{OB}} \cdot\overrightarrow{\text{OC}}=\overrightarrow{\text{OC}} \cdot\overrightarrow{\text{OA}}\]より
\begin{align} \overrightarrow{\text{OA}} \cdot \overrightarrow{\text{BC}} &=\overrightarrow{\text{OA}} \cdot (\overrightarrow{\text{OC}} −\overrightarrow{\text{OB}})\\ &=\overrightarrow{\text{OA}} \cdot \overrightarrow{\text{OC}} −\overrightarrow{\text{OA}} \cdot \overrightarrow{\text{OB}} = 0 \end{align}以上から,$\text{OA}\perp\text{OB}$ であることが示せた.
空間ベクトルの内積と垂直条件
無題

1 辺の長さ2 の正四面体$\text{ABCD}$ がある.$\text{AB}$の中点を$\text{M},\text{CD}$ の中点を$\text{N}$ とする.$\overrightarrow{\text{DA}} = \vec{a},\overrightarrow{\text{DB}} = \vec{b},\overrightarrow{\text{DC}} = \vec{c}$とおくとき,以下の問いに答えよ.
- $\vec{a} \cdot \vec{b}$ の値を求めよ.
- $\overrightarrow{\text{MN}}$ を$\vec{a},\vec{b},\vec{c}$ で表せ.
- $\text{MN}\perp\text{AB}$ であることを証明せよ.
- $\left|\vec{a} + \vec{b} +\vec{c}\right|$を求めよ.
- $\overrightarrow{\text{DM}}$ と$\overrightarrow{\text{DC}}$ のなす角の余弦を求めよ.
- \[\vec{a} \cdot \vec{b} = 2 \cdot 2 \cdot \cos 60^\circ= \boldsymbol{2}\]
- \begin{align} \overrightarrow{\text{MN}} &=\overrightarrow{\text{DN}} −\overrightarrow{\text{DM}}\\ &= \dfrac{1}{2}\vec{c} − \dfrac{1}{2} (\vec{a} + \vec{b}) \\ &=\boldsymbol{\dfrac{1}{2} (−\vec{a} − \vec{b} + \vec{c})} \end{align}
$\overrightarrow{\text{AB}} = \vec{b} − \vec{a}$ であるので
\begin{align} \overrightarrow{\text{MN}} \cdot \overrightarrow{\text{AB}} &=\dfrac{1}{2}(−\vec{a} − \vec{b} +\vec{c}) \cdot (\vec{b} − \vec{a})\\ &= \dfrac{1}{2}\left(−\vec{a} \cdot \vec{b} + \left|\vec{a}\right|^2 − \left|\vec{b}\right|^2 \right.\\ &\qquad \left.+ \vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{c} − \vec{a} \cdot \vec{c}\right) \end{align}ここで,1. と$\text{ABCD}$ が正四面体であることから,$\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{c} = \vec{c} \cdot \vec{a} = 2$であるので
\[\overrightarrow{\text{MN}} \cdot \overrightarrow{\text{AB}} = \dfrac{1}{2} (−2 + 4 − 4 + 2 + 2 − 2) = 0\]したがって,$\text{MN}\perp\text{AB}$ である.
-
\begin{align}
\left|\vec{a} + \vec{b} +\vec{c}\right|^2
&= \left|\vec{a}\right|^2
+ \left|\vec{b}\right|^2
+ \left|\vec{c}\right|^2\\
&\qquad+ 2\left(
\vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{a} +\vec{c} \cdot \vec{a}
\right)\\
&= 4 + 4 + 4 + 2(2 + 2 + 2) = 24
\end{align}
したがって,$ \boldsymbol{\left|\vec{a} + \vec{b} +\vec{c}\right| = 2\sqrt{6}}$ である.
$\triangle \text{DAB}$ は正三角形であり,$\text{M}$ が$\text{AB}$ の中点であることから
\[\left|\overrightarrow{\text{DM}}\right| =\left|\overrightarrow{\text{AD}}\right| \sin 60^\circ=\sqrt{3}\]となり,また
\begin{align} \overrightarrow{\text{DM}} \cdot \overrightarrow{\text{DC}} &= \dfrac{1}{2} (\vec{a} + \vec{b}) \cdot \vec{c}\\ &=\dfrac{1}{2}\left(\vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c}\right)= 2 \end{align}である.したがって,$\overrightarrow{\text{DM}}\cdot \overrightarrow{\text{DC}}$ のなす角を$\theta$とすると
\[\cos \theta =\dfrac{\overrightarrow{\text{DM}} \cdot \overrightarrow{\text{DC}}}{ \left|\overrightarrow{\text{DM}}\right|\cdot \left|\overrightarrow{\text{DC}}\right|} = \dfrac{2}{2 \cdot \sqrt{3}}=\boldsymbol{\dfrac{1}{\sqrt{3}}}\]