三角比の拡張
これまでは、直角三角形を用いて鋭角の三角比を考えてきた。より一般的な三角形を分析するための準備として、ここでは三角比の考えを直角・鈍角・$0^\circ$へと拡張し、$0^\circ$から$180^\circ$までの三角比を統一的に扱おう。
座標と三角比の関係
単位円
単位円
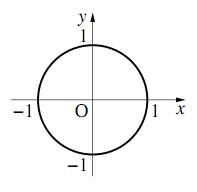
座標平面上の原点 $\text{O}$ を中心とする半径 $1$ の円を単位円 (unit circle) という。
三角比は、この単位円を用いて($90^\circ$ 以上に)拡張される。
三角比の拡張について
三角比の定義を、斜辺が $1$ である直角三角形 $\text{OPQ}$ において考えてみよう。
斜辺の長さが $1$ である直角三角形
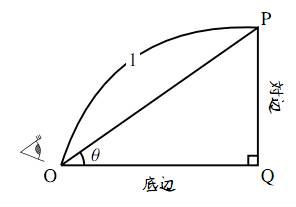
すると、正弦、余弦、正接はそれぞれ
\begin{align}
\sin{\theta}=&\dfrac{\text{PQ}}{\text{OP}}=\text{PQ}\\
\cos{\theta}=&\dfrac{\text{OQ}}{\text{PO}}=\text{OQ}\\
\tan{\theta}=&\dfrac{\text{QP}}{\text{OQ}}=\dfrac{\sin{\theta}}{\cos{\theta}}
\end{align}
と書ける。つまり、斜辺の長さが $1$ である直角三角形では
「対辺の長さは $\sin\theta$ の値を表し、底辺の長さは $\cos\theta$ の値を表す」
ことがわかる。
直角三角形を単位円の中に描く
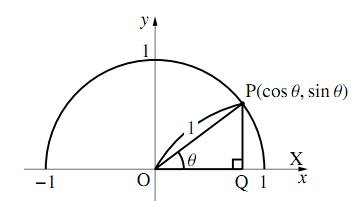
この $\triangle{\text{OPQ}}$ を、図のように単位円の(上半分の)中に描いてみよう。そのようにすれば、
- $\text{P}$ の $x$ 座標が $\cos\theta$
- $\text{P}$ の $y$ 座標が $\sin\theta$
このように、「単位円周上の点の座標」として三角比をとらえなおすと、角度が鋭角でなくても三角比を考えることができる。そこで、$0^\circ\leqq\theta\leqq180^\circ$ の範囲にある角 $\theta$ の三角比を、次のように定義しなおそう。
三角比の拡張
三角比の拡張
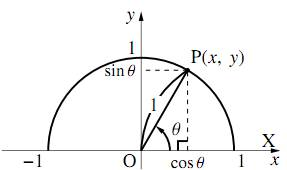
点 $\text{O}$ を原点とする座標平面上に単位円の上半分をとり、その周上に一点 $\text{P}$ をとる。
$x$ 軸の正の部分 $\text{OX}$ に対し、$\angle\text{POX}$ を $\theta(0^\circ\leqq\theta\leqq180^\circ)$ とするとき \begin{align} &\cos\theta=(点\text{P}のx座標)\\ &\sin\theta=(点\text{P}のy座標)\\ &\tan\theta=\dfrac{(点\text{P}のy座標)}{(点\text{P}のx座標)}=(直線\text{OP}の傾き) \end{align} とする。
ただし、点 $\text{P}$ の $x$ 座標が $0$ のとき、つまり $\theta=90^\circ$ のときは $\tan\theta$ を定義しない。
たとえば、$\theta$ が鈍角のときは次のようになる。
- 例:$120^\circ$ の三角比図より、 \begin{align} \cos120^\circ&=-\dfrac{1}{2}\\ \sin120^\circ&=\dfrac{\sqrt{3}}{2}\\ \tan120^\circ&=-\sqrt{3} \end{align} ($\triangle{\text{OPQ}}$ が $\text{QO}:\text{OP}:\text{PQ}=1:2:\sqrt{3}$ の直角三角形であることに注意しよう。)

- 例:$180^\circ$ の三角比図より、 \begin{align} \cos180^\circ&=-1\\ \sin180^\circ&=0\\ \tan180^\circ&=0 \end{align}

三角比の値のまとめ
角度が $0^\circ$、$30^\circ$、$45^\circ$、$60^\circ$、$90^\circ$、$120^\circ$、$135^\circ$、$150^\circ$、$180^\circ$ の場合の三角比は、頭の中で次のような図を思い描き、素早く求められるようになろう。
$0^\circ\leqq\theta\leqq180^\circ$ までの三角比
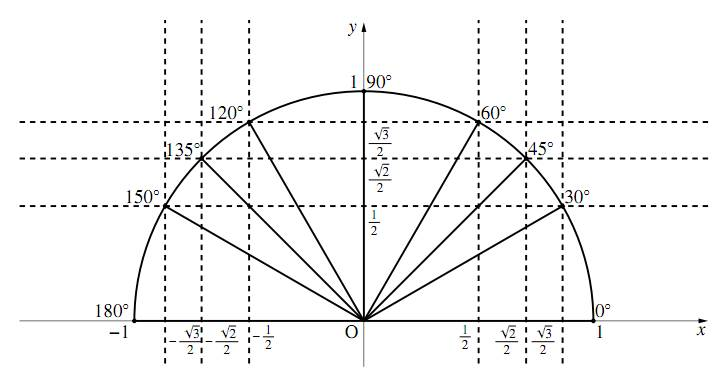
有名角の三角比
上の図をもとに下の表を完成させよ。
| $\theta$ | $0^\circ$ | $30^\circ$ | $45^\circ$ | $60^\circ$ | $90^\circ$ | $120^\circ$ | $135^\circ$ | $150^\circ$ | $180^\circ$ | |
| $\sin\theta$ | ||||||||||
| $\cos\theta$ | ||||||||||
| $\tan\theta$ |
| $\theta$ | $0^\circ$ | $30^\circ$ | $45^\circ$ | $60^\circ$ | $90^\circ$ | |
| $\sin\theta$ | $0$ | $\dfrac{1}{2}$ | $\dfrac{\sqrt{2}}{2}$ | $\dfrac{\sqrt{3}}{2}$ | $1$ | |
| $\cos\theta$ | $1$ | $\dfrac{\sqrt{3}}{2}$ | $\dfrac{\sqrt{2}}{2}$ | $\dfrac{1}{2}$ | $0$ | |
| $\tan\theta$ | $0$ | $\dfrac{1}{\sqrt{3}}$ | $1$ | $\sqrt{3}$ | なし |
| $\theta$ | $120^\circ$ | $135^\circ$ | $150^\circ$ | $180^\circ$ | |
| $\sin\theta$ | $\dfrac{\sqrt{3}}{2}$ | $\dfrac{\sqrt{2}}{2}$ | $\dfrac{1}{2}$ | $0$ | |
| $\cos\theta$ | $-\dfrac{1}{2}$ | $-\dfrac{\sqrt{2}}{2}$ | $-\dfrac{\sqrt{3}}{2}$ | $-1$ | |
| $\tan\theta$ | $-\sqrt{3}$ | $-1$ | $-\dfrac{1}{\sqrt{3}}$ | $0$ |
三角比を含む方程式と不等式
三角比を含む方程式
以下の式を満たす $\theta$ を求めよ。ただし $0^\circ\leqq\theta\leqq180^\circ$ とする。
- $\cos\theta =-\dfrac{\sqrt{3}}{2}$
- $\sin\theta=\dfrac{\sqrt{2}}{2}$
- $\tan\theta=-\sqrt{3}$
- $\sin\theta=1$

図のように、上半分の単位円周上において、$x$ 座標が $-\dfrac{\sqrt{3}}{2}$ である点を取る。
このとき、$\triangle{\text{OPQ}}$ は辺の長さが $1:2:\sqrt{3}$ の直角三角形なので \[\angle{\text{POQ}}=30^\circ\] つまり、$\theta=180^\circ-30^\circ=\boldsymbol{150^\circ}$。

図のように、上半分の単位円周上において、$y$ 座標が $\dfrac{\sqrt{2}}{2}$ である点を取る。
そのような点は2つ存在し、$\triangle{\text{OPQ}}$、$\triangle\text{OP'Q'}$ とも 直角二等辺三角形であるので \[\angle{\text{POQ}}=45^\circ~,~\angle\text{P'OQ'}=45^\circ\] つまり、$\boldsymbol{\theta=45^\circ}$、または、$\theta=180^\circ-45^\circ=\boldsymbol{135^\circ}$。

動径の傾きが $\tan$ に一致するので、図のように、傾き $-\sqrt{3}$ の直線を引く。
$\triangle{\text{OPQ}}$ は辺の長さが $1:2:\sqrt{3}$ の直角三角形なので \[\angle{\text{OPQ}}=60^\circ\] つまり、$\theta=180^\circ-60^\circ=\boldsymbol{120^\circ}$。

上半分の単位円周上において、$y$ 座標が $1$ である点を取ればよい。
このとき、図より、$\boldsymbol{\theta=90^\circ}$。
吹き出し三角比を含む方程式と不等式
有名角の三角比に限れば、三角比から角度を求めるときと、角度から三角比を求めるときに重要なことは、次のことに限られる。
つまり、条件に合うよう単位円と動径を描き、うまく垂線を引いて
- 3辺の長さが $1,~\dfrac{\sqrt{2}}{2},~\dfrac{\sqrt{2}}{2}$ の直角三角形を作ることができる。
- 3辺の長さが $1,~\dfrac{\sqrt{3}}{2},~\dfrac{1}{2}$ の直角三角形を作ることができる。
- 直角三角形を作る必要はない。
三角比を含む不等式
以下の式を満たす $\theta$ を求めよ。ただし $0^\circ\leqq\theta\leqq180^\circ$ とする。
- $\cos\theta\leqq-\dfrac{\sqrt{3}}{2}$
- $\sin\theta\gt\dfrac{\sqrt{2}}{2}$
- $\tan\theta\gt-\sqrt{3}$
- 上半分の単位円周上において \[(x座標の値)\leqq-\dfrac{\sqrt{3}}{2}\] であればよい。そのようになるのは、図の太線部分であるので $\boldsymbol{150^\circ\leqq\theta\leqq180^\circ}$。

- 上半分の単位円周上において \[(y座標の値)\gt\dfrac{\sqrt{2}}{2}\] であればよい。そのようになるのは、図の太線部分であるので $\boldsymbol{45^\circ\lt\theta\lt135^\circ}$。

- 上半分の単位円周上において \[(動径の傾き)\gt-\sqrt{3}\] であればよい。そのようになるのは、図の太線部分であるので $\boldsymbol{0^\circ\leqq\theta\lt90^\circ,120^\circ\lt\theta\leqq180^\circ}$。

拡張された三角比の相互関係
拡張された三角比の相互関係について
拡張された三角比においても、三角比の相互関係で学んだ三角比の相互関係 \begin{align} &\tan\theta=\dfrac{\sin\theta}{\cos\theta},~\sin^2\theta+\cos^2\theta=1\\ &1+\dfrac{1}{\tan^2\theta}=\dfrac{1}{\sin^2\theta},~\tan^2\theta+1=\dfrac{1}{\cos^2\theta} \end{align} が成り立つ。以下でこれらのことを確認してみよう。
拡張された三角比の相互関係
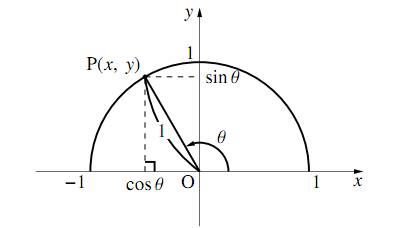
図の単位円において \[\cos\theta=x~,~\sin\theta=y\] であるから、$\tan\theta$ は \[\tan{\theta}=\dfrac{y}{x}=\dfrac{\sin\theta}{\cos\theta}\] と表すことができる。つまり \[\tan\theta=\dfrac{\sin\theta}{\cos\theta}\tag{1}\label{kakutyosaretasankakuhinosougokankenituite1}\] が成り立つ。また、三平方の定理より、$x^2+y^2=1$ であるから \[\sin^2\theta+\cos^2\theta=1\tag{2}\label{kakutyosaretasankakuhinosougokankenituite2}\] が成り立ち、$\eqref{kakutyosaretasankakuhinosougokankenituite2}$ の両辺を $\sin^2\theta$ で割って、$\tan\theta=\dfrac{\sin\theta}{\cos\theta}$ を用いると \begin{align} &1+\dfrac{\cos^2\theta}{\sin^2\theta}=\dfrac{1}{\sin^2\theta}\\ \therefore~~&1+\dfrac{1}{\tan^2\theta}=\dfrac{1}{\sin^2\theta}\tag{3}\label{kakutyosaretasankakuhinosougokankenituite3} \end{align} また、$\eqref{kakutyosaretasankakuhinosougokankenituite2}$ の両辺を $\cos^2\theta$ で割って、$\tan\theta=\dfrac{\sin\theta}{\cos\theta}$ を用いると \begin{align} &\dfrac{\sin^2\theta}{\cos^2\theta}+1=\dfrac{1}{\cos^2\theta}\\ \therefore~~&\tan^2\theta+1=\dfrac{1}{\cos^2\theta}\tag{4}\label{kakutyosaretasankakuhinosougokankenituite4} \end{align}
拡張された三角比の相互関係
角 $\theta$ が $0^\circ\leqq\theta\leqq180^\circ$ のとき、次の式が成り立つ。
- $\sin\theta$、$\cos\theta$、$\tan\theta$ の関係 \[\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}\]
- $\sin\theta$ と $\cos\theta$ の関係 \[\sin^2{\theta}+\cos^2{\theta}=1\]
- $\tan\theta$ と $\sin\theta$ の関係 \[1+\dfrac{1}{\tan^2{\theta}}=\dfrac{1}{\sin^2{\theta}}\]
- $\cos\theta$ と $\tan\theta$ の関係 \[\tan^2{\theta}+1=\dfrac{1}{\cos^2{\theta}}\]
三角比どうしの関係と同じ問を、拡張された三角比の相互関係を使って解いてみよう。ただし、今回は $0^\circ$ から $180^\circ$ までの範囲で考える。
拡張された三角比の相互関係の利用
拡張された三角比の相互関係を使って次の問に答えよ。ただし $0^\circ\leqq\alpha\leqq 180^\circ$ である。
- $\sin\alpha=\dfrac{3}{5}$ のとき、$\cos\alpha$、$\tan\alpha$ の値を求めよ。
- $\cos\alpha=\dfrac{1}{3}$ のとき、$\sin\alpha$、$\tan\alpha$ の値を求めよ。
- $\tan\alpha=7$ のとき、$\cos\alpha$、$\sin\alpha$ の値を求めよ。
- $\blacktriangleleft$ 拡張された三角比の相互関係より$\sin^2\alpha+\cos^2\alpha=1$ \begin{align} \cos^2\alpha=1-\sin^2\alpha=1-\left(\dfrac{3}{5}\right)^2=\dfrac{16}{25} \end{align} よって、$\cos\alpha=\pm\sqrt{\dfrac{16}{25}}=\boldsymbol{\pm\dfrac{4}{5}}$。$\blacktriangleleft$ 拡張された三角比の相互関係よりまた、$\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}$ より、$\blacktriangleleft$ $\cos\alpha=\pm\dfrac{4}{5},~\tan\alpha=\pm\dfrac{3}{4}$(複合同順)と書いてもよい\begin{align} &\cos\alpha=\dfrac{4}{5}のとき\tan\alpha=\dfrac{\dfrac{3}{5}}{\dfrac{4}{5}}=\boldsymbol{\dfrac{3}{4}}\\ &\cos\alpha=-\dfrac{4}{5}のとき\\ &\tan\alpha=\dfrac{\dfrac{3}{5}}{-\dfrac{4}{5}}=\boldsymbol{-\dfrac{3}{4}} \end{align}
- $\blacktriangleleft$ 拡張された三角比の相互関係より$\sin^2\alpha+\cos^2\alpha=1$ より \begin{align} \sin^2\alpha=1-\cos^2\alpha=1-\left(\dfrac{1}{3}\right)^2=\dfrac{8}{9} \end{align}$\blacktriangleleft$ $0^\circ\leqq\alpha\leqq180^\circ$ のとき、定義から $\sin\alpha\geqq0$。$\sin\alpha\geqq0$ なので、$\sin\alpha=\sqrt{\dfrac{8}{9}}=\boldsymbol{\dfrac{2\sqrt{2}}{3}}$。$\blacktriangleleft$ 拡張された三角比の相互関係よりまた、$\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}$ より \begin{align} \tan\alpha=\dfrac{\dfrac{2\sqrt{2}}{3}}{\dfrac{1}{3}}=\boldsymbol{2\sqrt{2}} \end{align}
- $\blacktriangleleft$ 拡張された三角比の相互関係より$\tan^2\alpha+1=\dfrac{1}{\cos^2\alpha}$ より \begin{align} \cos^2\alpha=\dfrac{1}{1+\tan^2\alpha}=\dfrac{1}{1+7^2}=\dfrac{1}{50} \end{align} よって、$\cos\alpha=\pm\sqrt{\dfrac{1}{50}}=\pm\dfrac{\sqrt{2}}{10}$ である。$\blacktriangleleft$ 拡張された三角比の相互関係よりまた、$\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}$ より \begin{align} &7=\dfrac{\sin\alpha}{\pm\dfrac{\sqrt{2}}{10}}\\ \therefore~~&\sin\alpha=7\times\left(\pm\dfrac{\sqrt{2}}{10}\right)=\pm\dfrac{7\sqrt{2}}{10} \end{align}$\blacktriangleleft$ $\tan\alpha$ の値が正であるから、$\cos\alpha$ の値も正である$0\leqq\sin\alpha$ であるので、$\sin\alpha=-\dfrac{7\sqrt{2}}{10}$ は不適。
よって \[\boldsymbol{\cos\alpha=\dfrac{\sqrt{2}}{10}~,~\sin\alpha=\dfrac{7\sqrt{2}}{10}}\]
三角比の計算
次の式を簡単にせよ。
- $(\sin\theta+\cos\theta)^2+(\sin\theta-\cos\theta)^2$
- $\dfrac{\cos\theta}{1+\sin\theta}-\dfrac{\cos\theta}{1-\sin\theta}$
- $\blacktriangleleft$ 拡張された三角比の相互関係より\begin{align} &(\sin \theta+\cos\theta)^2+(\sin\theta-\cos\theta)^2\\ =&\sin^2\theta+2\sin\theta\cos\theta+\cos^2\theta\\ &\qquad+\sin^2\theta -2\sin\theta\cos\theta+\cos^2\theta\\ =&2(\sin^2\theta+\cos^2\theta)\\ =&\boldsymbol{2} \end{align}
- $\blacktriangleleft$ 拡張された三角比の相互関係より\begin{align} &\dfrac{\cos\theta}{1+\sin\theta}-\dfrac{\cos\theta}{1-\sin\theta}\\ =&\dfrac{\cos\theta\left(1-\sin\theta\right)-\cos\theta\left(1+\sin\theta\right)} {\left(1+\sin\theta\right)\left(1-\sin\theta\right)}\\ =&\dfrac{-2\cos\theta\sin\theta}{1-\sin^2\theta}\\ =&-\dfrac{2\cos\theta\sin\theta}{\cos^2\theta}\\ =&-\dfrac{2\sin\theta}{\cos\theta}\\ =&\boldsymbol{-2\tan\theta} \end{align}
$90^\circ+\theta$ の三角比
図のように、単位円周上に角$\theta$ の動径 $\text{OP}$ と角 $90^\circ+\theta(=\theta'とする)$ の動径 $\text{OP'}$ をとる。
$90^\circ+\theta$ の三角比
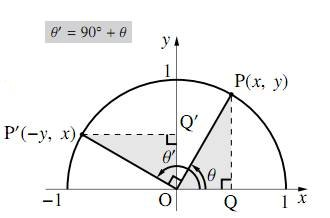
点 $\text{P}$ の座標を $(x,y)$ とすると、$\triangle\text{OPQ}$ と $\triangle\text{OP'Q'}$ は合同なので、点 $\text{P'}$ の座標は $(-y,x)$ となるから \[\sin\theta'=x=\cos\theta\] \[\cos\theta'=y=-\sin\theta\] \[\tan\theta'=\dfrac{x}{-y}=-\dfrac{x}{y}=-\dfrac{1}{\tan\theta}\] と表すことができる。
ここで、$\theta'=90^\circ+\theta$ であるから、次のようにまとめることができる。
$90^\circ+\theta$ の三角比
$90^\circ+\theta$ の三角比
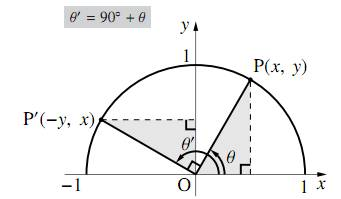
角 $\theta$ が $0^\circ\leqq\theta\leqq90^\circ$ の三角比において \[\sin(90^\circ+\theta)=\cos\theta\] \[\cos(90^\circ+\theta)=-\sin\theta\] \[\tan(90^\circ+\theta)=-\dfrac{1}{\tan\theta}\] が成り立つ。
吹き出し$90^\circ+\theta$ の三角比
「$90^\circ+\theta$ の三角比は $\theta$ だけを使った三角比で表せる」ということを覚えておくのが大切であり、この式は暗記するようなものではない。必要なときに、上の図を描いて素早く導出できるようにしておけばよい。
これより、$90^\circ\lt\theta\leqq180^\circ$ の三角比は、$0^\circ\lt\theta\leqq90^\circ$ の三角比になおして、その値を求めることができる。
$90^\circ+\theta$ の三角比の利用
次の式を満たすように $\fbox{A}$ の中に $90^\circ$ より小さい角を入れよ。
- $\sin100^\circ=\cos\fbox{A}$
- $\cos179^\circ=-\sin\fbox{A}$
- $\tan125^\circ=-\dfrac{1}{\tan\fbox{A}}$
- $\blacktriangleleft$ $\sin(90^\circ+\theta)=\cos\theta$$\sin100^\circ=\sin(90^\circ+10^\circ)=\cos10^\circ$
- $\blacktriangleleft$ $\cos(90^\circ+\theta)=-\sin\theta$$\cos179^\circ=\cos(90^\circ+89^\circ)=-\sin89^\circ$
- $\blacktriangleleft$ $\tan(90^\circ+\theta)=-\dfrac{1}{\tan\theta}$$\tan125^\circ=\tan(90^\circ+35^\circ)=-\dfrac{1}{\tan35^\circ}$
$180^\circ-\theta$ の三角比
図のように、単位円周上に角 $\theta$ の動径 $\text{OP}$ と角 $180^\circ-\theta(=θ'とする)$ の動径 $\text{OP'}$ をとる。
$180^\circ-\theta$ の三角比
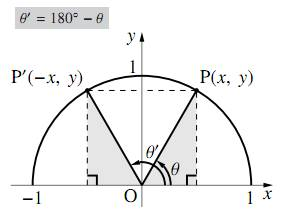
点 $\text{P}$ の座標を $(x,y)$ とすると、点 $\text{P'}$ の座標は $(-y,x)$ となるから \[\sin\theta'=y=\sin\theta\] \[\cos\theta'=-x=-\cos\theta\] \[\tan\theta'=\dfrac{y}{-x}=-\dfrac{y}{x}=-\tan\theta\] と表すことができる。
ここで、$\theta'=180^\circ-\theta$ であるから、次のようにまとめることができる。
$180^\circ-\theta$ の三角比
角$\theta$ が $0^\circ\leqq\theta\leqq180^\circ$ の三角比において \[\sin(180^\circ-\theta)=\sin\theta\] \[\cos(180^\circ-\theta)=-\cos\theta\] \[\tan(180^\circ-\theta)=-\tan\theta\] が成り立つ。
吹き出し$180^\circ-\theta$ の三角比
「$180^\circ-\theta$ の三角比は $\theta$ だけを使った三角比で表せる」ということを覚えておくのが大切であり、この式も暗記するようなものではない。やはり、必要なときに、上の図を描いて素早く導出できるようにしておけばよい。
これからも、$90^\circ\lt\theta\leqq180^\circ$ の三角比は、$0^\circ\lt\theta\leqq90^\circ$ の三角比になおして、その値を求めることができる。
$180^\circ-\theta$ の三角比の利用
次の式を満たすように $\fbox{A}$ の中に $90^\circ$ より小さい角を入れよ。
- $\sin100^\circ=\sin\fbox{A}$
- $\cos179^\circ=-\cos\fbox{A}$
- $\tan125^\circ=-\tan\fbox{A}$
- $\blacktriangleleft$ $\sin(180^\circ-\theta)=\sin\theta$$\sin100^\circ=\sin(180^\circ-80^\circ)=\sin80^\circ$
- $\blacktriangleleft$ $\cos(180^\circ-\theta)=-\cos\theta$$\cos179^\circ=\cos(180^\circ-1^\circ)=-\cos1^\circ$
- $\blacktriangleleft$ $\tan(180^\circ-\theta)=-\tan\theta$$\tan125^\circ=\tan(180^\circ-55^\circ)=-\tan55^\circ$