三角比の応用
ここでは、三角形の分析を行うための基本ツールである、正弦定理や余弦定理などを学んでいこう。
三角形の面積と三角比
三角形の面積
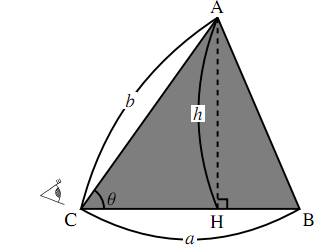
$\triangle\text{ABC}$ の面積を、2辺の長さ $a$、$b$ と、その間の角度 $\theta$ を用いて表すことを考えてみよう。次の左の図は $\theta$ が鋭角の場合、次の右の図は $\theta$ が鈍角の場合を表している。
鋭角三角形
鈍角三角形
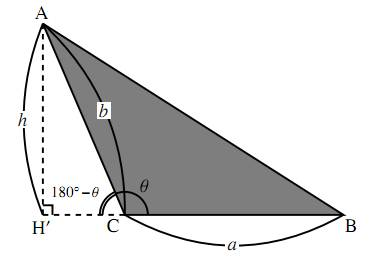
前の図の三角形において、底辺を $a$ とすれば高さは $h$ であるから、三角形の面積 $S$ はどちらも $S=\dfrac{ah}{2}$ である。
ここで高さ $h$ は、前の左の図では、$h=b\sin\theta$ であり、前の右の図でも \[h=b\sin(180^\circ-\theta)=b\sin\theta\] である。すなわち、鋭角三角形、鈍角三角形のどちらの場合でも、高さは $h=b\sin\theta$ となり \[S=\dfrac{ah}{2}=\dfrac{a{\cdot}b\sin\theta}{2}=\dfrac{1}{2}ab\sin\theta\] と表すことができる(これは、$\theta=90^\circ$ の直角三角形の場合も含んでいる)。
三角形の面積
三角形の面積
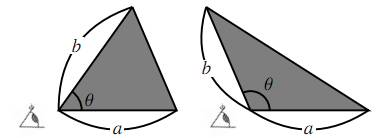
図の三角形の面積 $S$ は \[S=\dfrac{1}{2}ab\sin\theta\] で表せる。
吹き出し三角形の面積
$a$ を底辺とみれば $b\sin\theta$ が高さを表し、$b$ を底辺とみれば $a\sin\theta$ が高さを表す。
正弦定理
正弦定理について
三角形の3つの頂点を通る円を、その三角形の外接円 (circumscribed circle) という。1つの三角形に対し、外接円は1つに定まる。
いま、図のような三角形とその外接円を考える。
三角形と外接円

このとき、外接円の半径を $R$ とすると \[\dfrac{a}{\sin{A}}=2R\] が成り立つ。これを、正弦定理 (sine theorem) という。この式が成り立つことを、鋭角三角形、直角三角形、鈍角三角形の場合に分けて以下にみていこう。
$\angle{A}$ が鋭角のとき
図のように、$\triangle\text{ABC}$ に外接する円に、直径 $\text{BD}$ を引くと、下図のようになる。


いま、図の $\triangle\text{DBC}$ は直角三角形となるから $\sin{D}=\dfrac{a}{2R}$ であり、円周角の定理より $A=D$ であるから \[\sin{A}=\dfrac{a}{2R}\qquad\therefore\dfrac{a}{\sin{A}}=2R\] となり成立。
$\angle{A}$ が直角のとき
$\sin{A}=1,a=2R$ であるから
\[\dfrac{a}{\sin{A}}=\dfrac{a}{1}=2R\] となり成立。
暗記正弦定理の導出
上の続きとして、$\angle{A}$ が鈍角のとき正弦定理が成り立つことを証明せよ。
鈍角三角形での正弦定理

$\triangle\text{ABC}$ に外接する円に、直径 $\text{BD}$ を引くと、図のようになる。
いま、図の $\triangle\text{DBC}$ は直角三角形となるから $\sin{D}=\dfrac{a}{2R}$ であり、円に内接する四角形の性質から $A=180^\circ-D$ であるから \begin{align} &\sin{(180^\circ-A)}=\sin{A}=\dfrac{a}{2R}\\ \therefore&~\dfrac{a}{\sin{A}}=2R \end{align} となり成立。
正弦定理
正弦定理

$\triangle\text{ABC}$ において \[\dfrac{a}{\sin{A}}=\dfrac{b}{\sin{B}}=\dfrac{c}{\sin{C}}=2R\] が成り立つ。
ただし、$R$ は $\triangle\text{ABC}$ の外接円の半径とする。吹き出し正弦定理について
正弦定理の使い方は主に2つある。1つは、$\dfrac{a}{\sin{A}}=\dfrac{b}{\sin{B}}$ の関係から、辺の長さや角度を求めることである。この場合、正弦定理は2辺と2角について成り立つ関係式であることに注意しよう。2つの角と1つの辺がわかれば、この関係式からもう1つの辺の長さが計算できる。そしてもう1つの使い方は、外接円の半径 $R$ を求めることである。内接円ではないので注意しよう(内接円の半径については三角形の面積と内接円の半径を参照のこと)。
正弦定理の利用~その1~
$\triangle\text{ABC}$ において、$a=12$、$A=45^\circ$、$B=60^\circ$ のとき、$b$ の値を求めよ。また、$\triangle\text{ABC}$ の外接円の半径を求めよ。
正弦定理の利用

正弦定理より、$\dfrac{a}{\sin{A}}=\dfrac{b}{\sin{B}}$ であるから \begin{align} b=&\dfrac{a\sin{B}}{\sin{A}}\\ =&\dfrac{12\sin60^\circ}{\sin45^\circ}\\ =&\dfrac{12\times\dfrac{\sqrt{3}}{2}}{\dfrac{\sqrt{2}}{2}}\\ =&\boldsymbol{6\sqrt{6}} \end{align} 同じく正弦定理より、$2R=\dfrac{a}{\sin{A}}$ であるから \begin{align} R=&\dfrac{a}{2\sin{A}}\\ =&\dfrac{12}{2\sin45^\circ}\\ =&\dfrac{12}{2\times\dfrac{\sqrt{2}}{2}}\\ =&\dfrac{12}{\sqrt{2}}\\ =&\boldsymbol{6\sqrt{2}} \end{align}
吹き出し正弦定理について
図形の角度や長さを求める問題では、図示してから考えるようにしよう。図形的感覚を磨くのに役に立ち、単純なミスを防ぐ効果もある。
正弦定理の利用~その2~
$\triangle\text{ABC}$ において、各辺の長さが $a:b:c=2:4:5$ であるとき、$\sin{A}:\sin{B}:\sin{C}$ の値を求めよ。
正弦定理の利用

$\triangle\text{ABC}$ の外接円の半径を $R$ とすると、正弦定理より \[a=2R\sin{A},~b=2R\sin{B},~c=2R\sin{C}\] であるから \begin{align} &2R\sin{A}:2R\sin{B}:2R\sin{C}=2:4:5\\ \therefore~&\boldsymbol{\sin{A}:\sin{B}:\sin{C}=2:4:5} \end{align}
余弦定理
第1余弦定理
第1余弦定理

図のような三角形の2つの角と2辺の長さの間に次の関係式が成り立つ。
\[c=b\cos{A}+a\cos{B}\] これを、第1余弦定理 (first cosine theorem) という。
この式が成り立つことを、$A$ が鋭角、直角、鈍角の場合に分けて、以下に見ていこう。
$A$ が鋭角のとき

線分 $\text{AB}$ 上に、図のように垂線 $\text{CH}$ をひくと \begin{align} &b\cos{A}+a\cos{B}\\ =&\text{AH}+\text{BH}\\ =&\text{AB}=c \end{align} となり成立。
$A$ が直角のとき

$A=90^\circ$ より、$\cos{A}=0$ となるので \begin{align} &b\overbrace{\cos{A}}^{0}+a\cos{B}\\ =&a\cos{B}\\ =&c \end{align} となり成立。
暗記第1余弦定理の導出
上の続きとして、$A$ が鈍角のときも第1余弦定理が成り立つことを証明せよ。
第1余弦定理の導出

直線 $\text{AB}$ 上に、図のように垂線 $\text{CH}$ をひくと \begin{align} &b\cos{A}+a\cos{B}\\ =&-b\cos(180^\circ-A)+a\cos{B}\\ =&-\text{AH}+\text{BH}\\ =&\text{BH}-\text{AH}=\text{AB}=c \end{align}
第1余弦定理
第1余弦定理

$\triangle\text{ABC}$ において \begin{align} &c=b\cos{A}+a\cos{B}\\ &b=a\cos{C}+c\cos{A}\\ &a=c\cos{B}+b\cos{C} \end{align} が成り立つ。
吹き出し第1余弦定理
第1余弦定理のイメージ

この定理は、ある角から見たときに左右2つの辺を向かいの辺に押しつぶす感じで覚えると良い。
第2余弦定理(余弦定理)
第2余弦定理(余弦定理)

三角形の1つの角と3辺の長さの間に次の関係式が成り立つ。 \[a^2=b^2+c^2-2bc\cos\theta\] これを、第2余弦定理 (second cosine thorem) といい、単に余弦定理 (cosine thorem) というときにはこちらを指す。
この式が成り立つことを、$A$ が鋭角、直角、鈍角の場合に分けて、以下に見ていこう。
$A$ が鋭角のとき

図のように、線分 $\text{AB}$ 上に垂線 $\text{CH}$ をひき、$\triangle\text{BCH}$ に三平方の定理を用いると \begin{align} &a^2=\text{BC}^2=\text{CH}^2+\text{BH}^2\\ =&\left(b\sin{A}\right)^2+\left(c-b\cos{A}\right)^2\\ =&b^2\sin^2{A}+c^2-2bc\cos{A}+b^2\cos^2{A}\\ =&b^2(\sin^2{A}+\cos^2{A})+c^2-2bc\cos{A}\\ =&b^2+c^2-2bc\cos{A} \end{align} となり成立。
$A$ が直角のとき

$A=90^\circ$ より、$\cos{A}=0$ となるので \begin{align} &a^2=\text{BC}^2=\text{CA}^2+\text{AB}^2\\ =&b^2+c^2\\ =&b^2+c^2-2bc\underbrace{\cos{A}}_{0} \end{align} となり成立。
暗記余弦定理の導出
上の続きとして、$A$ が鈍角のときも余弦定理が成り立つことを証明せよ。
余弦定理の導出

直線 $\text{AB}$ 上に、図のように垂線 $\text{CH}$ をひき、$\triangle\text{BCH}$ に三平方の定理を用いると \begin{align} &a^2=\text{BC}^2=\text{CH}^2+\text{BH}^2\\ =&\left\{b\sin\left(180^\circ-A\right)\right\}^2+\\ &\qquad\left\{c+b\cos\left(180^\circ-A\right)\right\}^2\\ =&\left(b\sin{A}\right)^2+\left(c-b\cos{A}\right)^2\\ &\blacktriangleleft 180^\circ-\thetaの三角比\\ =&b^2\sin^2{A}+c^2-2bc\cos{A}+b^2\cos^2{A}\\ =&b^2(\sin^2{A}+\cos^2{A})+c^2-2bc\cos{A}\\ &\blacktriangleleft 拡張された三角比の相互関係\\ =&b^2+c^2-2bc\cos{A} \end{align} となり成立。
第2余弦定理(余弦定理)
第2余弦定理(余弦定理)

$\triangle\text{ABC}$ において \begin{align} &a^2=b^2+c^2-2bc\cos{A}\\ &b^2=c^2+a^2-2ca\cos{B}\\ &c^2=a^2+b^2-2ab\cos{C} \end{align} が成り立つ。
吹き出し第2余弦定理(余弦定理)
余弦定理の主な使い方は、$a^2=b^2+c^2-2bc\cos{A}$ などの関係式から、辺の長さや角度を求めることである。余弦定理は3辺と1角について成り立つ関係式であることに注意しよう。たとえば、2つの辺と1つの角がわかれば、この 関係式からもう1つの辺の長さが計算できるという具合である。
余弦定理の利用~その1~
$\triangle\text{ABC}$ において、$b=3$、$c=4\sqrt{2}$、$A=45^\circ$ のとき、$a$ の値を求めよ。
余弦定理の利用

点 $\text{A}$ からみる余弦定理より \begin{align} a^2=&b^2+c^2-2ab\cos{A}\\ =&3^2+\left(4\sqrt{2}\right)^2-2\cdot3\cdot4\sqrt{2}\cos{45^\circ}\\ =&9+32-24\sqrt{2}\times\dfrac{\sqrt{2}}{2}=17 \end{align} よって、$\boldsymbol{a=\sqrt{17}}$ である。
$\triangle\text{ABC}$ の3辺の長さ $a,b,c$ がわかっているとき、$\angle\text{A}$ の大きさは、余弦定理を変形した \[\cos{A}=\dfrac{b^2+c^2-a^2}{2bc}\] から求めることができる。
余弦定理の利用~その2~
$\triangle\text{ABC}$ において、$a=\sqrt{21}$、$b=4$、$c=5$ のとき、$A$ の値を求めよ。また、$\cos{B}$ を求めよ。
余弦定理の利用

$\triangle\text{ABC}$ に点 $\text{A}$ からみる余弦定理を用いると、$\cos{A}=\dfrac{b^2+c^2-a^2}{2bc}$。これより \[\cos{A}=\dfrac{4^2+5^2-\left(\sqrt{21}\ \right)^2}{2\cdot4\cdot5}=\dfrac{1}{2}\] よって、$\boldsymbol{A=60^\circ}$ となる。
同じく余弦定理を用いると、$\cos{B}=\dfrac{c^2+a^2-b^2}{2ca}$。これより \begin{align} \cos{B}&=\frac{5^2+\left(\sqrt{21}\ \right)^2-4^2}{2\cdot5\cdot\sqrt{21}}\\ &=\dfrac{30}{10\sqrt{21}}=\boldsymbol{\dfrac{\sqrt{21}}{7}} \end{align}