ベクトルの内積（空間）

ベクトルの内積の定義（空間）

平面ベクトルの場合と同じように，空間ベクトルでもベクトルの内積を定義する．

任意の2 つの空間ベクトル， $\vec{a}，\vec{b}$ に対して内積という演算 $\vec{a} \cdot \vec{b}$ を次のように定義する．

$\boldsymbol{\vec{a} \neq \vec{0}}$ かつ $\boldsymbol{\vec{b} \neq \vec{0}}$ のとき
「 $\vec{a}$ の大きさに， $_{\vec{b}\rightarrow}\vec{a}$ の有向距離をかけたもの」，すなわち
$\vec{a} \cdot \vec{b} = \left|\vec{a}\right| \times \left|\vec{b}\right| \cos \theta$
とする．ここで， $\theta$ は $\vec{a}$ と $\vec{b}$ のなす角である．
$\boldsymbol{\vec{a} = \vec{0}}$ または $\boldsymbol{\vec{b} = \vec{0}}$ のとき
$\vec{a} \cdot \vec{b} = 0$
とする．

空間の正射影ベクトルの内積での表し方

平面ベクトルの場合と同じように，空間ベクトルでも同様な形で，正射影ベクトルを内積で表すことができる．

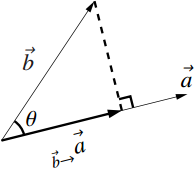
$\vec{b}$ の $\vec{a}$ への正射影ベクトル $_{\vec{b}\rightarrow}\vec{a}$ は

$\begin{align} _{\vec{b}\rightarrow}\vec{a} &= \dfrac{\left|\vec{b}\right| \cos \theta}{\left|\vec{a}\right|}\vec{a}\\ &=\dfrac{\left|\vec{a}\right|\left|\vec{b}\right| \cos \theta}{\left|\vec{a}\right|^2}\vec{a}\\ &\because 分母分子に\left|\vec{a}\right| をかけた\\ &=\dfrac{\vec{a} \cdot \vec{b}}{\left|\vec{a}\right|^2}\vec{a}\\ &\because \vec{a} \cdot \vec{b} = \left|\vec{a}\right|\left|\vec{b}\right| \cos \theta \end{align}$

と表すことができる．

内積の計算法則（空間）

平面ベクトルの場合と同じように，空間ベクトルの内積でも，次のような計算法則が成り立つ．

内積に関する計算法則

交換法則 $\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}$
結合法則 $\vec{a} \cdot (k\vec{b}) = k(\vec{a} \cdot \vec{b})$
分配法則 $\vec{a} \cdot (\vec{b} +\vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c}$
$\vec{a} \cdot \vec{a} = 0$

【証明】は平面の時の内積に関する計算法則と同様．

成分表示された空間ベクトルの内積

成分表示された2 つの空間ベクトル， $\vec{a} = \left( \begin{array}{c} a_x\\ a_y\\ a_z\\ \end{array} \right), \vec{b} = \left( \begin{array}{c} b_x\\ b_y\\ b_z\\ \end{array} \right)$ の内積について考えてみよう．

まず， $\vec{e_x} = \left( \begin{array}{c} 1\\ 0\\ 0\\ \end{array} \right), \vec{e_y} = \left( \begin{array}{c} 0\\ 1\\ 0\\ \end{array} \right), \vec{e_z} = \left( \begin{array}{c} 0\\ 0\\ 1\\ \end{array} \right)$ について，それぞれのベクトルの大きさは $1$ であり，どの2 つのベクトルのなす角も $90^\circ$ であるから

$\begin{align} &\left|\vec{e_x}\right|=\left|\vec{e_y}\right|=\left|\vec{e_z}\right|= 1 \tag{1}\label{seibunhyouzisaretakuukanbekutorunonaiseki1}\\ &\vec{e_x} \cdot \vec{e_y} = 0 , \vec{e_y} \cdot \vec{e_z} = 0 , \vec{e_z} \cdot \vec{e_x} = 0 \tag{2}\label{seibunhyouzisaretakuukanbekutorunonaiseki2} \end{align}$

が成り立つ．

ここで， $\vec{a}$ は

$\begin{align} \vec{a} = \left( \begin{array}{c} a_x\\ a_y\\ a_z\\ \end{array} \right) &= \left( \begin{array}{c} a_x\\ 0\\ 0\\ \end{array} \right) + \left( \begin{array}{c} 0\\ a_y\\ 0\\ \end{array} \right) + \left( \begin{array}{c} 0\\ 0\\ a_z\\ \end{array} \right)\\ &= a_x \left( \begin{array}{c} 1\\ 0\\ 0\\ \end{array} \right) + a_y \left( \begin{array}{c} 0\\ 1\\ 0\\ \end{array} \right) + a_z \left( \begin{array}{c} 0\\ 0\\ 1\\ \end{array} \right) \end{align}$

であるから， $\vec{a}$ を $\vec{e_x}，\vec{e_y}，\vec{e_z}$ に分解すると

$\vec{a} = a_x \vec{e_x} + a_y \vec{e_y} + a_z \vec{e_z} \tag{3}\label{seibunhyouzisaretakuukanbekutorunonaiseki3}$

となる．

同様にして

$\vec{b} = b_x \vec{e_x} + b_y \vec{e_y} + b_z \vec{e_z} \tag{4}\label{seibunhyouzisaretakuukanbekutorunonaiseki4}$

となる．

よって， $\eqref{seibunhyouzisaretakuukanbekutorunonaiseki3}，\eqref{seibunhyouzisaretakuukanbekutorunonaiseki4}$ より

$\begin{align} \vec{a} \cdot \vec{b} &= (a_x \vec{e_x} + a_y \vec{e_y} + a_z \vec{e_z}) \\ &\quad \cdot (b_x \vec{e_x} + b_y \vec{e_y} + b_z \vec{e_z})\\ &= a_xb_x \left|\vec{e_x}\right|^2 + a_yb_y \left|\vec{e_y}\right|^2 + a_zb_z \left|\vec{e_z}\right|^2 \quad \because \eqref{seibunhyouzisaretakuukanbekutorunonaiseki2}\\ &= a_xb_x + a_yb_y + a_zb_z \qquad \because \eqref{seibunhyouzisaretakuukanbekutorunonaiseki1} \end{align}$ となる．

空間ベクトルの内積

次の2 つのベクトルの内積の値とそのなす角 $\theta (0^\circ \leqq \theta \leqq 180^\circ)$ を求めよ．

$(−1, − 2, 1)，(1, − 1, 2)$
$(1, 0, − 1)，(1, 2, − 2)$

空間ベクトルの内積の解答

$\vec{a} \cdot \vec{b} = −1 \cdot 1 − 2 \cdot (−1) + 1 \cdot 2 = \boldsymbol{3}$
$\cos \theta =\dfrac{\vec{a} \cdot \vec{b}}{\left|\vec{a}\right|\left|\vec{b}\right|}$ であるので，
$\begin{align} &\cos \theta \\ &= \dfrac{3}{ \sqrt{(−1)^2 + (−2)^2 + 1^2} \sqrt{1^2 + (−1)^2 + 2^2} }\\ &=\dfrac{3}{ \sqrt{6}\sqrt{6} }=\dfrac{1}{2} \end{align}$
$0^\circ \leqq \theta \leqq 180^\circ$ より， $\boldsymbol{\theta = 60^\circ}$
$\vec{a} \cdot \vec{b} = 1 \cdot 1 + 0 \cdot 2 − 1 \cdot (−2) =\boldsymbol{3}$
$\cos \theta =\dfrac{\vec{a} \cdot \vec{b}}{\left|\vec{a}\right|\left|\vec{b}\right|}$ であるので，
$\begin{align} &\cos \theta \\ &= \dfrac{3}{ \sqrt{1^2 + 0^2 + (-1)^2} \sqrt{1^2 + 2^2 + (-2)^2} }\\ &=\dfrac{3}{ \sqrt{2}\sqrt{9} }=\dfrac{1}{\sqrt{2}} \end{align}$
$0^\circ \leqq \theta \leqq 180^\circ$ より， $\boldsymbol{\theta = 45^\circ}$

空間ベクトルの垂直条件

平面ベクトルの場合と同じように，空間ベクトルでもベクトルの垂直を定義する．

$\vec{0}$ でない2 つのベクトル， $\vec{a}$ と $\vec{b}$ のなす角が $90^\circ$ とき， $\vec{a}$ と $\vec{b}$ は垂直であるといい， $\boldsymbol{\vec{a}\perp\vec{b}}$ と表す．また， $\vec{0}$ はすべてのベクトルに対し垂直と定める．

このとき， $\vec{a}$ と $\vec{b}$ の内積は， $\vec{a} \cdot \vec{b} = 0$ となる．逆に， $\vec{a} \cdot \vec{b} = 0$ ならば $\vec{a}\perp\vec{b}$ といえる．つまり

$\vec{a}\perp\vec{b} \Longleftrightarrow\vec{a} \cdot \vec{b} = 0$

である．

また，成分表示された2 つのベクトル， $\vec{a} = \left( \begin{array}{c} a_x\\ a_y\\ a_z\\ \end{array} \right)$ と $\vec{b} = \left( \begin{array}{c} b_x\\ b_y\\ b_z\\ \end{array} \right)$ が垂直であるとき

$\left( \begin{array}{c} a_x\\ a_y\\ a_z\\ \end{array} \right) \cdot \left( \begin{array}{c} b_x\\ b_y\\ b_z\\ \end{array} \right) = 0 \Longleftrightarrow a_xb_x + a_yb_y + a_zb_z = 0$ が成り立つ．

空間ベクトルの垂直条件

無題

正四面体 $\text{O-ABC}$ で， $\text{OA}\perp\text{OB}$ が垂直であることを証明せよ．

空間ベクトルの垂直条件の解答

正四面体であるので

$\overrightarrow{\text{OA}} \cdot \overrightarrow{\text{OB}} =\overrightarrow{\text{OB}} \cdot\overrightarrow{\text{OC}}=\overrightarrow{\text{OC}} \cdot\overrightarrow{\text{OA}}$

より

$\begin{align} \overrightarrow{\text{OA}} \cdot \overrightarrow{\text{BC}} &=\overrightarrow{\text{OA}} \cdot (\overrightarrow{\text{OC}} −\overrightarrow{\text{OB}})\\ &=\overrightarrow{\text{OA}} \cdot \overrightarrow{\text{OC}} −\overrightarrow{\text{OA}} \cdot \overrightarrow{\text{OB}} = 0 \end{align}$

以上から， $\text{OA}\perp\text{OB}$ であることが示せた．

空間ベクトルの内積と垂直条件

無題

1 辺の長さ2 の正四面体 $\text{ABCD}$ がある． $\text{AB}$ の中点を $\text{M}，\text{CD}$ の中点を $\text{N}$ とする． $\overrightarrow{\text{DA}} = \vec{a}，\overrightarrow{\text{DB}} = \vec{b}，\overrightarrow{\text{DC}} = \vec{c}$ とおくとき，以下の問いに答えよ．

$\vec{a} \cdot \vec{b}$ の値を求めよ．
$\overrightarrow{\text{MN}}$ を $\vec{a}，\vec{b}，\vec{c}$ で表せ．
$\text{MN}\perp\text{AB}$ であることを証明せよ．
$\left|\vec{a} + \vec{b} +\vec{c}\right|$ を求めよ．
$\overrightarrow{\text{DM}}$ と $\overrightarrow{\text{DC}}$ のなす角の余弦を求めよ．

空間ベクトルの内積と垂直条件の解答

$\vec{a} \cdot \vec{b} = 2 \cdot 2 \cdot \cos 60^\circ= \boldsymbol{2}$
$\begin{align} \overrightarrow{\text{MN}} &=\overrightarrow{\text{DN}} −\overrightarrow{\text{DM}}\\ &= \dfrac{1}{2}\vec{c} − \dfrac{1}{2} (\vec{a} + \vec{b}) \\ &=\boldsymbol{\dfrac{1}{2} (−\vec{a} − \vec{b} + \vec{c})} \end{align}$
$\overrightarrow{\text{AB}} = \vec{b} − \vec{a}$ であるので
$\begin{align} \overrightarrow{\text{MN}} \cdot \overrightarrow{\text{AB}} &=\dfrac{1}{2}(−\vec{a} − \vec{b} +\vec{c}) \cdot (\vec{b} − \vec{a})\\ &= \dfrac{1}{2}\left(−\vec{a} \cdot \vec{b} + \left|\vec{a}\right|^2 − \left|\vec{b}\right|^2 \right.\\ &\qquad \left.+ \vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{c} − \vec{a} \cdot \vec{c}\right) \end{align}$
ここで，1. と $\text{ABCD}$ が正四面体であることから， $\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{c} = \vec{c} \cdot \vec{a} = 2$ であるので
$\overrightarrow{\text{MN}} \cdot \overrightarrow{\text{AB}} = \dfrac{1}{2} (−2 + 4 − 4 + 2 + 2 − 2) = 0$
したがって， $\text{MN}\perp\text{AB}$ である．
$\begin{align} \left|\vec{a} + \vec{b} +\vec{c}\right|^2 &= \left|\vec{a}\right|^2 + \left|\vec{b}\right|^2 + \left|\vec{c}\right|^2\\ &\qquad+ 2\left( \vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{a} +\vec{c} \cdot \vec{a} \right)\\ &= 4 + 4 + 4 + 2(2 + 2 + 2) = 24 \end{align}$
したがって， $\boldsymbol{\left|\vec{a} + \vec{b} +\vec{c}\right| = 2\sqrt{6}}$ である．
$\triangle \text{DAB}$ は正三角形であり， $\text{M}$ が $\text{AB}$ の中点であることから
$\left|\overrightarrow{\text{DM}}\right| =\left|\overrightarrow{\text{AD}}\right| \sin 60^\circ=\sqrt{3}$
となり，また
$\begin{align} \overrightarrow{\text{DM}} \cdot \overrightarrow{\text{DC}} &= \dfrac{1}{2} (\vec{a} + \vec{b}) \cdot \vec{c}\\ &=\dfrac{1}{2}\left(\vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c}\right)= 2 \end{align}$
である．したがって， $\overrightarrow{\text{DM}}\cdot \overrightarrow{\text{DC}}$ のなす角を $\theta$ とすると
$\cos \theta =\dfrac{\overrightarrow{\text{DM}} \cdot \overrightarrow{\text{DC}}}{ \left|\overrightarrow{\text{DM}}\right|\cdot \left|\overrightarrow{\text{DC}}\right|} = \dfrac{2}{2 \cdot \sqrt{3}}=\boldsymbol{\dfrac{1}{\sqrt{3}}}$