座標と三角比の関係
単位円
単位円
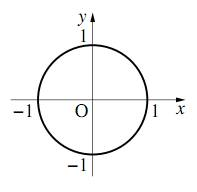
座標平面上の原点 $\text{O}$ を中心とする半径 $1$ の円を単位円 (unit circle) という。
三角比は、この単位円を用いて($90^\circ$ 以上に)拡張される。
三角比の拡張について
三角比の定義を、斜辺が $1$ である直角三角形 $\text{OPQ}$ において考えてみよう。
斜辺の長さが $1$ である直角三角形
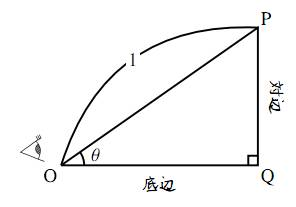
すると、正弦、余弦、正接はそれぞれ
\begin{align}
\sin{\theta}=&\dfrac{\text{PQ}}{\text{OP}}=\text{PQ}\\
\cos{\theta}=&\dfrac{\text{OQ}}{\text{PO}}=\text{OQ}\\
\tan{\theta}=&\dfrac{\text{QP}}{\text{OQ}}=\dfrac{\sin{\theta}}{\cos{\theta}}
\end{align}
と書ける。つまり、斜辺の長さが $1$ である直角三角形では
「対辺の長さは $\sin\theta$ の値を表し、底辺の長さは $\cos\theta$ の値を表す」
ことがわかる。
直角三角形を単位円の中に描く
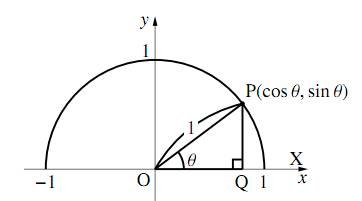
この $\triangle{\text{OPQ}}$ を、図のように単位円の(上半分の)中に描いてみよう。そのようにすれば、
- $\text{P}$ の $x$ 座標が $\cos\theta$
- $\text{P}$ の $y$ 座標が $\sin\theta$
このように、「単位円周上の点の座標」として三角比をとらえなおすと、角度が鋭角でなくても三角比を考えることができる。そこで、$0^\circ\leqq\theta\leqq180^\circ$ の範囲にある角 $\theta$ の三角比を、次のように定義しなおそう。
三角比の拡張
三角比の拡張
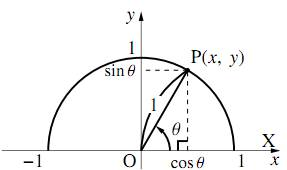
点 $\text{O}$ を原点とする座標平面上に単位円の上半分をとり、その周上に一点 $\text{P}$ をとる。
$x$ 軸の正の部分 $\text{OX}$ に対し、$\angle\text{POX}$ を $\theta(0^\circ\leqq\theta\leqq180^\circ)$ とするとき \begin{align} &\cos\theta=(点\text{P}のx座標)\\ &\sin\theta=(点\text{P}のy座標)\\ &\tan\theta=\dfrac{(点\text{P}のy座標)}{(点\text{P}のx座標)}=(直線\text{OP}の傾き) \end{align} とする。
ただし、点 $\text{P}$ の $x$ 座標が $0$ のとき、つまり $\theta=90^\circ$ のときは $\tan\theta$ を定義しない。
たとえば、$\theta$ が鈍角のときは次のようになる。
- 例:$120^\circ$ の三角比図より、 \begin{align} \cos120^\circ&=-\dfrac{1}{2}\\ \sin120^\circ&=\dfrac{\sqrt{3}}{2}\\ \tan120^\circ&=-\sqrt{3} \end{align} ($\triangle{\text{OPQ}}$ が $\text{QO}:\text{OP}:\text{PQ}=1:2:\sqrt{3}$ の直角三角形であることに注意しよう。)

- 例:$180^\circ$ の三角比図より、 \begin{align} \cos180^\circ&=-1\\ \sin180^\circ&=0\\ \tan180^\circ&=0 \end{align}

三角比の値のまとめ
角度が $0^\circ$、$30^\circ$、$45^\circ$、$60^\circ$、$90^\circ$、$120^\circ$、$135^\circ$、$150^\circ$、$180^\circ$ の場合の三角比は、頭の中で次のような図を思い描き、素早く求められるようになろう。
$0^\circ\leqq\theta\leqq180^\circ$ までの三角比
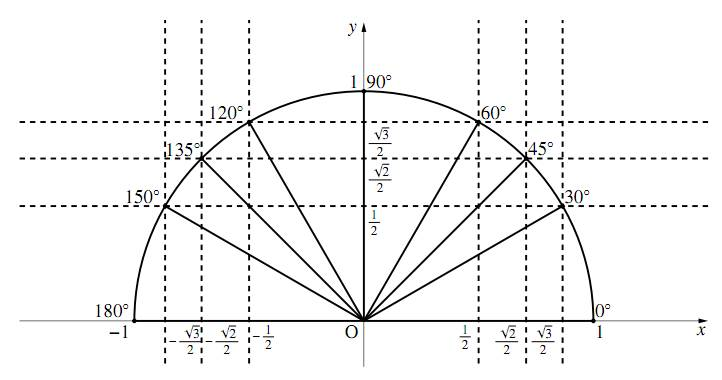
有名角の三角比
上の図をもとに下の表を完成させよ。
| $\theta$ | $0^\circ$ | $30^\circ$ | $45^\circ$ | $60^\circ$ | $90^\circ$ | $120^\circ$ | $135^\circ$ | $150^\circ$ | $180^\circ$ | |
| $\sin\theta$ | ||||||||||
| $\cos\theta$ | ||||||||||
| $\tan\theta$ |
| $\theta$ | $0^\circ$ | $30^\circ$ | $45^\circ$ | $60^\circ$ | $90^\circ$ | |
| $\sin\theta$ | $0$ | $\dfrac{1}{2}$ | $\dfrac{\sqrt{2}}{2}$ | $\dfrac{\sqrt{3}}{2}$ | $1$ | |
| $\cos\theta$ | $1$ | $\dfrac{\sqrt{3}}{2}$ | $\dfrac{\sqrt{2}}{2}$ | $\dfrac{1}{2}$ | $0$ | |
| $\tan\theta$ | $0$ | $\dfrac{1}{\sqrt{3}}$ | $1$ | $\sqrt{3}$ | なし |
| $\theta$ | $120^\circ$ | $135^\circ$ | $150^\circ$ | $180^\circ$ | |
| $\sin\theta$ | $\dfrac{\sqrt{3}}{2}$ | $\dfrac{\sqrt{2}}{2}$ | $\dfrac{1}{2}$ | $0$ | |
| $\cos\theta$ | $-\dfrac{1}{2}$ | $-\dfrac{\sqrt{2}}{2}$ | $-\dfrac{\sqrt{3}}{2}$ | $-1$ | |
| $\tan\theta$ | $-\sqrt{3}$ | $-1$ | $-\dfrac{1}{\sqrt{3}}$ | $0$ |
三角比を含む方程式と不等式
三角比を含む方程式
以下の式を満たす $\theta$ を求めよ。ただし $0^\circ\leqq\theta\leqq180^\circ$ とする。
- $\cos\theta =-\dfrac{\sqrt{3}}{2}$
- $\sin\theta=\dfrac{\sqrt{2}}{2}$
- $\tan\theta=-\sqrt{3}$
- $\sin\theta=1$

図のように、上半分の単位円周上において、$x$ 座標が $-\dfrac{\sqrt{3}}{2}$ である点を取る。
このとき、$\triangle{\text{OPQ}}$ は辺の長さが $1:2:\sqrt{3}$ の直角三角形なので \[\angle{\text{POQ}}=30^\circ\] つまり、$\theta=180^\circ-30^\circ=\boldsymbol{150^\circ}$。

図のように、上半分の単位円周上において、$y$ 座標が $\dfrac{\sqrt{2}}{2}$ である点を取る。
そのような点は2つ存在し、$\triangle{\text{OPQ}}$、$\triangle\text{OP'Q'}$ とも 直角二等辺三角形であるので \[\angle{\text{POQ}}=45^\circ~,~\angle\text{P'OQ'}=45^\circ\] つまり、$\boldsymbol{\theta=45^\circ}$、または、$\theta=180^\circ-45^\circ=\boldsymbol{135^\circ}$。

動径の傾きが $\tan$ に一致するので、図のように、傾き $-\sqrt{3}$ の直線を引く。
$\triangle{\text{OPQ}}$ は辺の長さが $1:2:\sqrt{3}$ の直角三角形なので \[\angle{\text{OPQ}}=60^\circ\] つまり、$\theta=180^\circ-60^\circ=\boldsymbol{120^\circ}$。

上半分の単位円周上において、$y$ 座標が $1$ である点を取ればよい。
このとき、図より、$\boldsymbol{\theta=90^\circ}$。
吹き出し三角比を含む方程式と不等式
有名角の三角比に限れば、三角比から角度を求めるときと、角度から三角比を求めるときに重要なことは、次のことに限られる。
つまり、条件に合うよう単位円と動径を描き、うまく垂線を引いて
- 3辺の長さが $1,~\dfrac{\sqrt{2}}{2},~\dfrac{\sqrt{2}}{2}$ の直角三角形を作ることができる。
- 3辺の長さが $1,~\dfrac{\sqrt{3}}{2},~\dfrac{1}{2}$ の直角三角形を作ることができる。
- 直角三角形を作る必要はない。
三角比を含む不等式
以下の式を満たす $\theta$ を求めよ。ただし $0^\circ\leqq\theta\leqq180^\circ$ とする。
- $\cos\theta\leqq-\dfrac{\sqrt{3}}{2}$
- $\sin\theta\gt\dfrac{\sqrt{2}}{2}$
- $\tan\theta\gt-\sqrt{3}$
- 上半分の単位円周上において \[(x座標の値)\leqq-\dfrac{\sqrt{3}}{2}\] であればよい。そのようになるのは、図の太線部分であるので $\boldsymbol{150^\circ\leqq\theta\leqq180^\circ}$。

- 上半分の単位円周上において \[(y座標の値)\gt\dfrac{\sqrt{2}}{2}\] であればよい。そのようになるのは、図の太線部分であるので $\boldsymbol{45^\circ\lt\theta\lt135^\circ}$。

- 上半分の単位円周上において \[(動径の傾き)\gt-\sqrt{3}\] であればよい。そのようになるのは、図の太線部分であるので $\boldsymbol{0^\circ\leqq\theta\lt90^\circ,120^\circ\lt\theta\leqq180^\circ}$。
