三角形の面積と三角比
三角形の面積
$\triangle\text{ABC}$ の面積を、2辺の長さ $a$、$b$ と、その間の角度 $\theta$ を用いて表すことを考えてみよう。次の左の図は $\theta$ が鋭角の場合、次の右の図は $\theta$ が鈍角の場合を表している。
鋭角三角形
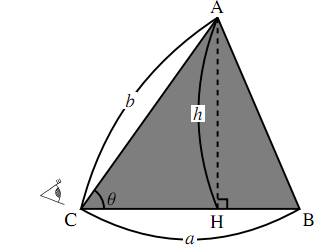
鈍角三角形
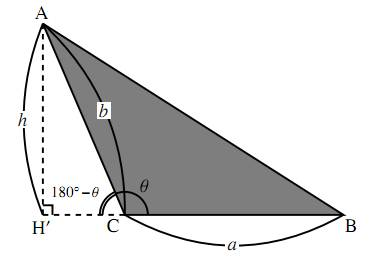
前の図の三角形において、底辺を $a$ とすれば高さは $h$ であるから、三角形の面積 $S$ はどちらも $S=\dfrac{ah}{2}$ である。
ここで高さ $h$ は、前の左の図では、$h=b\sin\theta$ であり、前の右の図でも \[h=b\sin(180^\circ-\theta)=b\sin\theta\] である。すなわち、鋭角三角形、鈍角三角形のどちらの場合でも、高さは $h=b\sin\theta$ となり \[S=\dfrac{ah}{2}=\dfrac{a{\cdot}b\sin\theta}{2}=\dfrac{1}{2}ab\sin\theta\] と表すことができる(これは、$\theta=90^\circ$ の直角三角形の場合も含んでいる)。
三角形の面積
三角形の面積
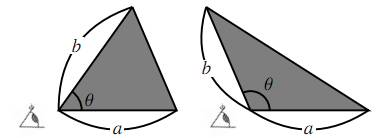
図の三角形の面積 $S$ は \[S=\dfrac{1}{2}ab\sin\theta\] で表せる。
吹き出し三角形の面積
$a$ を底辺とみれば $b\sin\theta$ が高さを表し、$b$ を底辺とみれば $a\sin\theta$ が高さを表す。