円と直線

円と直線の位置関係

円と直線の位置関係

円と直線の共有点の個数2個1個0個
円と直線の位置関係

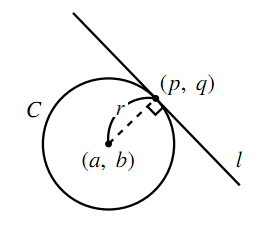
円と接線

円と接線

接弦定理

接弦定理

接弦定理

無題

無題

円の接線とその接点を通る弦の作る角は，その内部にある弧に対する円周角に等しい．

接弦定理

次の図で， $\text{AT}$ は円の接線であり， $\text{A}$ はその接点である． $\angle{x}$ の大きさを求めよ．

  1. $\angle{x}=65^\circ$
  2. $\angle{x}=58^\circ\times2=\boldsymbol{116^\circ}$
  3. $\angle{x}=180^\circ-(68^\circ+36^\circ)=\boldsymbol{76^\circ}$
  4. $(\angle{x}+55^\circ)+102^\circ=180^\circ,\angle{x}=\boldsymbol{23^\circ}$
  5. $\angle{\text{BAT}}=\angle{\text{ACB}}=\angle{\text{ACD}}=26^\circ$ ，

    6. $\angle{\text{ABD}}=\angle{\text{ACD}}=26^\circ$ より， $AT\parallel{DB}$

    \begin{align} \angle{x}&=\angle{\text{CAT}}\\ &=180^\circ-(26^\circ+62^\circ)\\ &=\boldsymbol{92^\circ} \end{align}

  6. $\angle{\text{ABD}}=28^\circ,\angle{\text{BAD}}=90^\circ$ ，

    7. $\angle{\text{ADB}}=\angle{x}+28^\circ$ より，

    \begin{align} &28^\circ+90^\circ+(\angle{x}+28^\circ)=180^\circ,\\ &\angle{x}=\boldsymbol{34^\circ} \end{align}

方べきの定理

方べきの定理

方べきの定理

方べきの定理には，主に次の2つがある．

  1. 1つの円における2つの弦 $\mathrm{AB},\mathrm{CD}$ の交点，またはそれらの延長の交点を $\mathrm{P}$ とすると，
    2. \[\mathrm{PA}\cdot\mathrm{PB}=\mathrm{PC}\cdot\mathrm{PD}\]

    が成り立つ．

  2. 円の外部の点 $\mathrm{P}$ から円に引いた接線の接点を $\mathrm{T}$ とする． $\mathrm{P}$ を通ってこの円と2点 $\mathrm{A},\mathrm{B}$ で交わる直線を引くと，
    3. \[\mathrm{PA}\cdot\mathrm{PB}=\mathrm{PT}^2\]

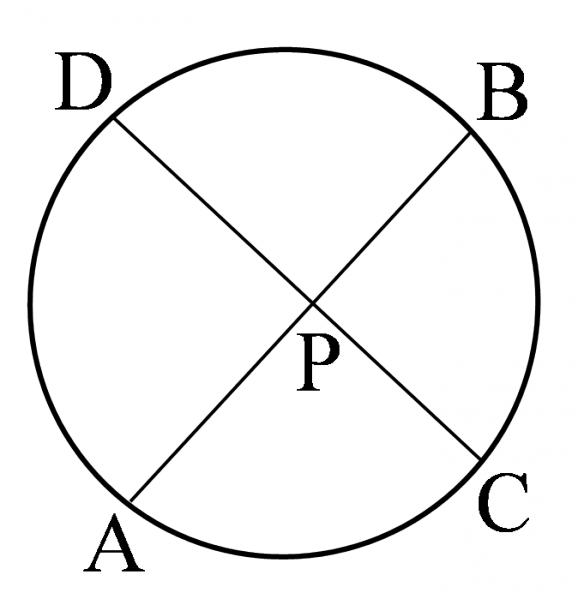
    が成り立つ．

方べきの定理

次の図において， $x$ の値を求めよ．ただし，Tは円の接点とする．

  1. $4\cdot4=8x$ ， $\boldsymbol{x=2}$
  2. $(x+6)\cdot{x}=5\cdot8,x^2+6x-40=0$

    3. $x\gt0$ より， $\boldsymbol{x=4}$

  3. $6\cdot10=x^2$

    4. $x\gt0$ より， $\boldsymbol{x=2\sqrt{15}}$