円と円
2円の位置関係
2円の位置関係
2円の位置関係は,2円の半径と中心間の距離で決まり,以下の5つの状態がある.
2円の位置関係
2円の半径を $r_1,r_2(r_1\lt r_2)$ ,中心間の距離を $d$ とすると,以下のようになる.
| 2円の図 |  |  |  | |
| 2円の位置関係 | 離れている | 外接している | 交わっている | |
| 2円の共有点の個数 | 0個 | 1個(外接) | 2個 | |
| 2円の中心間の距離 $d$ | $d\gt{r_1+r_2}$ | $d=r_1+r_2$ | $d\lt{r_1+r_2}$ |
| 2円の図 |  |  | |
| 2円の位置関係 | 内接している | 一方が他方を含む | |
| 2円の共有点の個数 | 1個(内接) | 0個 | |
| 2円の中心間の距離 $d$ | $d\gt{r_2-r_1}$ | $d\lt{r_2-r_1}$ |
2円の関係
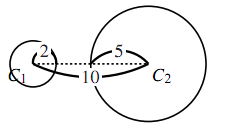
円 $C_1$ は $\text{A}$ を中心とした半径 $2$ の円,円 $C_2$ は $\text{B}$ を中心とした半径 $5$ の円とする.
- $\text{AB}=10$ のとき,円 $C_1$ と $C_2$ はどんな位置関係にあるか.また, $\text{AB}=6$ のとき, $\text{AB}=2$ のときはどうか.
- $C_1$ と $C_2$ が外接するとき線分 $\text{AB}$ の長さを求めよ.また,内接するときはどうか.
- $C_1$ が $C_2$ に含まれるための,線分 $\text{AB}$ の長さの条件を求めよ.
- $\text{AB}=10$ のときは共有点がない
- 外接のときは $\text{AB}=7$ ,内接のときは $\text{AB}=3$ .
- 線分 $\text{AB}$ の長さが,内接するときより短ければよいので, $(0\lt)\boldsymbol{\text{AB}\lt3}$ .
$\text{AB}=6$ のときは2点で交わる
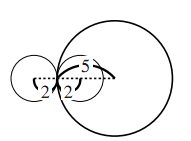
$\text{AB}=2$ のときは円 $C_1$ が円 $C_2$ に含まれている
2円と共通接線
2円と共通接線
2円の共通接線の本数は,2円の位置関係によって異なる.
2円の共通接線
| 共通接線の本数 | 4本 | 3本 | 2本 | 1本 | 0本 | |
| 2円と共通接線の図 |  |  |  |  |  | |
| 2円の位置関係 | 離れている | 外接している | 交わっている | 内接している | 一方が他方を含む |
$\uparrow$ 2円の中心間を横切る共通接線は共通内接線(2本ある),2円の上下で接する共通接線は共通外接線(2本ある)と言われる.
共通接線の方程式を求めるには,問題を図示し,図形的に考えることが不可欠である.
2円と共通接線
次の図で,直線 $\text{AB}$ は円 $\text{O}$ , $\text{O'}$ の共通接線で, $\text{A}$ , $\text{B}$ はその接点である.このとき,点 $\text{O'}$ から直線 $\text{OA}$ に垂線 $\text{O'A'}$ を引き, $\triangle{\mathrm{OO'A'}}$ を考えることにより,線分 $\text{AB}$ の長さを求めよ.
- \[\sqrt{13^2-(10-5)^2}=\boldsymbol{12}\]
- \[\sqrt{15^2-(8+4)^2}=\boldsymbol{9}\]

