弧度法

度数法の問題点

（注） （注）

度数法の問題点

これまで，角度の大きさは「1周は$360^\circ$」と定義して表してきた． この方法は度数法(degree measure) と呼ばれ， 紀元前から用いられてきたものである． しかし，度数法で表わされた角の値は便宜的なもので数学的根拠がなく， 数学の発展と共に不便が生じてきた．

弧度法の定義

弧度法の定義

そこで，これらの不便を解消するための新しい角度を導入しよう．

弧度法

無題

無題 （注）

弧の長さが$l$,半径が$r$の円弧のなす中心角$\theta$を

\begin{align} \theta=\dfrac{l}{r} \end{align}

で定義する．

このような角度の表し方を弧度法(circular measure) という． 弧度法は比で角度の大きさを表すため，単位が無いが，あえて単位を付けたいときにはラジアン(radian) や弧度をもちいる．

無題

無題

上の定義において，$r = 1$とすると$\theta = l$となる． これは，単位円で考えたときには，中心角は対応する弧の長さで表されることを意味している． すなわち

\begin{align} 360^\circ=2\pi \end{align}ラジアン

である．

主な角について，度数法と弧度法の値をまとめると次のようになる．

度数法$0^\circ$$30^\circ$$45^\circ$$60^\circ$$90^\circ$$120^\circ$
弧度法$0$$\dfrac{\pi}{6}$$\dfrac{\pi}{4}$$\dfrac{\pi}{3}$$\dfrac{\pi}{2}$$\dfrac{2}{3}\pi$

度数法$135^\circ$$150^\circ$$180^\circ$$270^\circ$$360^\circ$
弧度法$\dfrac{3}{4}\pi$$\dfrac{5}{6}\pi$$\pi$$\dfrac{3}{2}\pi$$2\pi$

弧度法についても動径の表す角について，次のことがいえる．

弧度法での動径の表す角

動径$\text{OP}$と始線$\text{OX}$のなす角の1つを$\alpha$とすると，動径$\text{OP}$の表す角$\theta$は

\begin{align} \theta=\alpha+2n\pi \end{align}($n$は整数)

のようにあらわされる．

度数法を弧度法になおす

次の角を弧度法で表せ．また，$\alpha + 2n \pi $($n$は整数)の形で表せ．ただし，$0\leqq\alpha<2\pi$とする．

  1. $15^\circ$
  2. $550^\circ$
  3. $80^\circ$
  4. $-570^\circ$

  1. $\boldsymbol{\dfrac{\pi}{12}},\boldsymbol{\dfrac{\pi}{12}+2n\pi}$
  2. $\boldsymbol{\dfrac{55}{18}\pi},\boldsymbol{\dfrac{19}{18}\pi+2n\pi}$
  3. $\boldsymbol{\dfrac{4}{9}\pi},\boldsymbol{\dfrac{4}{9}\pi+2n\pi}$
  4. $\boldsymbol{-\dfrac{19}{6}\pi},\boldsymbol{\dfrac{5}{6}\pi+2n\pi}$

弧度法を度数法になおす

次の角を度数法で表せ．

  1. $8\pi$
  2. $-\dfrac{7}{3}\pi$
  3. $-\dfrac{43}{12}\pi$
  4. $-\dfrac{21}{10}\pi$

  1. $\boldsymbol{1440^\circ}$
  2. $\boldsymbol{-420^\circ}$
  3. $\boldsymbol{-645^\circ}$
  4. $\boldsymbol{-378^\circ}$

扇形の弧の長さと面積

無題

無題

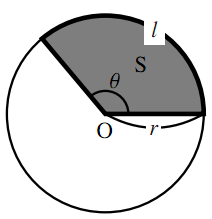
扇形の弧の長さと面積

扇形の弧の長さと面積を，弧度法をもちいて表してみよう．

図のように半径が$r$,中心角が$\theta$の扇形の弧の長さを$l$,面積を$\text{S}$とすると，弧度法の定義より$\theta=\dfrac{l}{r}$だから

\begin{align} \therefore~&l=r\theta \end{align} $\tag{1}\label{ougigatanokononagasatomenseki1}$

面積と中心角の比から

\begin{align} \qquad{\text{S}}:\theta=\pi r^2:2\pi \end{align} \begin{align} \therefore~&\text{S}=\dfrac{1}{2}r^2\theta \end{align} $\tag{2}\label{ougigatanokononagasatomenseki2}$

以上，$\eqref{ougigatanokononagasatomenseki1}$，$\eqref{ougigatanokononagasatomenseki2}$より，$\text{S}=\dfrac{1}{2}rl$となる．

扇形の弧の長さと面積

無題

無題

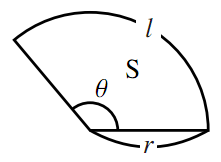
半径が$r$,中心角が$\theta$の扇形の弧の長さを$l$,面積を$\text{S}$とすると

\begin{align} &l=r\theta\\ &\text{S}=\dfrac{1}{2}r^2\theta=\dfrac{1}{2}rl \end{align}

である．

吹き出し扇形の弧の長さと面積

無題

無題

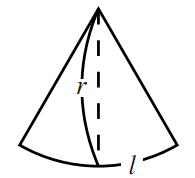
図のように，扇形を，あたかも底辺が$l$,高さが$r$の三角形のように考え， (底辺)$\times$(高さ)$\div 2$から，$\text{S}=\dfrac{1}{2}rl$と覚えておけばよい．

扇形の弧の長さと面積

次のような扇形の弧の長さ$l$と面積$\text{S}$を求めよ．

  1. 半径が$9$，中心角が$\dfrac{2}{3}\pi$
  2. 半径が$3$，中心角が$\dfrac{\pi}{5}$

  1. $l=9\times\dfrac{2}{3}\pi=\boldsymbol{6\pi},$
    $\text{S}=\dfrac{1}{2}\times9\times6\pi=\boldsymbol{27\pi}$
  2. $l=3\times\dfrac{\pi}{5}=\boldsymbol{\dfrac{3}{5}\pi},$
    $\text{S}=\dfrac{1}{2}\times3\times\dfrac{3}{5}\pi=\boldsymbol{\dfrac{9}{10}\pi}$