正弦と余弦の加法定理

正弦と余弦の加法定理

2つの角の和や差の三角関数は，それぞれの角の三角関数で表すことができる． まずはじめに

\begin{align} \cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta \end{align} $\tag{1}\label{seigentoyogennokahouteiri1}$

となることを証明してみよう．

【証明】

図のように，点$\text{P}(\cos\alpha,~\sin\alpha)$と点$\text{Q}(\cos\beta,~\sin\beta)$をとると， 2点間の距離の公式より

\begin{align} \text{PQ}^2&=(\cos\beta-\cos\alpha)^2+(\sin\beta-\sin\alpha)^2\\ &=2-2(\cos\alpha\cos\beta+\sin\alpha\sin\beta) \end{align}

である．

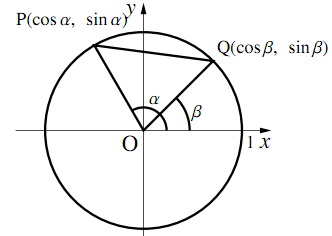
正弦と余弦の加法定理の図その１

次に，図のように，2点$\text{P}，\text{Q}$を原点を中心に$ − \beta$だけ回転させた図形を考える． このとき，動径$\text{OP}$のなす角は$\alpha − \beta$となるので，2点間の距離の公式より

\begin{align} \text{PQ}^2&=(1-\cos(\alpha-\beta))^2+\sin^2(\alpha-\beta)\\ &=2-2\cos(\alpha-\beta) \end{align}

よって

\begin{align} &2-2(\cos\alpha\cos\beta+\sin\alpha\sin\beta)\\ &=2-2\cos(\alpha-\beta)\\ \Leftrightarrow~&\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta \end{align}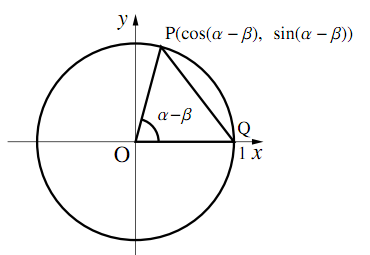
正弦と余弦の加法定理の図その２

暗記正弦と余弦の加法定理の導出

上の$\eqref{seigentoyogennokahouteiri1}$を利用して，次の等式を証明せよ．

  1. $\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$
  2. $\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta$
  3. $\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$

  1. $\eqref{seigentoyogennokahouteiri1}$で$\beta$を $− \beta$におきかえると

    \begin{align} &\cos\{\alpha-(-\beta)\}=\cos\alpha\cos(-\beta)\\ &\qquad\qquad\qquad+\sin\alpha\sin(-\beta)\\ \Leftrightarrow~&\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta \end{align}

    ← $-\theta$の三角比

  2. $\eqref{seigentoyogennokahouteiri1}$で$\beta$を$\beta-\dfrac{\pi}{2}$におきかえると

    \begin{align} &\cos\left\{\alpha-\left(\beta-\dfrac{\pi}{2}\right)\right\}\\ &\qquad=\cos\alpha\cos\left(\beta-\dfrac{\pi}{2}\right)\\ &\qquad+\sin\alpha\sin\left(\beta-\dfrac{\pi}{2}\right)\\ \Leftrightarrow~&\cos\left\{(\alpha-\beta)+\dfrac{\pi}{2}\right\}\\ &\qquad=\cos\alpha\cos\left(\beta-\dfrac{\pi}{2}\right)\\ &\qquad+\sin\alpha\sin\left(\beta-\dfrac{\pi}{2}\right)\\ \Leftrightarrow~&-\sin(\alpha-\beta)=\cos\alpha\sin\beta-\sin\alpha\cos\beta\\ \Leftrightarrow~&\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta \end{align}

  3. 2.で$\beta$を$ − \beta$におきかえると

    \begin{align} &\sin\left\{\alpha-(-\beta)\right\}=\sin\alpha\cos(-\beta)\\ &\qquad\qquad\qquad-\cos\alpha\sin(-\beta)\\ &\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta \end{align}

    ← $-\theta$の三角比

正弦と余弦の加法定理

\begin{align} 1)&\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\\ &\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta\\ 2)&\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\\ &\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta \end{align}

正弦と余弦の加法定理

  1. $45^\circ-30^\circ=15^\circ$であることに注意して，$\sin15^\circ$と$\cos15^\circ$の値を求めよ．

  2. $\dfrac{\pi}{4}+\dfrac{\pi}{6}=\dfrac{5}{12}\pi$であることに注意して$\sin\dfrac{5}{12}\pi$と$\cos\dfrac{5}{12}\pi$の値を求めよ．

  1. 加法定理をもちいて

    \begin{align} \sin15^\circ&=\sin(45^\circ-30^\circ)\\ &=\sin45^\circ\cos30^\circ-\cos45^\circ\sin30^\circ\\ &=\dfrac{\sqrt{2}}{2}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{2}\cdot\dfrac{1}{2}\\ &=\boldsymbol{\dfrac{\sqrt{6}-\sqrt{2}}{4}}\\ \cos15^\circ&=\cos(45^\circ-30^\circ)\\ &=\cos45^\circ\cos30^\circ+\sin45^\circ\sin30^\circ\\ &=\dfrac{\sqrt{2}}{2}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{2}\cdot\dfrac{1}{2}\\ &=\boldsymbol{\dfrac{\sqrt{6}+\sqrt{2}}{4}} \end{align}

  2. 加法定理をもちいて

    \begin{align} \sin\dfrac{5}{12}\pi&=\sin\left(\dfrac{\pi}{4}+\dfrac{\pi}{6}\right)\\ &=\sin\dfrac{\pi}{4}\cos\dfrac{\pi}{6}+\sin\dfrac{\pi}{4}\cos\dfrac{\pi}{6}\\ &=\dfrac{\sqrt{2}}{2}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{2}\cdot\dfrac{1}{2}\\ &=\boldsymbol{\dfrac{\sqrt{6}+\sqrt{2}}{4}}\\ \cos\dfrac{5}{12}\pi&=\cos\left(\dfrac{\pi}{4}+\dfrac{\pi}{6}\right)\\ &=\cos\dfrac{\pi}{4}\cos\dfrac{\pi}{6}-\sin\dfrac{\pi}{4}\sin\dfrac{\pi}{6}\\ &=\dfrac{\sqrt{2}}{2}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{2}\cdot\dfrac{1}{2}\\ &=\boldsymbol{\dfrac{\sqrt{6}-\sqrt{2}}{4}} \end{align}

三角関数の加法定理と平面図形

無題

無題

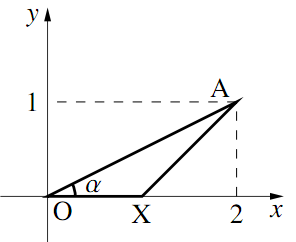
図のように$\text{X}(1,~0)$と$\text{A}(2,~1)$があり，$\angle{\text{AOX}}=\alpha$とする．

  1. $\cos\alpha,~\sin\alpha$の値を求めよ．

  2. $\triangle{\text{AOX}}$を$\text{O}$を中心に$\dfrac{\pi}{3}$回転移動し，$\triangle{\text{A}'\text{OX}'}$になったとする． このとき，$\text{X}'$，$\text{A}'$の座標を求めよ．

  1. $\text{OA}=\sqrt{5}$より，

    $\boldsymbol{\cos\alpha=\dfrac{2}{\sqrt{5}},~\sin\alpha=\dfrac{1}{\sqrt{5}}}$．

  2. 図のように書くことができ，

    三角関数の加法定理と平面図形の解答の図その１

    $ \text{X}'\left(\cos\dfrac{\pi}{3},~\sin\dfrac{\pi}{3}\right)$なので$\boldsymbol{ \text{X}'\left(\dfrac12,~\dfrac{\sqrt{3}}{2}\right)}$．

    $ \text{A}'\left(\sqrt{5}\cos\left(\alpha+\dfrac{\pi}{3}\right),~\sqrt{5}\sin\left(\alpha+\dfrac{\pi}{3}\right)\right)$であり，

    \begin{align} &\cos\left(\alpha+\dfrac{\pi}{3}\right)=\cos\alpha\cos\dfrac{\pi}{3}-\sin\alpha\sin\dfrac{\pi}{3}\\ &=\dfrac{2}{\sqrt{5}}\cdot\dfrac12 - \dfrac{1}{\sqrt{5}}\cdot\dfrac{\sqrt{3}}{2} =\dfrac{2-\sqrt{3}}{2\sqrt{5}}\\ &\sin\left(\alpha+\dfrac{\pi}{3}\right)=\sin\alpha\cos\dfrac{\pi}{3}+\cos\alpha\sin\dfrac{\pi}{3}\\ &=\dfrac{1}{\sqrt{5}}\cdot\dfrac12 + \dfrac{2}{\sqrt{5}}\cdot\dfrac{\sqrt{3}}{2} =\dfrac{1+2\sqrt{3}}{2\sqrt{5}} \end{align}

    ← 正弦と余弦の加法定理

    より，$\boldsymbol{ \text{A}'\left(\dfrac{2-\sqrt{3}}{2},~\dfrac{1+2\sqrt{3}}{2}\right)}$．

    ←$\cos\left(\alpha+\dfrac{\pi}{3}\right),~\sin\left(\alpha+\dfrac{\pi}{3}\right)$をそれぞれ$\sqrt{5}$倍した