2直線のなす角

正接の加法定理を利用すると，2直線のなす角の正接の値を求めることができる．そのことを次の例題で確認しよう．

2直線のなす角〜その1〜

直線$l:y=2x-1,m:y=\dfrac{1}{3}x+\dfrac{1}{3}$について，以下の問いに答えよ．

直線$l,m$が$x$軸の正の向きとなす角を$\alpha,\beta$とするとき，$\tan\alpha,\tan\beta$の値を求めよ．ただし，角は反時計回りを正の向きとする．
2直線$l,m$のなす鋭角を$\theta$とする．正接の加法定理を利用し$\theta$の値を求めよ．

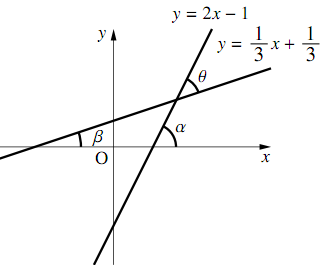
直線$l$と$m$の傾きはそれぞれ，$2,\dfrac{1}{3}$なので，
$\tan\alpha=\boldsymbol{2},\tan\beta=\boldsymbol{\dfrac{1}{3}}$である．
$\theta = \beta − \alpha$なので
\begin{align} &\tan\theta\\ &=\tan(\alpha-\beta)\\ &=\dfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}\\ &=\dfrac{2-\dfrac{1}{3}}{1+2\cdot\dfrac{1}{3}}\\ &=1 \end{align}
$0\leqq\theta\leqq\dfrac{\pi}{2}$より，$\theta=\boldsymbol{\dfrac{\pi}{4}}$となる．

以下では，交わる2直線$y=m_1x+n_1,y=m_2x+n_2$のなす鋭角$\theta$について，一般的に考えてみよう．

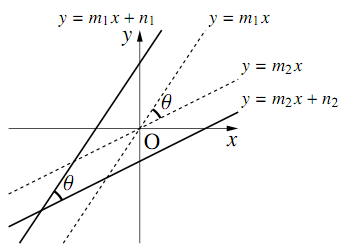
図のように，直線を平行移動しても2直線のなす角は変わらないので，$y=m_1x,y=m_2x$の場合について考えてゆけばよい．

直線$y=m_1 x,~y=m_2 x$が$x$軸の正の向きとなす，正の角をそれぞれ$\alpha,\beta~(\alpha>\beta)$とする．

正接の値は直線の傾きを表していたので，$\tan\alpha=m_1,~\tan\beta=m_2$である．

いま，正接の加法定理から

\begin{align} \tan(\alpha-\beta)&=\dfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}=\dfrac{m_1-m_2}{1+m_1m_2} \end{align}

と計算できる．

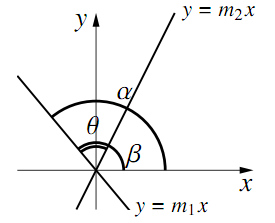
$\dfrac{m_1-m_2}{1+m_1m_2}>0$,すなわち$0<\alpha-\beta <\dfrac{\pi}{2}$のとき
\begin{align} \tan\theta=\tan(\alpha-\beta)=\dfrac{m_1-m_2}{1+m_1m_2}~(>0) \end{align}
$\dfrac{m_1-m_2}{1+m_1m_2}<0$,すなわち$\dfrac{\pi}{2}<\alpha-\beta<\pi$のとき
\begin{align} \tan\theta&=\tan\left\{\pi-(\alpha-\beta)\right\}\\ &=-\tan(\alpha-\beta)\\ &=-\dfrac{m_1-m_2}{1+m_1m_2}~(>0) \end{align}
いずれにしても，$\tan\theta > 0$なので，次のようにまとめられる．

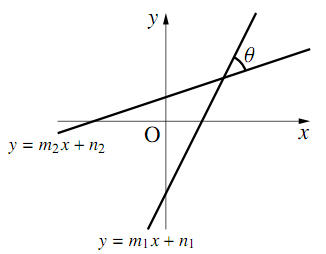
直交しない2直線

\begin{align} &y=m_1x+n_1~~~~~y=m_2x+n_2 \end{align}

のなす鋭角を$\theta$とすると

\begin{align} \tan\theta=\left|\dfrac{m_1-m_2}{1+m_1m_2}\right| \end{align}

と表すことができる．

それぞれ傾きは$2,~-1$なので
\begin{align} \tan\theta =\left|\dfrac{2 -(-1)}{1+2\cdot (-1)}\right| =|-3| =\boldsymbol{3} \end{align}
傾きは$2,~m$である2直線のなす角が$\dfrac{\pi}{4}$なので
\begin{align} \tan\dfrac{\pi}{4}=\left|\dfrac{2 -m}{1+2\cdot m}\right| \Leftrightarrow~ &1=\left|\dfrac{2-m}{2m+1}\right| \end{align}
よって，$2m+1=2-m$または$2m+1=m-2$であればよいので， $\boldsymbol{m=\dfrac{1}{3},~-3}$．