三角比の値のまとめ
角度が $0^\circ$、$30^\circ$、$45^\circ$、$60^\circ$、$90^\circ$、$120^\circ$、$135^\circ$、$150^\circ$、$180^\circ$ の場合の三角比は、頭の中で次のような図を思い描き、素早く求められるようになろう。
$0^\circ\leqq\theta\leqq180^\circ$ までの三角比
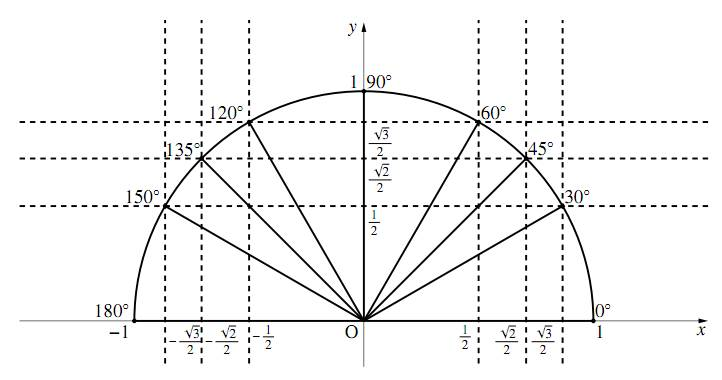
有名角の三角比
上の図をもとに下の表を完成させよ。
| $\theta$ | | $0^\circ$ | $30^\circ$ | $45^\circ$ | $60^\circ$ | $90^\circ$ | $120^\circ$ | $135^\circ$ | $150^\circ$ | $180^\circ$ |
| | | | | | | | | | |
| $\sin\theta$ | | | | | | | | | | |
| $\cos\theta$ | | | | | | | | | | |
| $\tan\theta$ | | | | | | | | | | |
| $\theta$ | | $0^\circ$ | $30^\circ$ | $45^\circ$ | $60^\circ$ | $90^\circ$ |
| | | | | | |
| $\sin\theta$ | | $0$ | $\dfrac{1}{2}$ | $\dfrac{\sqrt{2}}{2}$ | $\dfrac{\sqrt{3}}{2}$ | $1$ |
| $\cos\theta$ | | $1$ | $\dfrac{\sqrt{3}}{2}$ | $\dfrac{\sqrt{2}}{2}$ | $\dfrac{1}{2}$ | $0$ |
| $\tan\theta$ | | $0$ | $\dfrac{1}{\sqrt{3}}$ | $1$ | $\sqrt{3}$ | なし |
| $\theta$ | | $120^\circ$ | $135^\circ$ | $150^\circ$ | $180^\circ$ |
| | | | | |
| $\sin\theta$ | | $\dfrac{\sqrt{3}}{2}$ | $\dfrac{\sqrt{2}}{2}$ | $\dfrac{1}{2}$ | $0$ |
| $\cos\theta$ | | $-\dfrac{1}{2}$ | $-\dfrac{\sqrt{2}}{2}$ | $-\dfrac{\sqrt{3}}{2}$ | $-1$ |
| $\tan\theta$ | | $-\sqrt{3}$ | $-1$ | $-\dfrac{1}{\sqrt{3}}$ | $0$ |
