拡張された三角比の相互関係について
拡張された三角比においても、三角比の相互関係で学んだ三角比の相互関係 \begin{align} &\tan\theta=\dfrac{\sin\theta}{\cos\theta},~\sin^2\theta+\cos^2\theta=1\\ &1+\dfrac{1}{\tan^2\theta}=\dfrac{1}{\sin^2\theta},~\tan^2\theta+1=\dfrac{1}{\cos^2\theta} \end{align} が成り立つ。以下でこれらのことを確認してみよう。
拡張された三角比の相互関係
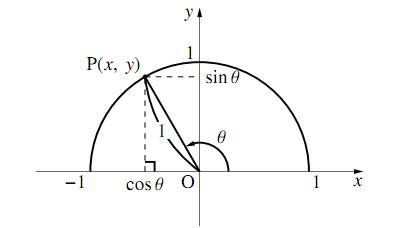
図の単位円において \[\cos\theta=x~,~\sin\theta=y\] であるから、$\tan\theta$ は \[\tan{\theta}=\dfrac{y}{x}=\dfrac{\sin\theta}{\cos\theta}\] と表すことができる。つまり \[\tan\theta=\dfrac{\sin\theta}{\cos\theta}\tag{1}\label{kakutyosaretasankakuhinosougokankenituite1}\] が成り立つ。また、三平方の定理より、$x^2+y^2=1$ であるから \[\sin^2\theta+\cos^2\theta=1\tag{2}\label{kakutyosaretasankakuhinosougokankenituite2}\] が成り立ち、$\eqref{kakutyosaretasankakuhinosougokankenituite2}$ の両辺を $\sin^2\theta$ で割って、$\tan\theta=\dfrac{\sin\theta}{\cos\theta}$ を用いると \begin{align} &1+\dfrac{\cos^2\theta}{\sin^2\theta}=\dfrac{1}{\sin^2\theta}\\ \therefore~~&1+\dfrac{1}{\tan^2\theta}=\dfrac{1}{\sin^2\theta}\tag{3}\label{kakutyosaretasankakuhinosougokankenituite3} \end{align} また、$\eqref{kakutyosaretasankakuhinosougokankenituite2}$ の両辺を $\cos^2\theta$ で割って、$\tan\theta=\dfrac{\sin\theta}{\cos\theta}$ を用いると \begin{align} &\dfrac{\sin^2\theta}{\cos^2\theta}+1=\dfrac{1}{\cos^2\theta}\\ \therefore~~&\tan^2\theta+1=\dfrac{1}{\cos^2\theta}\tag{4}\label{kakutyosaretasankakuhinosougokankenituite4} \end{align}
拡張された三角比の相互関係
角 $\theta$ が $0^\circ\leqq\theta\leqq180^\circ$ のとき、次の式が成り立つ。
- $\sin\theta$、$\cos\theta$、$\tan\theta$ の関係 \[\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}\]
- $\sin\theta$ と $\cos\theta$ の関係 \[\sin^2{\theta}+\cos^2{\theta}=1\]
- $\tan\theta$ と $\sin\theta$ の関係 \[1+\dfrac{1}{\tan^2{\theta}}=\dfrac{1}{\sin^2{\theta}}\]
- $\cos\theta$ と $\tan\theta$ の関係 \[\tan^2{\theta}+1=\dfrac{1}{\cos^2{\theta}}\]
三角比どうしの関係と同じ問を、拡張された三角比の相互関係を使って解いてみよう。ただし、今回は $0^\circ$ から $180^\circ$ までの範囲で考える。
拡張された三角比の相互関係の利用
拡張された三角比の相互関係を使って次の問に答えよ。ただし $0^\circ\leqq\alpha\leqq 180^\circ$ である。
- $\sin\alpha=\dfrac{3}{5}$ のとき、$\cos\alpha$、$\tan\alpha$ の値を求めよ。
- $\cos\alpha=\dfrac{1}{3}$ のとき、$\sin\alpha$、$\tan\alpha$ の値を求めよ。
- $\tan\alpha=7$ のとき、$\cos\alpha$、$\sin\alpha$ の値を求めよ。
- $\blacktriangleleft$ 拡張された三角比の相互関係より$\sin^2\alpha+\cos^2\alpha=1$ \begin{align} \cos^2\alpha=1-\sin^2\alpha=1-\left(\dfrac{3}{5}\right)^2=\dfrac{16}{25} \end{align} よって、$\cos\alpha=\pm\sqrt{\dfrac{16}{25}}=\boldsymbol{\pm\dfrac{4}{5}}$。$\blacktriangleleft$ 拡張された三角比の相互関係よりまた、$\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}$ より、$\blacktriangleleft$ $\cos\alpha=\pm\dfrac{4}{5},~\tan\alpha=\pm\dfrac{3}{4}$(複合同順)と書いてもよい\begin{align} &\cos\alpha=\dfrac{4}{5}のとき\tan\alpha=\dfrac{\dfrac{3}{5}}{\dfrac{4}{5}}=\boldsymbol{\dfrac{3}{4}}\\ &\cos\alpha=-\dfrac{4}{5}のとき\\ &\tan\alpha=\dfrac{\dfrac{3}{5}}{-\dfrac{4}{5}}=\boldsymbol{-\dfrac{3}{4}} \end{align}
- $\blacktriangleleft$ 拡張された三角比の相互関係より$\sin^2\alpha+\cos^2\alpha=1$ より \begin{align} \sin^2\alpha=1-\cos^2\alpha=1-\left(\dfrac{1}{3}\right)^2=\dfrac{8}{9} \end{align}$\blacktriangleleft$ $0^\circ\leqq\alpha\leqq180^\circ$ のとき、定義から $\sin\alpha\geqq0$。$\sin\alpha\geqq0$ なので、$\sin\alpha=\sqrt{\dfrac{8}{9}}=\boldsymbol{\dfrac{2\sqrt{2}}{3}}$。$\blacktriangleleft$ 拡張された三角比の相互関係よりまた、$\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}$ より \begin{align} \tan\alpha=\dfrac{\dfrac{2\sqrt{2}}{3}}{\dfrac{1}{3}}=\boldsymbol{2\sqrt{2}} \end{align}
- $\blacktriangleleft$ 拡張された三角比の相互関係より$\tan^2\alpha+1=\dfrac{1}{\cos^2\alpha}$ より \begin{align} \cos^2\alpha=\dfrac{1}{1+\tan^2\alpha}=\dfrac{1}{1+7^2}=\dfrac{1}{50} \end{align} よって、$\cos\alpha=\pm\sqrt{\dfrac{1}{50}}=\pm\dfrac{\sqrt{2}}{10}$ である。$\blacktriangleleft$ 拡張された三角比の相互関係よりまた、$\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}$ より \begin{align} &7=\dfrac{\sin\alpha}{\pm\dfrac{\sqrt{2}}{10}}\\ \therefore~~&\sin\alpha=7\times\left(\pm\dfrac{\sqrt{2}}{10}\right)=\pm\dfrac{7\sqrt{2}}{10} \end{align}$\blacktriangleleft$ $\tan\alpha$ の値が正であるから、$\cos\alpha$ の値も正である$0\leqq\sin\alpha$ であるので、$\sin\alpha=-\dfrac{7\sqrt{2}}{10}$ は不適。
よって \[\boldsymbol{\cos\alpha=\dfrac{\sqrt{2}}{10}~,~\sin\alpha=\dfrac{7\sqrt{2}}{10}}\]
三角比の計算
次の式を簡単にせよ。
- $(\sin\theta+\cos\theta)^2+(\sin\theta-\cos\theta)^2$
- $\dfrac{\cos\theta}{1+\sin\theta}-\dfrac{\cos\theta}{1-\sin\theta}$
- $\blacktriangleleft$ 拡張された三角比の相互関係より\begin{align} &(\sin \theta+\cos\theta)^2+(\sin\theta-\cos\theta)^2\\ =&\sin^2\theta+2\sin\theta\cos\theta+\cos^2\theta\\ &\qquad+\sin^2\theta -2\sin\theta\cos\theta+\cos^2\theta\\ =&2(\sin^2\theta+\cos^2\theta)\\ =&\boldsymbol{2} \end{align}
- $\blacktriangleleft$ 拡張された三角比の相互関係より\begin{align} &\dfrac{\cos\theta}{1+\sin\theta}-\dfrac{\cos\theta}{1-\sin\theta}\\ =&\dfrac{\cos\theta\left(1-\sin\theta\right)-\cos\theta\left(1+\sin\theta\right)} {\left(1+\sin\theta\right)\left(1-\sin\theta\right)}\\ =&\dfrac{-2\cos\theta\sin\theta}{1-\sin^2\theta}\\ =&-\dfrac{2\cos\theta\sin\theta}{\cos^2\theta}\\ =&-\dfrac{2\sin\theta}{\cos\theta}\\ =&\boldsymbol{-2\tan\theta} \end{align}