パスカルの三角形
図のように,2項係数 $_{n}\mathrm{C}_{0},\ _{n}\mathrm{C}_{1},\ _{n}\mathrm{C}_{2},\cdots,\ _{n}\mathrm{C}_{n}$ の値を,上から順に $n=1,2,3,\cdots$ の場合について三角形の形に並べたものを,パスカルの三角形(Pascal's triangle)という.

パスカルの三角形には,次のような特徴がある.
- $_{n}\mathrm{C}_{0}=\ _{n}\mathrm{C}_{n}=1$ であるから,各行の左右両端の数字は1である.
- $_{n}\mathrm{C}_{r}=\ _{n}\mathrm{C}_{n−r}$ であるから,各行は左右対称である.
- $_{n}\mathrm{C}_{r}=\ _{n−1}\mathrm{C}_{r-1}+\ _{n−1}\mathrm{C}_{r}$ であるから $_{n}\mathrm{C}_{r}$ の性質,左右両端以外の数字は,その左上の数と右上の数を足したものとなる.
パスカルの三角形
パスカルの三角形を利用して,次の展開式を求めよ.
- $(x+y)^6$
- $(x−2y)^5$
- パスカルの三角形を $n=6$ の場合まで書くと,図のようになるので
- パスカルの三角形を $n=5$ の場合まで書くと,図のようになるので
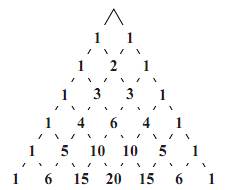 \begin{align}
&\ (x+y)^6\\
=&\ \boldsymbol{x^6+6x^5y+15x^4y^2+20x^3y^3}\\
&\ \qquad\qquad\boldsymbol{+15x^2y^4+6xy^5+y^6}
\end{align}
\begin{align}
&\ (x+y)^6\\
=&\ \boldsymbol{x^6+6x^5y+15x^4y^2+20x^3y^3}\\
&\ \qquad\qquad\boldsymbol{+15x^2y^4+6xy^5+y^6}
\end{align}
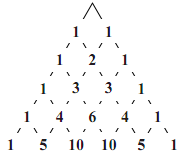 \begin{align}
&\ (x-2y)^5\\
=&\ x^5+5x^4(-2y)+10x^3(-2y)^2\\
&\ +10x^2(-2y)^3+5x(-2y)^4+(-2y)^5\\
=&\ \boldsymbol{x^5-10x^4y+40x^3y^2}\\
&\ \boldsymbol{-80x^2y^3+80xy^4-32y^5}
\end{align}
\begin{align}
&\ (x-2y)^5\\
=&\ x^5+5x^4(-2y)+10x^3(-2y)^2\\
&\ +10x^2(-2y)^3+5x(-2y)^4+(-2y)^5\\
=&\ \boldsymbol{x^5-10x^4y+40x^3y^2}\\
&\ \boldsymbol{-80x^2y^3+80xy^4-32y^5}
\end{align}