内分と外分
内分と外分
内分
説明文
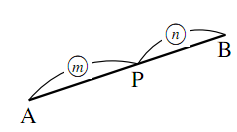
正の数 $m,n$ とする.線分 $\text{AB}$ 上の点 $\text{P}$ について
\[AP:PB=m:n\]が成り立つとき,点 $\text{P}$ は線分 $\text{AB}$ を $m:n$ に
内分(interior devision)
するといい, 点 $\text{P}$ のことを内分点という.
外分
正の数 $m,n$ とする.線分ABの延長上の点 $\text{Q}$ について
\[AQ:QB=m : n\]が成り立つとき,点 $\text{Q}$ は線分 $\text{AB}$ を $m:n$ に
外分(exterior devision)
するといい,点 $\text{Q}$ のことを外分点という.
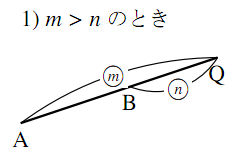
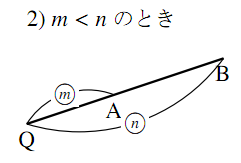
下図のように,点 $\text{Q}$ は
- $m\gt n$ のときは,線分 $\text{AB}$ の $\text{B}$ の方向への延長上
- $m\lt n$ のときは,線分 $\text{AB}$ の $\text{A}$ の方向への延長上
にある.
説明文
説明文
内分と外分
次の線分 $\text{AB}$ において,次の点を図示せよ.
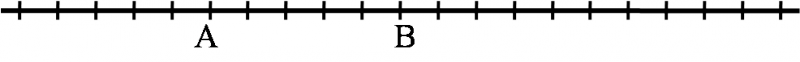
- $\text{AB}$ を $1:4$ に内分する点 $\text{P}$
- $\text{AB}$ を $3:2$ に外分する点 $\text{Q}$
- $\text{AB}$ を $3:2$ に内分する点 $\text{R}$
- $\text{AB}$ を $1:2$ に外分する点 $\text{S}$
