方べきの定理
方べきの定理
方べきの定理
方べきの定理には,主に次の2つがある.
- 1つの円における2つの弦 $\mathrm{AB},\mathrm{CD}$ の交点,またはそれらの延長の交点を $\mathrm{P}$ とすると, \[\mathrm{PA}\cdot\mathrm{PB}=\mathrm{PC}\cdot\mathrm{PD}\]
- 円の外部の点 $\mathrm{P}$ から円に引いた接線の接点を $\mathrm{T}$ とする. $\mathrm{P}$ を通ってこの円と2点 $\mathrm{A},\mathrm{B}$ で交わる直線を引くと, \[\mathrm{PA}\cdot\mathrm{PB}=\mathrm{PT}^2\]
が成り立つ.
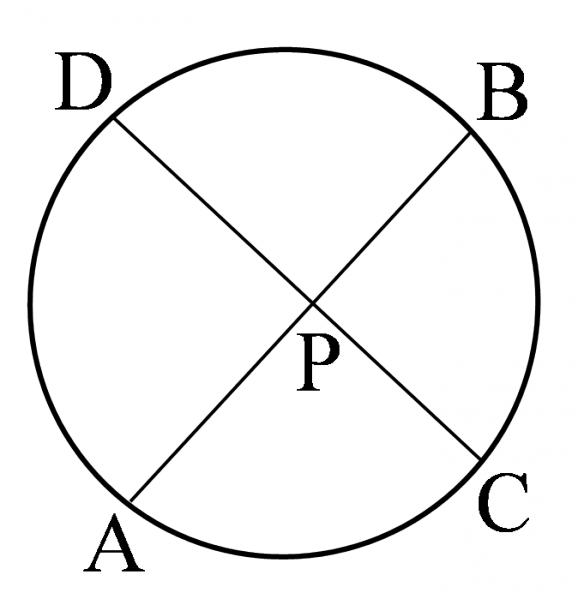

が成り立つ.

方べきの定理
次の図において, $x$ の値を求めよ.ただし,Tは円の接点とする.
- $4\cdot4=8x$ , $\boldsymbol{x=2}$
- $(x+6)\cdot{x}=5\cdot8,x^2+6x-40=0$
- $6\cdot10=x^2$
$x\gt0$ より, $\boldsymbol{x=4}$
$x\gt0$ より, $\boldsymbol{x=2\sqrt{15}}$


