2円の位置関係
2円の位置関係
2円の位置関係は,2円の半径と中心間の距離で決まり,以下の5つの状態がある.
2円の位置関係
2円の半径を $r_1,r_2(r_1\lt r_2)$ ,中心間の距離を $d$ とすると,以下のようになる.
| 2円の図 |  |  |  | |
| 2円の位置関係 | 離れている | 外接している | 交わっている | |
| 2円の共有点の個数 | 0個 | 1個(外接) | 2個 | |
| 2円の中心間の距離 $d$ | $d\gt{r_1+r_2}$ | $d=r_1+r_2$ | $d\lt{r_1+r_2}$ |
| 2円の図 |  |  | |
| 2円の位置関係 | 内接している | 一方が他方を含む | |
| 2円の共有点の個数 | 1個(内接) | 0個 | |
| 2円の中心間の距離 $d$ | $d\gt{r_2-r_1}$ | $d\lt{r_2-r_1}$ |
2円の関係
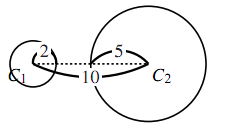
円 $C_1$ は $\text{A}$ を中心とした半径 $2$ の円,円 $C_2$ は $\text{B}$ を中心とした半径 $5$ の円とする.
- $\text{AB}=10$ のとき,円 $C_1$ と $C_2$ はどんな位置関係にあるか.また, $\text{AB}=6$ のとき, $\text{AB}=2$ のときはどうか.
- $C_1$ と $C_2$ が外接するとき線分 $\text{AB}$ の長さを求めよ.また,内接するときはどうか.
- $C_1$ が $C_2$ に含まれるための,線分 $\text{AB}$ の長さの条件を求めよ.
- $\text{AB}=10$ のときは共有点がない
- 外接のときは $\text{AB}=7$ ,内接のときは $\text{AB}=3$ .
- 線分 $\text{AB}$ の長さが,内接するときより短ければよいので, $(0\lt)\boldsymbol{\text{AB}\lt3}$ .
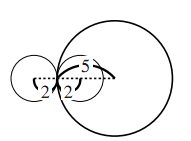
$\text{AB}=6$ のときは2点で交わる
$\text{AB}=2$ のときは円 $C_1$ が円 $C_2$ に含まれている