扇形の弧の長さと面積
無題
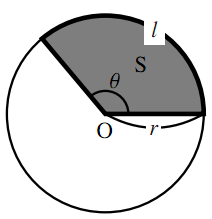
扇形の弧の長さと面積
扇形の弧の長さと面積を,弧度法をもちいて表してみよう.
図のように半径が$r$,中心角が$\theta$の扇形の弧の長さを$l$,面積を$\text{S}$とすると,弧度法の定義より$\theta=\dfrac{l}{r}$だから
\begin{align} \therefore~&l=r\theta \end{align} $\tag{1}\label{ougigatanokononagasatomenseki1}$面積と中心角の比から
\begin{align} \qquad{\text{S}}:\theta=\pi r^2:2\pi \end{align} \begin{align} \therefore~&\text{S}=\dfrac{1}{2}r^2\theta \end{align} $\tag{2}\label{ougigatanokononagasatomenseki2}$以上,$\eqref{ougigatanokononagasatomenseki1}$,$\eqref{ougigatanokononagasatomenseki2}$より,$\text{S}=\dfrac{1}{2}rl$となる.
扇形の弧の長さと面積
無題
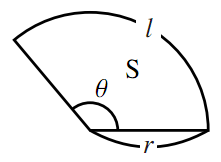
半径が$r$,中心角が$\theta$の扇形の弧の長さを$l$,面積を$\text{S}$とすると
\begin{align} &l=r\theta\\ &\text{S}=\dfrac{1}{2}r^2\theta=\dfrac{1}{2}rl \end{align}である.
吹き出し扇形の弧の長さと面積
無題
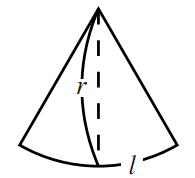
図のように,扇形を,あたかも底辺が$l$,高さが$r$の三角形のように考え, (底辺)$\times$(高さ)$\div 2$から,$\text{S}=\dfrac{1}{2}rl$と覚えておけばよい.
扇形の弧の長さと面積
次のような扇形の弧の長さ$l$と面積$\text{S}$を求めよ.
- 半径が$9$,中心角が$\dfrac{2}{3}\pi$
- 半径が$3$,中心角が$\dfrac{\pi}{5}$
- $l=9\times\dfrac{2}{3}\pi=\boldsymbol{6\pi},$
$\text{S}=\dfrac{1}{2}\times9\times6\pi=\boldsymbol{27\pi}$ - $l=3\times\dfrac{\pi}{5}=\boldsymbol{\dfrac{3}{5}\pi},$
$\text{S}=\dfrac{1}{2}\times3\times\dfrac{3}{5}\pi=\boldsymbol{\dfrac{9}{10}\pi}$