三角関数の定義について

三角関数の定義について

FTEXT 数学Iで学んだ三角比(trigonometric ratio) で扱う角を任意の実数 とすれば，次の三角関数(trigonometric function) の定義となる．

三角関数の定義

無題

無題

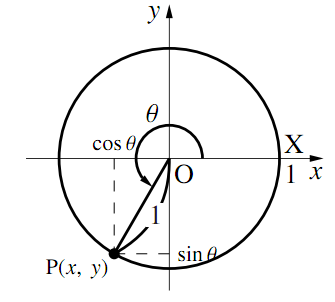
単位円周と動径の交点を$\text{P},\text{X}(1,~0)$とする．

$\angle{\text{POX}}=\theta$($\theta$は任意の実数)とするとき

$\cos\theta = $(動点$\text{P}$の$x$座標)

$\sin\theta = $(動点$\text{P}$の$y$座標)

$\tan\theta =$ (動点$\text{P}$の$y$座標)$/$(動点$\text{P}$の$x$座標)$=$(動径$\text{OP}$の傾き)

とする． ただし，動点$\text{P}$の$x$座標が$0$のとき， つまり$\theta=\dfrac{\pi}{2} +n\pi$($n$は整数) のときは$\tan\theta$は定義されない．

（注） （注）

具体的な例で確認してみよう．

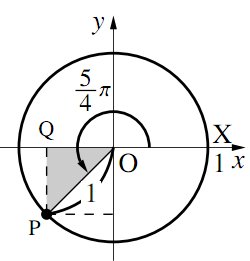
三角関数の定義についての図その１

1)$\theta=\dfrac{5}{4}\pi$のとき

$\triangle{\text{OPQ}}$は$\text{PQ}:\text{QO}:\text{OP}=1:1:\sqrt{2}$の直角三角形である．つまり，$\text{P}\left(-\dfrac{\sqrt{2}}{2},~-\dfrac{\sqrt{2}}{2}\right)$なので

\begin{align} &\cos\dfrac{5}{4}\pi=-\dfrac{\sqrt{2}}{2},~~~\\ &\sin\dfrac{5}{4}\pi=-\dfrac{\sqrt{2}}{2},~~~\\ &\tan\dfrac{5}{4}\pi=1 \end{align}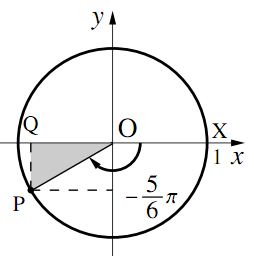
三角関数の定義についての図その２

2)$\theta=-\dfrac{5}{6}\pi$のとき

$\triangle{\text{OPQ}}$は$\text{PQ}:\text{QO}:\text{OP}=1:\sqrt{3}:2$の直角三角形である．つまり，$\text{P}\left(-\dfrac{\sqrt{3}}{2},~-\dfrac{1}{2}\right)$なので

\begin{align} &\cos\left(-\dfrac{5}{6}\pi\right)=-\dfrac{\sqrt{3}}{2},~~~\\ &\sin\left(-\dfrac{5}{6}\pi\right)=-\dfrac{1}{2},~~~\\ &\tan\left(-\dfrac{5}{6}\pi\right)=\dfrac{1}{\sqrt{3}} \end{align}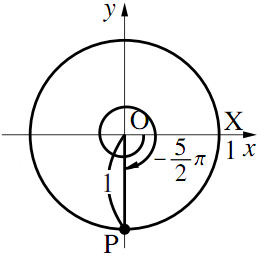
三角関数の定義についての図その３

3)$\theta=-\dfrac{5}{2}\pi$のとき

$-\dfrac{5}{2}\pi=-\dfrac{1}{2}\pi -2\pi$より， $\text{X}$から負の方向へ$-\dfrac{1}{2}\pi$移動した$(0,~-1)$に$\text{P}$があるので

\begin{align} &\cos\left(-\dfrac{5}{2}\pi\right)=0,~\\ &\sin\left(-\dfrac{5}{2}\pi\right)=-1,~\\ &\tan\left(-\dfrac{5}{2}\pi\right) \end{align} は定義できない

$\tan\theta$には次のような意味もあることを理解しておこう．

$\tan\theta$の図形的意味

無題

無題

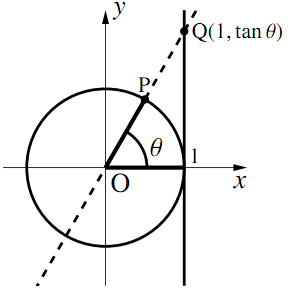
$\tan\theta$の定義は，動径$\text{OP}$の傾きであるが，傾きとは$x$軸方向に$1$増加するときの$y$軸方向の増加量である． そのため，図のように直線$\text{OP}$と直線$x = 1$の交点を$\text{Q}$とすると，$\text{Q}$の$y$座標が$\tan\theta$になる．