$y=ax^2$ のグラフ

まずは、2次関数$y=ax^2+bx+c$において$b=c=0$の場合、つまり \begin{align} y=ax^2 \end{align} のグラフについて考えてみよう。
このグラフについては、中学校で学んだように次のような特徴があった。

$y＝ax^2$ のグラフの特徴

  1. 原点を通り、$y$ 軸に関して対称である。
  2. グラフの $y$ 座標の増減に着目すると
    1. 下に凸なグラフ
      $\boldsymbol{a\gt0}$ のとき
      • $y\geqq0$ の範囲にある。
      • $x$ の増加に対し
        • $x\lt0$ では $y$ は減少する
        • $x\gt0$ では $y$ は増加する
      このグラフのようにいったん下がってから上がるグラフのことを、下に凸とつ (convex) なグラフという。
    2. 上に凸なグラフ
      $\boldsymbol{a\lt0}$ のとき
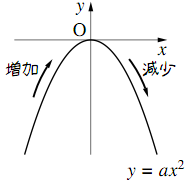
      • $y\leqq0$ の範囲にある。
      • $x$ の増加に対し
        • $x\lt0$ では $y$ は増加する
        • $x\gt0$ では $y$ は減少する
      このグラフのようにいったん上がってから下がるグラフのことを、上に凸 なグラフという。

放物線の図

放物線の図

一般に、2次関数のグラフにあらわれる曲線のことを放物線ほうぶつせん (parabola) という。この名前は、空中に物を放り投げたときにできる軌跡きせきに由来する。

放物線は必ず対称軸をもち、この対称軸のことを単に軸 (axis) といい、この軸と放物線の交点のことを頂点 (vertex) という。