空間の正射影ベクトルの内積での表し方

平面ベクトルの場合と同じように，空間ベクトルでも同様な形で，正射影ベク トルを内積で表すことができる．

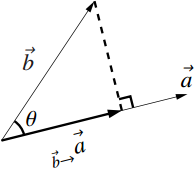
$\vec{b}$ の$\vec{a}$ への正射影ベクトル$_{\vec{b}\rightarrow}\vec{a}$ は

\begin{align} _{\vec{b}\rightarrow}\vec{a} &= \dfrac{\left|\vec{b}\right| \cos \theta}{\left|\vec{a}\right|}\vec{a}\\ &=\dfrac{\left|\vec{a}\right|\left|\vec{b}\right| \cos \theta}{\left|\vec{a}\right|^2}\vec{a}\\ &\because 分母分子に\left|\vec{a}\right| をかけた\\ &=\dfrac{\vec{a} \cdot \vec{b}}{\left|\vec{a}\right|^2}\vec{a}\\ &\because \vec{a} \cdot \vec{b} = \left|\vec{a}\right|\left|\vec{b}\right| \cos \theta \end{align}

と表すことができる．